从经典解法赏析到模型结论应用

徐羽

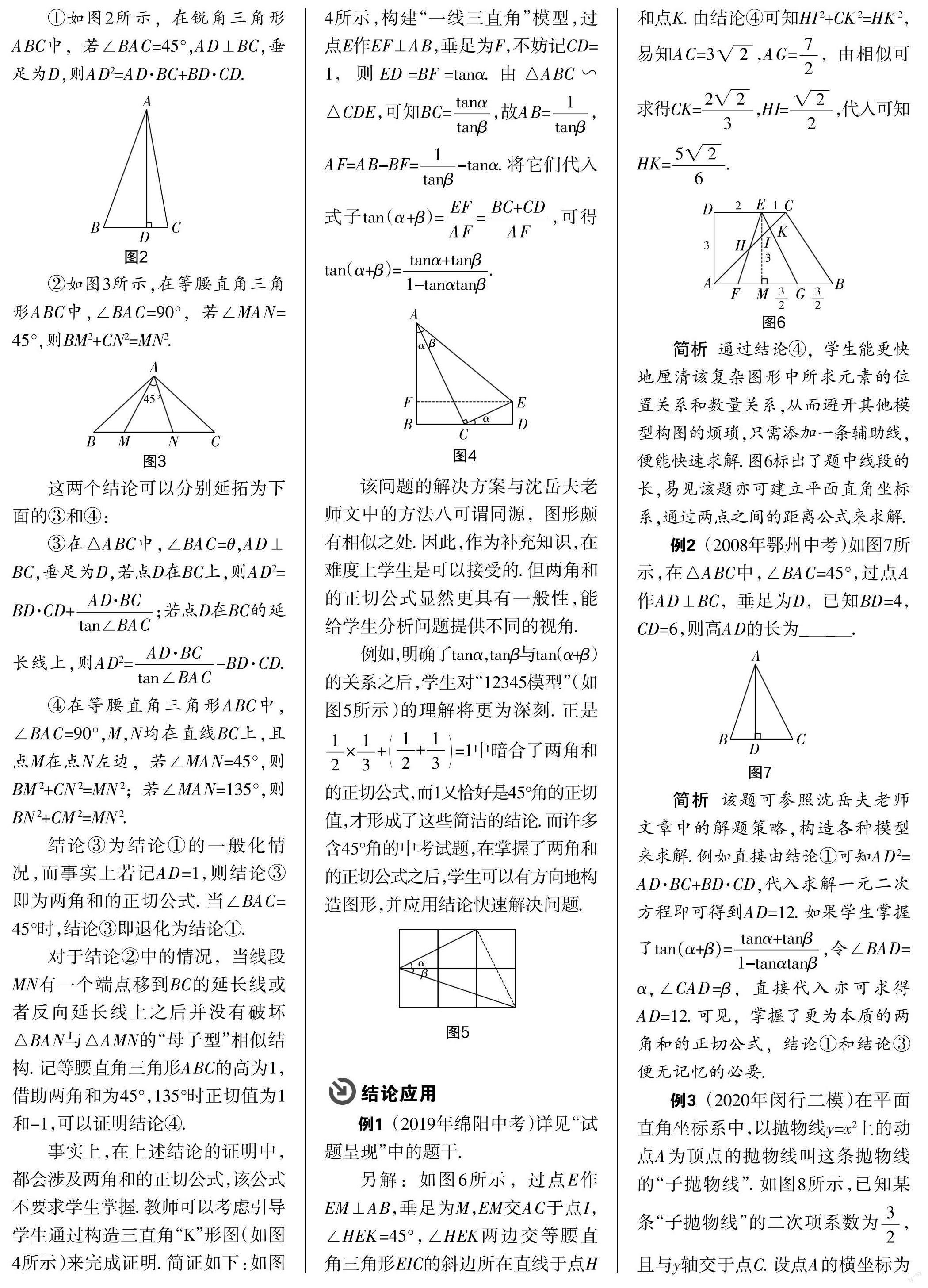
［摘  要］ 简洁明了的代数原理或结论是助推几何学习的利器. 中考试题的经典解法值得師生反复揣摩与品味. 对于中考试题，教师除了要引导学生观察题目表象，探求解题方法之外，还应阐明模型的代数内核，使学生在把握问题本质的基础上能更好地使用模型、应用结论解决问题.

［关键词］ 中考试题；45°角；模型

数学家哈尔莫斯说过，问题是数学的心脏. “以问题引领学生体会数学思想，汲取数学智慧”是教学的重要方式之一. 尤其是一些中考试题，在一线师生的探究、钻研下，呈现的多种经典解法值得我们反复揣摩与品味. 奇文共欣赏，疑义相与析. 解决疑惑之后，对解法进行提炼，对结论进行推广与应用，把握模型所蕴含的代数内核，能促进学生深度学习，从而提高学生的逻辑推理与数学运算等核心素养.

结语

初中阶段的几何学习分别从演绎证明、运动变化、量化分析三个方面来研究图形的基本性质和图形间的相互关系. 演绎证明、运动变化、量化分析相当于研究基本图形的三个不同角度，既相互独立又相互交织［2］. 教师应当提纲挈领，在特定几何问题上给学生提供代数视角，以求更好地融会贯通. 通过几何分析与代数解读两相对照，学生可以更好地把握问题本质，从而提高构造几何模型的能力，增加代数公式的应用方法.

我国著名数学家苏步青先生曾多次鼓励数学教育工作者多用高观点来解决初等数学问题. 正所谓“不畏浮云遮望眼，自缘身在最高层”. 教师如果可以适时地引导学生提炼更高的观点，那问题中原本复杂的条件、隐藏的信息在学生眼中便会变得简洁和清晰. 学生深度学习之后，基于代数公式的视角，也一定能更好地利用几何知识解决问题.回看解决问题的方法，也必然会有“一览众山小”的畅快.

中学时期涉及的一些几何定理，如勾股定理、托勒密定理、婆罗摩笈多定理，其巧妙绝伦的几何推导与证明会给学生的思维带来冲击与享受，而定理的简洁、明快更会让学生体会到数学的简洁之美. 毫无疑问，运用定理解决问题时，学生更多地是直接应用结论而非借鉴相应定理的证明思路，对日常教学中总结的经典结论亦是如此. 一题多解的讲评赏析，多种知识交叉比对，能极大地提高学生分析问题和解决问题的能力. 除此之外，对于问题中的一些结论，适时地总结延拓，去粗取精，将表象背后的代数内核挖掘出来，将有助于学生分析问题，“拨云见日”地找到解决方法，从而为他们的数学学习助力.

参考文献：

［1］沈岳夫. 多元的视角  多彩的解法——对一道含45°角中考选择题的多角度思考［J］. 数学教学，2021（09）：30-35.

［2］陈莉红，曹经富. 2021年中考“图形的性质”专题命题分析［J］. 中国数学教育，2022（z1）：68-78+96.