逆向架构理解

【摘 要】 对认知与提问的复杂性加以思考，提出被动灌输与自主建构的两类学生解决问题时采用的不同思维方式，利用案例说明如何以“慢思维”艺术的方式设计问题，防止课堂中的被动“灌输”陷阱；对比研究PBL与UbD教学模式，以案例说明怎样围绕问题设计框架，精细化教学流程，以追求最优效果的教学过程；從教学活动设计与思维习惯培养两个方面思考如何提升课堂问题参与率.

【关键词】 核心问题；UbD逆向设计；PBL教学法

0 引言

袁隆平院士说过：“我最不喜欢数学，不清楚为什么负负相乘得正数，就去问老师，老师说‘你记住就行了.我由此得出结论，数学不讲理，于是就不再理会，对数学兴趣不大，成绩也不好．”无独有偶，有同样经历一样不理解“负负得正”的还有美国诗人奥登、法国著名作家司汤达．我们直接把定理抛给学生，然后刷题开始练，这是一个严重的问题，也是数学教学的悲哀．即使再简单的公式也需经历长时间的探究才能形成．作为教师，应当承认数学是难以理解的．数学教学应是一个思维建构的精细化设计，等待并精心呵护学生的问题共鸣，并以“慢思维”艺术为概念和知识赋予的新意义．

1 问题设计决定学生的思维方式

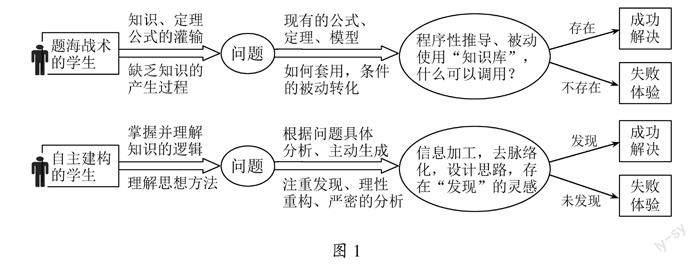
在双减背景下，我们依然需要关注学习成绩，在教研培训中不断被奉告：知识不能被动“灌输”．但上课中的探究依然如快餐般被动植入，我们精简知识的建构过程，将教学的侧重点放在如何解题上，这样的做法在短期之内确实有效．这类学生在中考可能获得不错的成绩，但在初中毕业之后的数学乃至理科的学习中并不如意．抛弃了知识的产生过程、问题的发现过程，培养的学生在解决问题时思维方式是不一致的（图1）.

面对以核心素养为导向的中高考评价，教师如果没有改变教学的方向，那么学生“复习用不上”“刷题不灵验”之类的抱怨将屡见不鲜．之后的命题将更多的是“意料之外”（没做过、没刷过），“情理之中”（都是新课标中“内容标准”所要求），体现通性通法、考察思维方法、脱离套路与模式将是命题的主方向．由此可见，学生做到掌握知识学习过程中的通性通法、理解并灵活运用思想方法、形成解决新问题的能力，才能在考试乃至后续学习以及在社会生活中适应、胜任以致自我提升．

2 “慢思维”艺术防止知识点“灌输”陷阱

教师往往难以设身处地的体会学生的理解困境，需要以“慢思维”艺术的方式精心设计问题并引导学生自主建构.那么如何提问，才能促使学生建立概念、意义的合理化表征与结构，改变问题设计中发现性、创新性不足的弊端，让学生由知识的被动灌输对象转为意义建构的主体．谨此，引入两个教学案例进行分析，选择最基础且更容易忽视的章节也许更能说明问题.

“有理数的减法”案例1

温故知新：7道加法练习题．（复习加法法则）

新课：一周温度变化情况表，提问每一天的温差（通过温差，引入减法运算）．星期三最高温度3℃，最低-3℃．

①师：星期三的温差需要怎么运算．生：减法．

②师：如何运算？怎么列式呢？生：3-（-3）．

③师：3-（-3）究竟得多少呢？借助温度计得到3℃到-3℃的温差是？生：6.

④师：小学时已经知道减法是加法的逆运算，那么3+（+3）得几？生：6.

⑤师：从这个层面上我们得到3-（-3）=3+（+3）（最近发展区）那么大家是否可以得到一个大胆的猜想，也就是说？（分析：以上学生回答，均为全班齐答．教师此处停顿，未得到全班齐答．提问生A）生A：括号前面是减号，括号里的数应该变号．

⑥师：还可以怎么说？（提问生B）．生B：减去一个数等于加上这个数的相反数．

任务单：（独立阅读、理解教材内容，在小组内讨论交流．）1.完成课本探究部分；2.归纳减法法则；3.谈谈你对法则的理解．小组讨论后：

⑦师：在大量的运算后，你们发现什么？（教师手指板书：9-（-8）=9+（+8），学生齐答：减法运算律．）

⑧师：请你用自己的语言归纳一下减法法则．生C分别用文字语言和符号语言归纳．

⑨师：对减法法则你有怎样的认识？

生D：有理数减法法则可以让我们简便运算．生E：有理数减法法则可以让我们把减法运算转化为加法运算．生F：有理数减法法则需要注意符号．

生G：还注意“两变”1.减号；2.相反数……

调查研究中，绝大多数课例均选择温度计作为情境引入，这与教材不谋而合．课例选择让学生通过3-（-3）和3+（+3）相等的事实，合情推理得出减法法则．本节课的核心应该是学生对于减法法则合理性的思考、运算法则的产生、运算律的理解与运用，在问答⑤中，并未给出足够的课堂留白，这样的设计方式难以从本质上让学生分析知识与定理（运算律）的内在逻辑．在生A的回答后，教师应该顺着生A的回答，小步子分解，引导学生自己总结，这也是本节课的弊病．

⑥中生B回答复述课本中的运算律，同伴的认知未能有效转化为全班学生的群体认知．核心知识点的复杂性思考、扩大并深化认知无法达成，有效思考的缺失导致课例无法脱离知识点“灌输”陷阱．但这节课亮点在讨论环节的有效性，学生在学案的引导下触发对运算律运用的深度理解（问答⑧至⑨）．从这个角度成功裨补阙漏，就教学效果而言，本节课是成功的．

“有理数的减法”案例2

①师：本节课我们要学习有理数的减法运算．那么怎么运算呢？（教师引入课题）

生（齐答）：减去一个数等于加上这个数的相反数．（教师意外于学生提前预习、直入正题）

②师：那么，为什么减去一个数等于加上这个数的相反数（学生陷入沉默）．我知道，你们都清楚书上的重点在黑体字的部分．但为什么呢？这个运算律是怎么得到的？

生A：（-8）-（-3）=-5，（-8）+（+3）=-5，所以（-8）-（-3）=（-8）+（+3）；（教师同步板书）

③师：确实，大家能理解吗？通过观察，确实能发现这个运算律是合理的．你能举其他类似的例子吗？有不成立的例子吗？（学生举例，教师板书，学生未举出反例）

④师：很好，大家关注的这个运算律的发现过程．无法举出反例，是合理的．这个说明也是书本中的，你能找出其他书本没有的理由或依据吗？

⑤生B：从数轴的角度，加上正数表示向右移动，那么（-8）-（-3）表示代表-8的点向左移动-3个单位，即向右移动+3个单位．可以说明减法运算律．生C：减法表示两个数之间的距离，那么（-8）-（-3）表示-8与-3间的距离，等于-3与-8的距离，通过数轴也可以得到.教师提问学生4～5人，慢慢培育发现的火花，利用学生的问题与新观点生成问题．当学生有特殊发现后，进行点评，力求让新发现的个体认知转化为全班学生的共同理解．教师设置开放问题，启发学生深入思考，让全班学生理解运算律，抓住核心知识点提问，让学生从分析数学问题到生成数学问题，教师再从学生的观点中提炼生成性问题并继续引导．

3 后建构主义的问题设计与教学模式分析

3.1 从PBL到UbD

从以上案例可以看出，数学课堂有效与否离不开问题设计，那么如何更好地架构并设计问题？这方面教育理论并不少，从建构主义到近年来“基于问题的学习”（PBL：Problem-Based Learning），再到“追求理解的设计”（UbD：Understanding by Design），以问题为基础来开展学习和教学的过程成为教学改革的基本思路．

PBL以问题导学，而UbD在于确定核心（大概念与核心问题）并围绕其设计问题框架，精细化教学流程．PBL中的问题可以指代任务与项目，这与UbD的核心问题不谋而合．两者研究的都是能促进学生产生怀疑、主动探究理解意义，并产生激发学习迁移的问题情境．将当下国外主流的两种教学模式进行明确对比之后，我们易于找准教育改革的关键所在，重点在于教学实践中对问题做出精细化研究与设计，以确保教学取得成功．

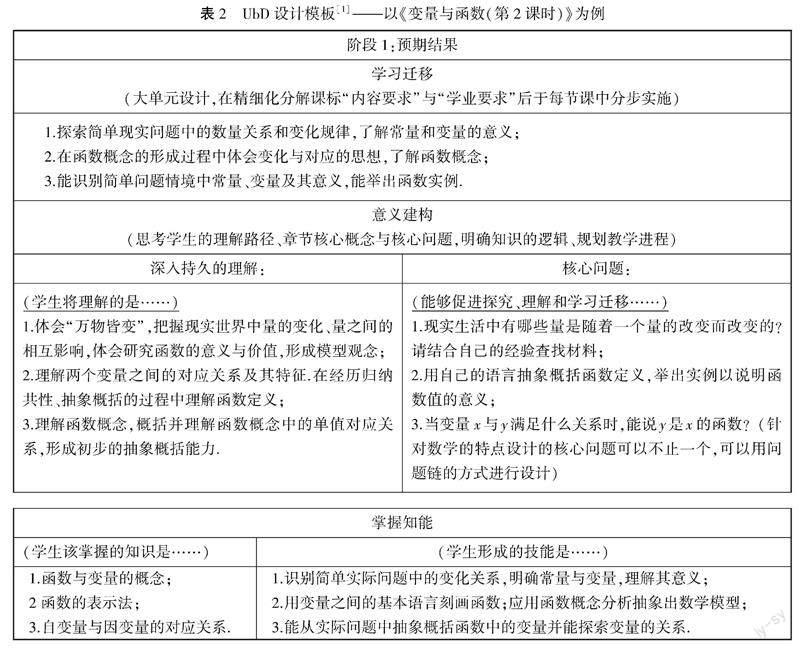
3.2 追求理解的逆向问题设计

“阶段2：明确评估证据与核心任务”：重点在于前置教学评价，这样的评价可以是教学量表、量规、表现型任务、基于课标分解的练习与习题等．

“阶段3：学习活动的设计”：在达成前两个阶段教学预期、教学评价后再思考教学的过程，防止灌输式教学．

UbD逆向设计的价值在于引导教师于设计前思考深度“理解”的要素、达成“理解”的有效路径、如何进行有意义的学习、挖掘核心素养下的教学关键点、提炼大概念与核心问题等．在设计的伊始思考学习达到的目的以及相应评价，指导教师关注教学期望，进而通过框架化的设计流程，有效转变路径，“以始为终”地追求最优效果的教学过程．

4 思维参与率的提高在于“预测”的听课方式

有效的教学源自于设计，精心设计的问题却收效甚微，还忽略了什么因素呢？ （答疑片段，师：这个部分上课已经讲过、提问过，我们也探究了，你怎么还没掌握呢？ 生 Ｅ：老师您没有提问我呀．师：难道没问过，你就不用思考吗？）忽略了学生思考课堂问题的参与率！我们过于专注知识的传授，常常忽视师生间知识构建的完整循环．提升课堂参与率，需要有适切的、指向明确、有价值的课堂活动．活动意义在于达成学生与同伴之间的知识交互．

图2如何更好设计活动？（图2为课堂中的知识流向图，箭头的方向表示知识的流向，教师可以在箭头的位置设计相应的课堂活动）在关注知识流向中明确地、有针对性地设计课堂活动，提升学生参与率.（图3为活动/任务的设计案例）不同学生的问题是不一样的．活动设计模型能引导我们通过知识传播的路径根据自己教学的侧重点选择有效的教学策略，把控知識产生的过程．通过反思知识路径，使自己设计的活动更有意义，也使知识在学生、教师与同伴间达成完整的知识交互与建构，促进深度学习的发生．

学生没有真正参与课堂问题并触发有效思维、人云亦云的无效回答，无法将同伴与教师的认知转化为自身的学习体验，这直接决定课堂的教学效果．除了教师的领导力、课堂环境、学习模式、教学资源等因素外，学生个体的思维习惯是教学的关键因素．即使在简单的“齐答”中也有滥竽充数的学生．应该让学生形成有效参与数学课堂的能力．这一切的前提是预测（像与老师对弈一样听课）：于教师将问未问前预测说什么，于同学将答而未答时预测答什么，于教师将写未写前预测写什么等．在预测错时及时纠偏：思考结论的正确性、证明过程运用的方法、得出结果的依据、教师与数学家的思维逻辑、能否进一步抽象、是否有其他性质等．数学学习在于思维，未培养学生这样的课堂思维习惯，难以引发适切的、针对问题的有效思考．

参考文献

[1]格兰特·威金斯，杰伊·麦克泰格.追求理解的教学设计[M].闫寒冰，宋雪莲，赖平，译.上海：华东师范大学出版社，2017.

作者简介 罗逸晖（1988—），男，福建泉州人，福建省泉州市学科带头人，泉州市骨干教师，泉州市第二批教育“领航团队”成员;主要从事课标、课程与教学论研究、中考命题研究；发表论文10余篇，主持省、市级、区级多项课题.

基金项目 福建省教育科学“十四五”规划2021年度课题“基于UbD下中学生数学核心素养提升的问题设计研究”（FJJKZX21-706）.