加强应用意识培养 提升学生核心素养

李树臣 张娟萍

【摘 要】 《义务教育数学课程标准（2022年版）》首次提出数学核心素养的概念，把核心素养高度概括为“三会”.核心素养在三个学段的表现不同，都有应用意识和创新意识.应用意识是核心素养中的重要体现之一，教学中加强应用意识培养是培养和提高学生核心素养的需要.以函数主题为例，在对函数的认识、函数概念的形成以及建立各种函数模型解决实际问题的过程中都能提高学生的应用意识.

【关键词】 核心素养;应用意识;函数主题

《义务教育数学课程标准（2022年版）》（以下简称《课标（2022年版）》）把“应用意识”作为小学、初中、高中数学“跨学科”的素养表现，并且在“课程性质”中用“数学的应用渗透到现代社会的各个方面，直接为社会创造价值，推动社会生产力的发展” [1] 进一步肯定了培养学生应用意识的重要性.

本文首先谈谈对“应用意识”的理解，然后结合案例说明培养应用意识的主要途径.

1 培养学生应用意识具有重要的意义

1.1 应用意识是数学核心素养的重要组成部分

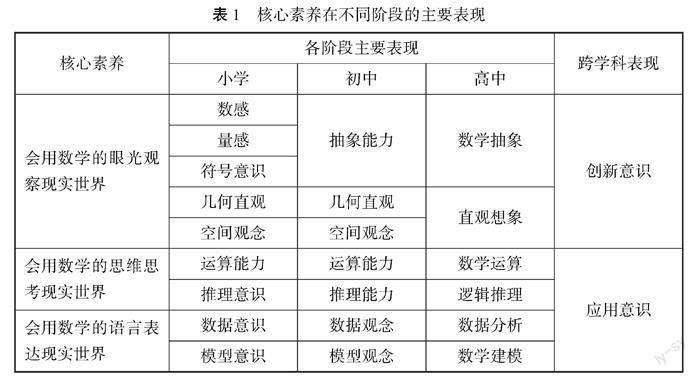
数学学科核心素养包括：数学抽象、数学推理、数学建模、直观想象、数学运算和数据分析 [2] .目前，我国的数学核心素养概念体系基本建立，如表1 [3] .

从表1可以看出，三个学段（小学数学、初中数学、高中数学）核心素养都是“三会”，都有“应用意识”与“创新意识”，但核心素养具体体现的“称谓”和数量不同.“应用意识”与“创新意识”着重在“跨学科表现”.

应用意识已经超出了知识与认知的范畴，也包含了情感态度价值观的成分，是整个中小学数学课程与教学的基本要求 [3]82 .

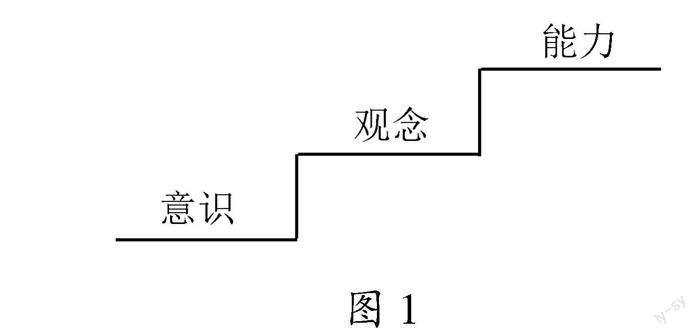
初中学段核心素养的具体表现有“意识”“观念”“能力”之分.“意识”“观念”“能力”三个概念是有层次的：处于最底层的是意识，中间层次是观念，最高层次的是能力 [4] ，如图1所示.

数学意识是指学生在思考问题时，能自觉地从数学的角度观察问题、分析问题，并利用数学的知识、方法解释或解决问题的一种思维习惯；数学观念是指运用数学的觀点、方法去观察、认识问题的自觉意识和思维方式；数学能力是一种特殊的能力，它是与数学活动相适应，保证数学活动顺利完成所必须具备的心理条件.

1.2 重视应用意识培养体现了课标的要求

《课标（2022年版）》共提及“应用意识”58次，详细阐述为“应用意识主要是指有意识地利用数学的概念、原理和方法解释现实世界中的现象与规律，解决现实世界中的问题.能够感悟现实生活中蕴含着大量的与数量和图形有关的问题，可以用数学的方法予以解决；初步了解数学作为一种通用的科学语言在其他学科中的应用，通过跨学科主题学习建立不同学科之间的联系.应用意识有助于用学过的知识和方法解决简单的实际问题，养成理论联系实际的习惯，发展实践能力” [1]10 .

数学应用有两个维度：一是由实际问题建立数学模型，形成数学问题（即实际问题数学化）；二是应用数学知识、数学方法和数学思想解决数学问题（即解数学应用题）.

20世纪下半叶以来，数学最大的进步是应用，正如姜伯驹所说：“谁用的好，谁就赢了.”当今世界已经全面进入信息社会，随着高新技术的飞速发展，人们越来越感受到“数学不仅是一门科学，更是一门被普遍应用的技术”.可以说数学几乎渗透到了每一个科学领域及人们生活的方方面面，得到了空前的应用.在这样的背景下，我们的数学教育应通过数学知识的传授，培养和发展学生的应用意识，让学生形成在这个信息世界里生存的本领.

根据《课标（2022年版）》的要求，在初中阶段需要结合课程内容的学习，培养学生的应用意识.如果学生的数学应用意识不强，当他们遇到实际问题时，就不能从数学的角度去进行有效地思考，就不能很好地运用数学知识、数学思想方法去解决，培养学生的“四能”就成为一句空话.培养学生的数学应用意识是学生学好数学、运用数学的前提.

1.3 应用意识培养符合学生的学习需要

由生活实际引入新知有利于学生体会数学知识的应用价值，体现学生数学学习的过程和方法领悟过程.应用意识培养是用数学解决实际问题，最终实现知识对生活的应用.数学在经济、医学、社会、建筑、信息技术等方面应用广泛，培养应用意识是学生学习数学的重要目标.

2 培养数学应用意识的基本策略

《课标（2022年版）》将“课程内容”划分为“数与代数”“图形与几何”“统计与概率”和“综合与实践”四个领域，并按照“领域→主题→具体内容”三个层次呈现了具体课程内容.在初中学段，“数与代数”领域分为三个主题，“函数”主题是其中之一.

“函数”主题下有函数的概念、一次函数（正比例函数）、二次函数、反比例函数.函数内容和函数思想贯穿于数学理论和实际应用的每一个场合.它是有效地表示、处理、交流和传递信息的有力工具，是探讨事物发展规律、预测事物发展方向的重要手段.

2.1 结合函数知识学习让学生加深对数学应用的认识

我们的生活离不开函数：

（1）函数与每个人都息息相关.如一个人的身高、体重等都是时间（年龄）的函数；

（2）函数与生活密切相关.如电话费、煤气费等都是时间的函数；

（3）许多科学只有用函数才能表达清楚.如物理学中的自由落体运动、生物学中的细胞繁殖速度等也是时间的函数；

（4）生产生活中的一些问题只有用函数的知识才能统筹规划.如生产成本的核算、生产工效的提高等都是相应自变量的函数.

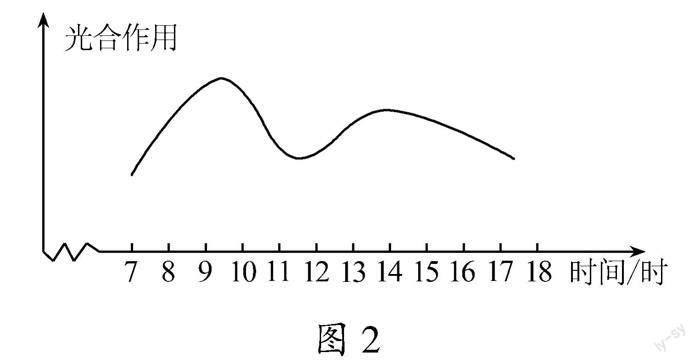
案例1 什么时间光合作用最强？

光合作用是指绿色植物通过叶绿素，利用光能把二氧化碳和水转化成储存能量的有机物，并释放出氧气的过程.图2是夏季的白天7—18时一般绿色植物的光合作用强度与时间之间的关系图象，分析图象回答问题：

（1）大約几时的光合作用最强？

（2）大约几时的光合作用最弱？

（3）分析光合作用的强度随时间变化的趋势，根据实际情况你认为如果每天锻炼身体，何时为最佳锻炼时间？

设计意图 在学生学习了函数的三种表示方法后，我们按照《课标（2022年版）》提出的“选材应当尽可能地贴近学生的现实，以利于学生经历从现实情境中抽象出数学知识与方法的过程，发展抽象能力、推理能力等”的要求，从生物学角度出发设计了本例.目的有二：

（1）让学生学会“读图”，正确理解和使用数学语言.数学语言有文字语言、符号语言和图形语言三种形式，本题中的信息是用“图形语言”给出的，学习数学必须会“读图”，从图中获取有价值的信息；

（2）加深学生对“数学来源于生活”的认识，感悟到数学是学习物理、化学、生物等学科的基础.这些学科中的许多知识都要用到数学（函数）的知识才能解决.本题就是引导学生利用函数图象的知识解答与生物学科中的有关问题.

这就客观要求我们在选取素材、设计教学情境时，尽量把与之相关的其他学科知识融合进来，以增强学生应用数学知识解决问题的能力.

2.2 函数概念来源于生活实际

数学中充满许多大小不同的“三步曲”，首先，它把现实世界问题通过“水平数学化”转化为数学问题；然后，通过“垂直数学化”研究和解决数学内部问题；最后，借助数学概念和原理解决现实问题 [5] .

数学概念是重要的基础知识，它反映了事物包括数量关系、空间形式在内的结构关系的本质属性.对于数学概念的教学一定要展示数学概念的发生发展过程，在过程中揭示其内涵与外延，再现基本结论的发现过程，理清知识点之间的逻辑关系.

数学概念都有一定的“背景”，在函数主题中，函数的概念以及各种具体函数的概念，在教学中，都要从生活实际出发，设计好“背景问题”，以此引导学生经历概念的建立过程，让学生感知到函数概念都是为了解决数学问题，特别是生活中的实际问题而产生的.

案例2 反比例函概念的建立过程.

为引导学生经历反比例函数概念的形成过程，我们提出下面问题，让学生进行思考、交流等活动：

（1）时代中学要修建一个面积为84m 2 的矩形花圃，则矩形的宽y（m）与长x（m）之间的函数表达式为；

（2）甲、乙两地相距240km，一辆汽车从甲地驶往乙地.汽车行驶的时间t（h）与汽车的平均速度v（km/h）之间的函数表达式为；

（3）某高铁列车行驶在轨道上时，若地面受轨道板的压力为10 7 N，轨道板的底面积S（m 2 ）与轨道板对地面的压强P（Pa）之间有怎样的关系？

（4）请观察上面三个问题中的函数表达式在形式上具有什么共同特征？

设计意图 为了引出反比例函数的概念，让学生“亲身”感悟到为了解决实际问题，需要引入一类新的函数——反比例函数.我们选取了三个问题，前两个问题来源于现实生活，第三个问题以“高铁”为背景，属于物理学科.学生通过对这三个问题的思考，分别得到了三个函数表达式，y=84x；t=240v；P= 10 7S.通过对第四个问题的观察、交流发现，根据三个问题情境列出的函数表达式在形式上的共同特征：都具有y=kx（k≠0）的形式，从而给出反比例函数的意义.

数学中的概念本身都是一些典型的模型，引导学生经历这些模型的产生过程，在过程中掌握概念，理解概念来自于生活，有助于培养学生的应用意识.

2.3 利用函数解决生活中的问题

著名数学教育家弗赖登塔尔在谈到数学应用时，曾指出“应从两个方面来理解数学应用：既要重视从实际问题中提取数学概念和原理，又要重视用数学概念与原理反过来处理实际问题”.

数学概念的建立过程，反映了从现实到数学的数学化过程，从数学到现实的例子比比皆是.数学建模也是数学化的过程，是数学应用的一个组成部分.《标准（2022年版）》把模型观念作为初中阶段核心素养的表现之一，这种观念是在建立概念模型特别是应用模型解决问题的过程中逐渐形成的.

“函数”主题的学习主要围绕“函数概念—图象性质—实际应用”展开的，在“函数概念”学习阶段以及“实际应用”阶段，都离不开“实际问题”，这是培养学生应用意识的大好机会.

案例3 活动板房中的问题（青岛市2020中考题）.

某公司生产A型活动板房成本是每个425元．图3①表示A型活动板房的一面墙，它由长方形和抛物线构成，长方形的长AD=4m，宽AB=3m，抛物线的最高点E到BC的距离为4m．

（1）按如图3①所示的直角坐标系，抛物线可以用y=kx 2 +c（k≠0）表示，求该抛物线的函数表达式；

（2）现将A型活动板房改造为B型活动板房．如图3②，在抛物线与AD之间的区域内加装一扇长方形窗户FGMN，点G，M在AD上，点N，F在抛物线上，窗户的成本为50元/m 2 ．已知GM=2m，求每个B型活动板房的成本是多少？（每个B型活动板房的成本=每个A型活动板房的成本+一扇窗户FGMN的成本）；

（3）根据市场调查，以单价650元销售（2）中的B型活动板房，每月能售出100个，而单价每降低10元，每月能多售出20个.公司每月最多能生产160个B型活动板房.不考虑其他因素，公司将销售单价n（元）定为多少时，每月销售B型活动板房所获利润w（元）最大？最大利润是多少？

析解 （1）把D（2，0），E（0，1）代入y=kx 2 +c可求出k，c的值，得函数表达式为y=-14x 2 +1.

（2）由题意可知只要求出FGMN的面积即可，需要求出N点的纵坐标，把x=1代入y=-14x 2 +1得y=34，所以N（1，34）.所以S 四边形FGMN =GM×MN=2×34=32（m 2 ），每个B型活动板的成本为425+32×50=500（元）.

（3）根据题意可得w=（n-500）（100+20×650－n10）=-2（n-600） 2 +20000.

因为一个月最多生产160个，所以100+20×650－n10≤160，解得n≥620.

因为-2＜0，所以n≥620时，w随n的增大而减小，所以当n=620时，w 最大 =19200元．

设计意图 本题以“活动板房”为背景，设计了三个小题.对于第（1）问，只要从图3②中得到D（2，0），E（0，1）的坐标，然后将其代入y=kx 2 +c即可.对于第（2）求每个B型活动板房的成本价时，根据题目给出的计算方式（每个B型活动板房的成本=每个A型活动板房的成本+一扇窗户FGMN的成本）可以发现求出FGMN的面积是关键.解答问题（3）的关键是根据“每月销售B型活动板房所获利润=每件B型活动板房的利润×每月B型活动板房的销量”建立函数模型w=（n-500）（100+20×650－n10），并且根据“每月最多能生产160个”得到n的取值范围.

本题主要考查了学生对二次函数性质的理解和运用情况，解题的前提是从图中获取有关的信息，熟练运用待定系数法，灵活利用二次函数的性质.在学生学习了二次函数的性质后，可以作为课堂练习用，以不断提高学生的问题解决能力.

函数是刻画变量之间相互依赖关系的数学模型，是《课标（2022年版）》界定的“数与代数”领域中的重要且“抽象”的数学概念之一.学生在掌握了函数有关知识的基础上，依次研究了一次函数（含正比例函数）、反比例函数和二次函数的图象与性质，通过建立函数模型解决实际问题的练习后，能形成对“函数”的优化认知，并且利用“函数”把前面学习过的“数与式”“方程与不等式”两个主题进行深度“融合”，熟练掌握“数与代数”领域的基础知识，形成了利用“代数”载体解决问题的能力，提高了应用意识，实现了《课标（2022年版）》确定的课程目标和学习目标.参考文献

[1]中华人民共和国教育部.义务教育数学课程标准（2022年版）[M].北京：北京师范大学出版社，2022.5.

[2]中華人民共和国教育部.普通高中数学课程标准（2017年版）[M].北京：人民教育出版社，2018.4.

[3]史宁中，曹一鸣.义务教育数学课程课标（2022年版）解读[M].北京：北京师范大学出版社，2022.8.

[4]李树臣，吕春霞.正确理解创新意识，培养学生核心素养——兼谈培养学生创新意识的主要途径[J].中学数学杂志，2023（02）：2-5.

[5]李昌官.基于核心素养的数学单元教学[J].中国数学教育（高中版），2018（05）：3-6.

作者简介 李树臣（1962—），男，山东沂南人，中学正高级教师;临沂大学学生学业导师，山东省教育科研先进个人，山东省创新教育先进个人;三次获山东省省级教学成果奖;全国义务教育初中数学教材（青岛版）核心作者，中国人民大学《复印报刊资料·初中数学教与学》编委，湖北大学《中学数学》特约编委，《山东教育》特约记者.张娟萍（1972—），女，浙江杭州人，中学高级教师，浙江省特级教师，国家心理咨询师;获浙江省基础教育成果二等奖，参加编写浙教版《义务教育教科书》，出版《高阶思维》《高阶能力》等专著.