儿童数学教育视角下的“应用意识”培养

张秋爽

【摘 要】数学应用意识是《义务教育数学课程标准（2011年版）》提出的十个核心词之一。寻找生活原型，帮助学生建构数学概念，感受数学的应用价值；逐步形成模型思想，做到举一反三，能解决新情境的实际问题，进一步加深对数学概念、规律的理解，用数学的知识解释生活中的现象，体会数学和生活的联系、数学和其他学科之间的联系、数学知识之间的内在联系，积累学生的思考经验，提升学生的应用能力。

【关键词】生活原型 应用意识 数学模型

《义务教育数学课程标准（2011年版）》中明确提出“应用意识”这一核心概念，认为应用意识有两个方面的含义：一方面有意识利用数学的概念、原理和方法解释现实世界中的现象，解决现实世界中的问题；另一方面，认识到现实生活中蕴含着大量与数量和图形有关的问题，这些问题可以抽象成数学问题，用数学的方法予以解决。在整个数学教育的过程中都应该培养学生的应用意识，综合实践活动是培养应用意识很好的载体。

因此，在数学教育中培养学生的应用意识，要从密切“数学”与“生活”的联系入手。教师通过改进课堂教学设计，架设学生“知识世界”与“生活世界”之间的桥梁，来重建学生的生活世界。只有当数学不再板起面孔，而是与学生生活实际更贴近的时候，学生才会产生学习的兴趣，才会进入数学学习的角色，才能学懂数学，真正感受和体验到数学的魅力与价值，增进对数学的理解和应用数学的信心。

一、寻找生活原型，建构数学概念，感受数学的应用价值

小学数学中大部分学习内容都可以在生活中找到原型。基于儿童的心理发展特点，他们的学习带有浓厚的情绪色彩，对熟悉的生活情境，感到亲切、有兴趣，我们在教学中应尽可能从学生的生活中提取数学学习的素材，使他们感受到课堂上学习的数学知识来自于生活，感知数学学习的价值，激发他们学习数学的兴趣。

六年级学习“比的意义”，教材中首先借助对国旗长与宽之间关系的探讨，使学生初步感受同类量的比。接下来又借助有关神舟5号飞船的飞行时间和路程来感受不同类量的比，最终揭示比的意义，认识比的各部分名称，学会求比值的方法。笔者设计了如下数学活动。

在课一开始，笔者出示了五个不同的长方形，然后提出这样的问题：在这五个长方形中，你觉得哪些长方形看起来更美观、更舒服呢？你是怎么想的呀？学生虽然研究过长方形，但对于这样的问题他们并没有思考过，他们对于长方形美的标准可能是不同的，但无论觉得哪个长方形更美观，在对问题的研讨中，必然会聚焦到长方形长与宽的关系上，这样就进入了同类量比的学习。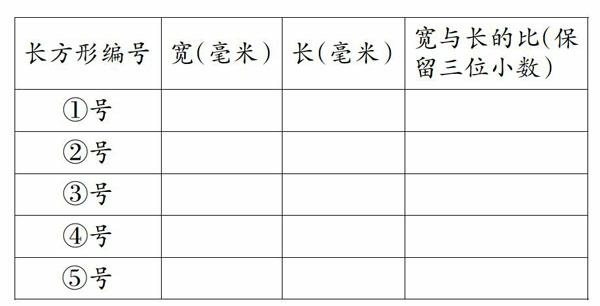

测量每个长方形的长和宽，把下表填完整。

通过对上面一系列小问题的研讨，使学生进一步体会比，知道比各部分的名称、会求比值。在明确了这些之后，教师引发学生思考“我们写出了长方形长与宽的比，也会求比值了，能回答这些长方形美的原因了吗？”因为学生在这时确实还没有找到长方形美的原因是什么，此时教师进一步点拨，请学生把比值保留三位小数，学生豁然开朗，发现2号长方形和3号长方形宽与长的比值都非常接近0.618，教师及时揭示出这就是黄金数。在这一活动中，他们会惊奇地发现自己像费希纳一样经历了一个发现黄金数的过程，从而真正使学生在数学文化的体验中挖掘数学知识的本质。

活动二：调制油漆，他们调出的绿色会一样吗？

笔者设计了调制油漆的活动，既体现了知识的应用价值，又能体现数学和美术学科的整合。用蓝漆和黄漆可以调配出绿漆，但在调配的过程中，如果蓝漆和黄漆使用的数量不同，调配出绿色的深浅就不同。有三个同学是这样调配的：小明用6桶蓝漆和4桶黄漆；小林用5桶蓝漆和4桶黄漆；小红用3桶蓝漆和2桶黄漆。猜猜看，他们调配出来的绿色会一样的吗？

猜猜看，他们调出的绿色会一样吗？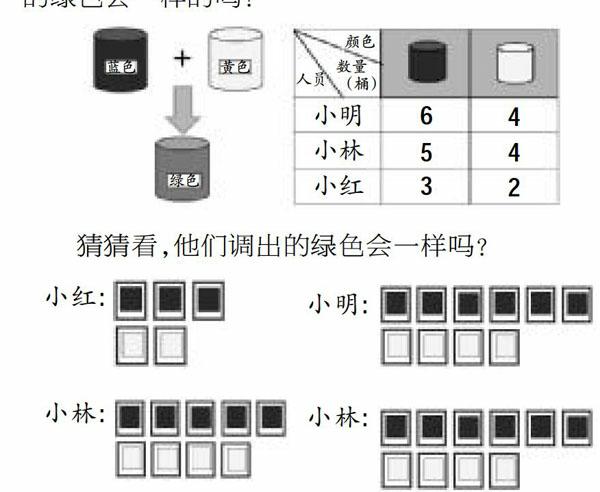

学生能够根据已知信息中蓝漆数量和黄漆数量，以份为标准，找到小明和小红的绿色是一样的，假设小林增加1桶蓝漆和4桶黄漆调配，三个人的绿色才是一样的，所以小林调配的绿色比他们俩的深一些。

活动三：带领学生发现生活中的黄金比

学生在发现黄金数的基础上，笔者继续带领学生在建筑物、艺术作品、动物的身体中找一找它们“哪两部分的比值接近0.618？”再次依托数学文化的素材加深对比的意义的理解。

实际上这些照片经常在眼前掠过，但从来没有从黄金比的角度感受到它的美。除此之外，芭蕾舞演员为什么总是踮起脚跳舞，爱美的女孩为什么总是穿高跟鞋，其实都是寻找人体的0.618。激发学生从这个视角观察世界的兴趣。

对于“负数的认识”一课的教学，教师会从学生熟悉的电梯、温度计等入手，进而联系转学中转进与转出、银行卡中输入与支出、海平面以上与海平面以下、顺风与逆风等的关系，体会负数表示意义相反的量。学习了自然数、小数、分数，为什么还要学习负数呢？原因在于，像足球比赛中进球、丢球，做生意的亏盈，水的温度零度以下该如何表示呢？负数的学习来源于需求，为了表示生活中的这些现象。从生活中寻找原型，能有效地帮助学生建构数学概念，体现数学的应用价值。

在学生学习了“角的度量”后，让他们从生活中寻找角，感受角的度量在生活中的广泛应用：儿童喜欢玩的滑梯，有的坡缓，有的坡陡，其实就是滑梯与地面的夹角不同。滑梯与地面的夹角不同下滑的速度也不同；滑梯设计成47°～49°，更适合大一点的孩子来玩，滑梯设计成38°～45°更适合幼儿和年龄比较小的孩子玩；军人站立时两脚分开呈60°是最标准的；三角钢琴中，琴盖上支起的木板与琴盖之间的夹角大约是45°，既好看美观，钢琴的音色也是最佳的；放风筝的时候也涉及角度，什么角度风筝飞得高？衣领也有角，椅子靠背也有角度，生活中随处可见角的知识，体现了学习角的度量的价值。

在数学教学中，教师要善于引导学生用数学的眼光观察现实世界，学会从周围事物中寻找与数学有关的因素，提出用数学解决的问题。这样，学生才能逐步体会到数学应用的广泛性和学习数学的价值，从而增强学好数学的信心。

二、感悟模型思想，解决实际问题，用数学的知识解释生活中的现象

在概念教学中把握本质，是数学课堂教学的灵魂。“授之以渔”比“授之以鱼”更重要，学生进行学习，重要的是学会应用，能用学到的知识去解释生活中的现象，解决生活中的问题。

生活中充满了数学信息，任何知识在生活中都是有价值的。关键要看我们是否具有一双数学的眼睛，能否捕捉到有价值的数学信息。在数学教学中培养学生的应用意识，教师要能创设情境，收集数学应用的实例，让学生用所学知识解释生活中的现象，解决新情境下的问题，在应用中加深对数学的理解和体会。

在学完长方形、正方形周长和面积之间的关系之后，教师给学生讲了一个故事：

阿凡提给大财主巴依老爷家放羊，巴依老爷非常吝啬，经常拖欠阿凡提的工钱，还在工料方面为难阿凡提。这天，阿凡提赶着羊回到财主家，巴依老爷要他把羊赶到长10米、宽2米的长方形羊圈内。可是羊群的占地面积需要36平方米，这个长方形的羊圈根本容纳不了这么多羊。吝啬的巴依老爷说：“我不管，如果你要改造，就得自己花钱去买材料做围栏。”你知道阿凡提是怎么做的吗？（动手画一画，做一做）

生：一个长方形羊圈的长是10米，宽是2米，面积是20平方米，可羊群需要的占地面积是36平方米，那么这个长方形的长可能是18米，宽可能是2米。因此，需要再买16米的材料才能装得下羊群。

生：羊圈的占地面积是36平方米，那么这个长方形的长可能是9米，宽是4米。因此，需要再买2米的材料才能装得下羊群。

师：想得好！自己买的材料越来越少了，能不能不买材料，也能解决问题呢？

生：不买材料就是利用现有的这些材料，怎么样让羊群自由自在地生活呢？

学生一边画图，一边记录：

生：周长不变，可以围不同的长方形，当长和宽相等时，这个正方形羊圈的占地面积是36平方米，它的边长是6米。这样就不用买材料了，正好能把羊群全部放进去。

生：哦，这就是前一段时间学过的规律，在周长一定的情况下，围成的正方形面积比围成的长方形面积大。

师：是呀，说得有道理。这就是学习的价值，能帮助我们解决实际问题。阿凡提正是用自己的智慧化解了巴依老爷的刁难。

正当教师要鸣锣收兵进行下一个环节时，又有学生开始提问题了：

生：除了围成正方形，还应该有其他的方法，也能让羊群自由自在的生活，我们可以借一面墙。

忽然间，大家觉得仿佛打开了一扇窗，眼睛一亮，纷纷举起了小手。

师：你是怎样想到这个办法的？

生：我在爷爷家见过借用一面墙围成的小菜园。

师：看来生活经验和活动经验对我们想问题、解决问题都会有新视角的补充，我们要有一双会发现的眼睛观察生活，让我们的思维更灵活。

生：我们还可以借助两面墙……

用一个学生喜闻乐见的小故事作为情境，把数学和阅读进行了整合，让学生在新情境中解决问题，进一步深入理解周长和面积的关系，体会数学学习的价值。这道题目属于“探索规律”的内容。探索规律是一个发现关系、发展思维的过程，有利于学生夯实基础，培养创新意识。

在学习“鸡兔同笼”时，学生理解了画图、列表、计算、列方程等方法都利用的是假设思想。学完了“鸡兔同笼”的问题，可以解决三轮车和自行车在一起的问题，可以解决蜘蛛和蝉在一起的问题，还可以解决一群人去公园划船，坐大船、小船各需要几条的问题，当然还可以解决乒乓球比赛中单打和双打的问题。

我们去商场买东西，一下子就能找到我们需要的物品在第几层，看着一排排整齐的货架，这不就是分类的价值吗？在旅游景区随处可见的汽车车牌号鲁A、贵C、冀B……是数字编码在生活中的具体应用，为什么身份证号码是18位，车牌号用文字+字母+数字的呈现方式呢？其蕴含的信息代表了汽车主人所在的省、市、地区，这也是分类思想的具体体现，有序性、唯一性、简洁性渗透其中。二维码、书刊号、门牌号等都是数字编码在不同行业、不同领域应用的价值所在。让学生在应用中学习，用所学的数学知识，解释生活中的现象，提升了学生的应用意识和实践能力，促进了知识的迁移和融会贯通。

三、设计实践活动，沟通联系，在体验中促进数学思考

“综合与实践”是以问题为载体、以学生自主参与为主的学习活动。它有别于学习具体知识的探索活动，更有别于教师的直接讲授，教师通过问题引领，让学生全程参与实践过程，经历相对完整的学习活动。它的核心是学生在教师的引导和帮助下有目标地、自主地参与实践活动。

在四年级学习了“大数的认识”，学生知道了10个一千万是1亿。1亿到底有多大呢？

可以结合情境，提出如下问题：1亿张纸摞起来有多高？1亿秒大约多长时间？1亿根头发到底有多少？……

教师让学生先猜一猜：有的学生说1亿张摞起来有六层楼那么高；1亿秒大约有一年吧；1亿根头发得有10万人的吧。这是你们的猜想，到底1亿有多大，然后让学生结合身边的、熟悉的事物进行体验、推算和验证等。

学生通过一本数学书大约100页，也就是50张纸，2本书就是100张纸，摞起来大约有1厘米，1000张纸摞起来大约是10厘米，1万张纸摞起来大约是1米高。学生可以通过累加，利用部分推知整体的方法，根据相邻计数单位之间的进率都是10来推算，列表如下：

10万张纸摞起来有教学楼三层楼那么高，1亿张纸摞起来大约是1万米，比珠穆朗玛峰（8844.43米）还高。

500张1包的A4纸放在秤上称一称大约是500克，1000张纸大约是1000克，也就是1张纸大约是1克。1亿个1克合起来是100吨，相当于10头非洲象那么重。

让学生在练习本上点点，1秒钟点一个点，点1分钟60个点，照这样计算，不吃饭、不睡觉，其他的事都不做，只做点点这件事，点1亿个点需要3年2个多月。也就是从上小学一年级的第一天起到现在四年级第一学期学习大数的认识，还差一些没点完呢。

成年的黄种人的头发大约有10万根，1000个成年人的头发根数合在一起大约是1亿根。这就是在让学生体会，1000个10万是1亿。

结合生活情境，体会1亿到底有多大。从长度、质量、时间等多个维度，给学生以清晰的认识，1亿到底有多大，可以触摸、可以感觉、可以想象，最后学生及时反思，1亿张纸摞起来原来那么高；一个人的头顶有那么多根头发，难以想象……结合生活经验，让学生澄清了认识偏差，在活动中加深了对十进制计数法的理解，既沟通了数学知识间的联系，也沟通了数学和生活的联系，运用数学的思维方式进行思考，帮助学生积累数学活动经验，培养了学生的数感，提升了学生的核心素养。

除了数学学科内部的实践活动，与其他学科整合成为一种合理与必然。如学习“曹冲称象”一课，可以思考，这件事体现的数学思想方法是什么？问题解决的策略是什么？古今中外的聪明人都有谁，他们的智慧是如何体现的？他们是怎么想到的，我怎么没想到……这样就把所有学科的学习都统一到一起，以培养学生的理性思维，提高应用意识，从而解决新情境下没有模式的问题。

学科整合并非淡化学科，学科自身的独特性不等于僵化学科的边界，而是在各司其职的基础上相互融通，也就是软化学科边界，其价值在于为类似“科学、技术、工程和数学”等新兴学科的创生提供了空间，学科整合已是必然趋势。

综上所述，在小学数学教学中要培养学生的应用意识，教师就要善于在“数学”与“生活”之间架起一座桥，让学生有机会亲身实践，用自己所学知识解释生活中的现象，既能借助生活经验理解数学，又善于用数学的眼光观察生活，使他们真正感受和体验到数学的魅力与价值，增进对数学的理解和应用数学的信心；能从生活中提出数学问题，能运用数学的知识方法解决现实世界中的问题。让学生在“实践—创新—再实践”的过程中，提高学生的应用意识和实践能力。

参考文献：

[1] 吴正宪，等.和吴正宪老师一起读数学新课标[M].北京：教育科学出版社，2013.10.

（北京市顺义区教育研究考试中心 101300）