以学为中心的单元教学活动设计初探

张丽珊

【摘要】“双减”政策下，如何在有限的时间内达到高效的教学，对教师而言是新的挑战.要实现这一目标，以学为中心的单元教学是有效的途径之一.笔者以“一元二次方程”为例，以学为中心尝试探究新知建构类单元教学活动.

【关键词】以学为中心；初中数学；单元教学

以学为中心起源于建构主义理论，是在以学生的发展和主动学习过程中，在教师的帮助下，学生完成新知识和能力的建构［1］.《义务教育数学课程标准（2022年版）》指出：“数学知识的教学，要注重知识的‘生长点’与‘延伸点’，把每堂课教学的知识置于整体知识的体系中，注重知识的结构和体系，处理好局部知识与整体知识的关系，引导学生感受数学的整体性，体会从不同的角度加以分析、从不同的层次进行理解”［2］.单元教学恰好能实现课标精神，使学生感悟知识体系，从整体角度更好地理解知识点之间的关联.笔者以“人教版第21章一元二次方程第一课时”教学设计为例，尝试探究新知建构类单元教学活动，促进学生的深度学习.

1 以学为中心的单元教学设计思路

课程内容要素→課程目标的设定→课程教学资源→课程教学过程→课程教学反馈→反思感悟.

以学为中心，逐步推进.

2 构建方程的单元教学

2.1 基于单元教学的文本建构

人教版第21章“一元二次方程”属于“方程与函数”领域，学生已学习了“一元一次方程”与“二元一次方程（组）”，在此基础上进行研究学习一元二次方程，以类比、创设情境方法探究一元二次方程的概念及一元二次方程的根（解）的含义.本节课重点是理解一元二次方程概念及其有关概念，难点在于把实际问题转化成数学模型.用单元教学理念让学生初步体会从整体角度看待整章单元的知识，以学为中心建构体系，渗透研究方程的通用方法，促进学生的深度学习，培养学生的高阶思维能力.

2.2 基于单元教学的目标建构

（1）知识技能：①理解一元二次方程的概念，会把一元二次方程化成一般形式；②理解一元二次方程的根（解）的含义.

（2）数学思想：由特殊到一般、分类思想、类比归纳思想、转化思想等.

（3）核心素养：模型思想、应用意识.

2.3 基于单元教学理念的活动设计

活动一 回顾旧知，创设情境引入（预习任务清单）

1-1 回忆一元一次方程、二元一次方程（组）及方程（组）的解等相关知识.

1-2 对比下列方程说出它们的区别和联系：

（1）x－2=0;（2）x=4;（3）x=0;

（4）x=－4;（5）x+2x－24=0．

1-3 要组织一次排球邀请赛，参赛的每两支队之间都要比赛一场（单循环赛），

（1）若有3支球队参赛，则全部比赛的场数是____；若有4支球队参赛，则全部比赛的场数是____；有x2－4x－5支球队参加邀请赛，则全部比赛的场数是____；（2）根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，比赛组织者应邀请多少支队参赛？若设应邀请个x支队参赛，则可列方程____．［3］

思考 （1）上述所列的方程的左右两边是怎样的代数式？（2）所列的方程含几个未知数？（3）请把所列方程按下列要求化简：①等式的右边为零；②等式的左边的整式按未知数字母降幂排列.

引导学生认真思考，与所学方程知识类比，如何定义这个方程？方程的解是什么？如何求解？

设计理念分析 1-1是为引入一元二次方程做准备，帮助学生回忆方程的定义及解法；1-2通过与一元一次方程比较，渗透分类思想及为一元二次方程求解（本质是降次）做铺垫，蕴含对根的判别式的分类；1-3结合教材内容，从特殊到一般，找出规律列出方程，进而求解，培养学生从实际问题抽象出方程模型意识的能力；归纳总结一元二次方程的一般形式及其有关的概念.通过设计活动一的几个问题，构建了本节课的主要学习内容，有利于知识的整体架构及学习方法的探究.通过预习任务清单让学生养成主动学习、以数学的眼光观察思考社会问题.

活动二 探究新知，建构体系

2-1 将下列方程化为一元二次方程的一般形式，并写出其中的二次项系数、一次项系数、常数项：

（1）3xx－1=5x+2；

（2）4x=49；

（3）x（x－1）=56.

小结：怎样把一元二次方程化为一般形式？说出解题步骤！

2-2 判断x=－7和8是否为方程x2－x=56的根.

2-3 根据下列问题列方程，列出关于x的方程，并将其化成一元二次方程的一般形式：

（1）正方形的面积是25，求正方形的边长x；

（2）参加一次聚会的每两人都握一次手，所有人共握10次，有多少人参加聚会？

2-4 解方程：

（1）y=25； （2）（x+1）=25；

（3）x+2x+1=25； （4）xx+2=24.

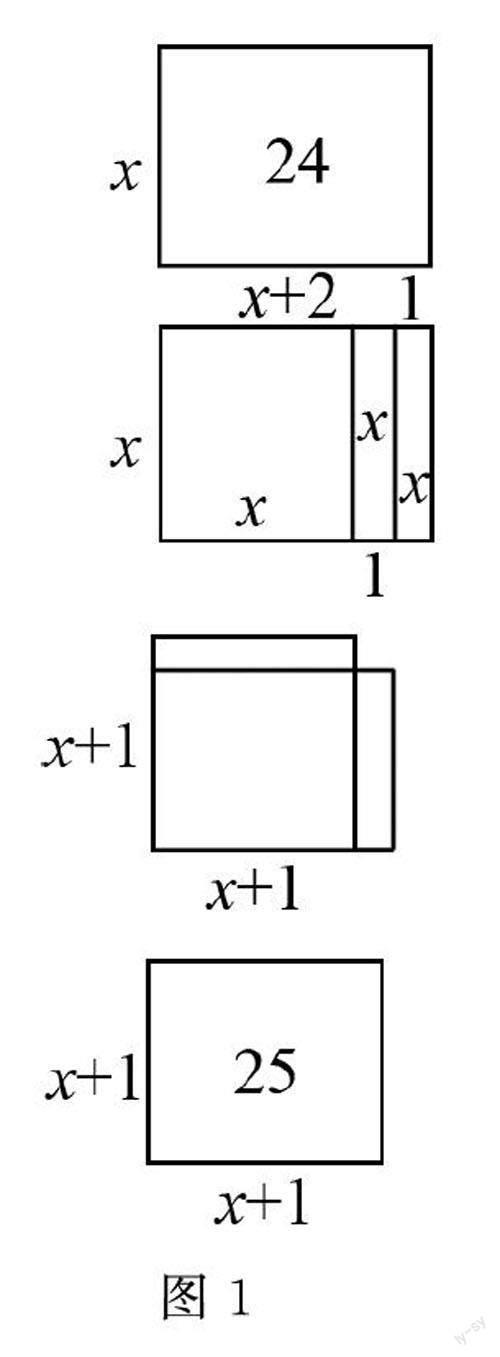
你能用几何图形如矩形的面积来表示（4）的解法吗？

师生活动 学生先独立思考，再与小组成员交流，最后教师巡视，根据学生反馈情况给予适当点拨，建构本章的知识体系.

设计理念分析 2-1帮助学生对一元二次方程一般形式的理解，其中（2）和（3）是为了后续求方程的根做准备；2-2承接2-1中的（3），理解一元二次方程的根可能不止一个，也是活动一中的部分解答，再根据实际意义做出判断；2-3结合实际问题展开，培养学生模型意识，其中的（1）是为了后续用几何图示表示解法提供参考，（2）类比活动一中单循环比赛问题，加深对实际问题的理解，感悟类比思想，转化思想；2-4中4个小题既可以用直接开平方法也可以用因式分解法，解上述方程的本质是降次为两个一元一次方程，而（4）由（3）类比迁移用配方法及借鉴苏科版“数学实验室”板块中介绍配方的几何表示，如图1所示，帮助学生以拼图视角看配方法［4］.并介绍相关的数学史.数形结合，理解解法的几何意义，体会从不同的角度思考解法之间的内在联系，为后续进一步学习打下基础，感悟从整体的角度学习研究数学知识，发展学生的高阶思维能力，进而培养学生深度学习.

通过活动二，学生经历了知识点→解法→数学思想，进一步建构体系，将知识点关联，完成了一元二次方程与一元一次方程的体系建构，达到知识的“生长点”.

活动三 总结提升

归纳总结，以知识结构图促进学生对整节课教学脉络的理解，体会研究方程的一般思路：建立方程模型解决实际生活中遇到的问题，求解的基本思想是“降次”，感悟数学思想.

活动四 拓展延伸

4-1 关于c的一元二次方程x2－c=0一定有解吗？说明理由．

4-2 参加一次聚会的每两人都握一次手，张强同学说：“所有人共握手16次”，张强同学的统计是否正确？说明理由．

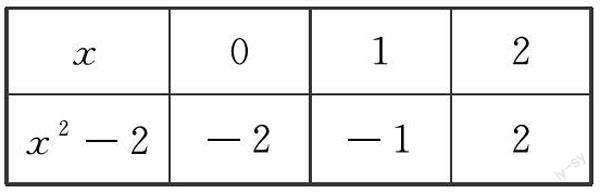
4-3 阅读材料：一般来说，如果一个数代入方程左边得到的值为负，把另一个数代入得到的值为正，则在这两个数之间有可能有方程的解.例：

由表可知方程x2－2=0的解在1与2之间．根据这个原理估计方程x2－2x－13=0的解（精确到个位），并判断是否有一个根大于4.5？

师生活动 让学生有充分的时间考虑，邀请学有余力的孩子分享不同的解法，如：方法一：当x=4时，x－2x－13=－5；当x=5时x－2x－13=2 ；方法二：当x=4时，x－2x=8＜13；当x=5时，x－2x=15＞13.以此类推，方程x－2x－13=0的解在4与5之间或者－3与－2之间．

设计理念分析 4-1与1-2相呼应，对c进行分类，感悟特殊到一般的思想；4-2与1-3单循环赛问题相似，体会建模思想列方程，求解过程中可通过代入数值盘点方程的解为4-3提供参考；4-3此题改编自2011年版《数学课程标准》例52，用二分法估计方程的解，初步感悟通过代入数值计算也是求方程解的有效途径.在教学中渗透函数思想，为后续学习二次函数铺垫，感悟蕴含不同角度的解题思想，积累活动经验.循序渐进，用联系的、整体的观点组织教学内容，即单元教学，最终实现深度学习.

通过活动三和四，进一步建构体系：从学法（猜想、验证、小结、反思、迁移、应用等）→素养（建模、创新、辩证等综合能力）；整合单元知识，完成对知识点→解法→数学思想→学法→素养的体系建构，有利于培养学生发现问题、研究问题的方法、批判辩证思维及创新意识，有利于发展学生的高阶思维及构建能力.

活动五 课后作业，有效反馈

5-1 根据下列问题，列出关于x的方程，并将其化成一元二次方程的一般形式：

（1）把长为1的木条分成两段，使较短一段的长与全长的积等于较长一段的长的平方，求较短一段的长x；

（2）圆的面积为2πm2，求圆的半径x．

5-2 按要求写出相应的一元二次方程：二次项系数、一次项系数、常数项分别为2，－1和3．

5-3 下列哪些数是方程n的根？

－4，－3，－2，－1，0，1，2，3，4.

5-4 对于一元二次方程，我国及其他一些国家的古代数学家曾研究过其几何解法，以方程x2+2x-35＝0为例，公元9世纪，阿拉伯数学家阿尔·花拉子米采用的方法是：将原方程变形为（x+1）2＝35+1，然后构造图形求解，一方面，正方形的面积为（x+1）2；另一方面，它又等于35+1，因此可得方程的一个根x＝5，请根据阿尔·花拉子米的思路，画出解方程x2-4x-21＝0时构造的图形.

5-5 解方程：

（1）4x=25； （2）（x+2）=49；

（3）x+2x+1=9.

設计理念分析：适当的作业有利于巩固对所学知识的理解，有效反馈便于教师辅导有需要帮助的学生，5-1至5-3属于基础知识，提高学习自信心，可以网络答题直接反馈，反馈方式多样化，结合线上线下提升反馈的有效性及趣味性；5-4属于数学史的延伸，为发展学生研究素养，自我反思，进而促进学生深度学习与建构体系的能力.

3 构建“以学为中心”单元教学设计的感悟

3.1 有利于章节的整体把握及框架的建构

（1）由于学生的局限性，若只侧重单一知识点的教学，那么学生多数仅能模仿且形成低阶思维；而通过以学为中心的大单元教学，学生获得了章节知识的研究方法，以整体视角来审视章节中的知识点，有利于培养学生的研究素养及整体把握，通过对数学史的介绍，鼓励学生养成阅读的习惯，查阅相关学习资源，实现从不同方式获取学习资源，形成主动学习的习惯，对于数学原理的来龙去脉更有感悟，利于将来向有序深入学习.（2）有利于知识框架的建构，比如函数领域，学习反比例函数时，类比一次函数的研究方法（如作图时k，b对图象的影响），研究学习k对反比例函数图象与性质的影响，进而归纳出函数中不同参数对图象及性质的影响，进而应用数形结合思想解决实际问题，使学生在将来学习其他函数时形成研究框架与思路，促成高阶思维、深度学习的能力.

3.2 有利于达到知识的贯通

新知建构类单元教学需要对教材进行整合、理解，关注知识的自然生成及蕴含思想，找寻其内在关联.从不同的维度、整体的观点构建知识体系，从不同层面、多渠道引导学生思考，让学生在解决问题的过程中形成独立意识与创新意识，如在拼图解释配方法及介绍数学史中，课堂教学活动的处理可以更加大胆与开放，让学生的思维碰撞出火花，感受数学的神奇魅力［5］.

3.3 以学为中心的教学应注意的问题

教师自身需随着时代的发展更新教育理念、提升自己的个人专业素养；教学设计需加强对学情的了解，目标有不同的层次，多鼓励学生参与意识；教学方式多样化，选择有利于学生发展及目标达成的方式；反馈评价多维化，注重对学习过程的评价，淡化对分数的过度关注，促进学生探索适合自己的学习方法.

【基金项目：此文作为核心成员参与周卓主持的厦门市湖里区2021年度区级课题《“以学为中心”的初中数学活动课程的教学策略研究》（课题批准号：2021029）的研究成果】

参考文献：

[1]陈正.以学为中心的课堂教学实施与思考[J]．黑龙江教育（理论与实践），2022（4）：46-48.

[2]王建波.义务教育数学课程标准[M]．北京；北京师范大学出版社，2012.

[3]林群.人教版九年级数学教师教学用书[M]．北京；人民教育出版社，2014.

[4]汪晓勤，栗小妮，数学史与初中数学教学——理论、实践与案例[M]．上海；华东师范大学出版社，2019.

[5]陈小霞.立足七个维度构建高效课堂[J]．中学数学教学参考（中旬），2021（4）：39-40.