由一道错题谈参变分离方法的运用和启示
2023-06-03广东省汕尾市陆河县河田中学516700李国振李岸模
广东省汕尾市陆河县河田中学(516700) 李国振 李岸模
一、引言
一节课上恰好讲到一道函数导数题目,课堂上讲完它的一般解法后,突发奇想这道题能不能用参变分离方法解决?然后带着学生用参变分离的方法按部就班的往下推进,到了最后也顺利解决了问题. 这时,一个学生指向图像的左半部分问:“老师,左边是不是也有符合条件的解? ”顺着他的思路,题目果然出错. 然后就是各个书籍和网上去查这道题,发现所有地方这道题解答都是一样,出现了问题.
二、题目与参考答案
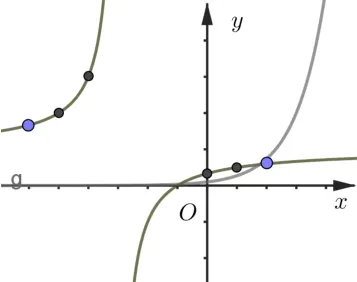
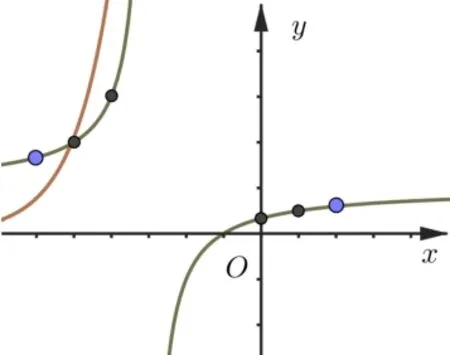
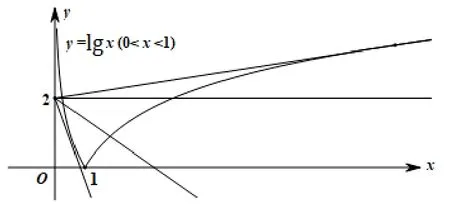
题目已知不等式(kx+3k)ex 参考答案原不等式(kx+3k)ex 当x<0 时,f′(x)>0,所以在(−∞,0)上单调递增;当x>0时,f′(x) < 0, 所以在(0,+∞)上单调递减. 又f(−1) = 0, 且x> 0 时,f(x) > 0,因此g(x) =k(x+3)与的图象如图1, 当k≤0 时, 显然不满足条件, 当k> 0 时,只需要满足即,解得,故答案选D. 图1 x(−∞,x1)x1(x1,−3)(−3,x2)x2(x2,+∞)f′(x)−0++0−f(x)↘极小值↗↗极大值↘ 图2 题目的参考答案显然是忽略了g(x) =k(x+3) 与在第三象限相交时也有两个符合条件的解. 实际上,在左半部分异常陡峭的图像上, 如果没有彻底的参变分离,而通过肉眼发现符合条件的解确实有一定的难度. 图3 参考答案的方法其实非常好, 它把已知条件通过化简,化归为两个简单常见的函数, 这两个函数比较容易作图,这是该方法的一个优点. 但是在求解的过程中, 因为落在x= −3 左边图像过于陡峭, 未在图中得以呈现, 导致对应的解被遗漏,而后题目设计的时候也就出错了. 而我们如果顺着标准答案的求解过程,也觉得这个过程非常完美. 而当实现完全的参变分离,当整个函数的图像完全画出来,因为y=k太容易与之对比求解了,所以在求解的时候更不容易出错. 但是完整的参变分离往往其中一个函数图像会非常难画,这是彻底的参变分离的缺点. 原不等式(kx+3k)ex ①当x= −3 时,不等式等价于0 < −2e3,显然不符合条件. ②当x> −3 时, 不等式等价于,设f(x) =(如图4),即kex 图4 ③当x< −3 时, 不等式等价于,即kex>f(x). 对于y=kex,是经过定点(0,k)的单调函数. 当k< 0时,y=kex是单调递减函数,整个图像落在x轴下方,此时,有无数个整数点符合条件, 这与有且只有两个整数解矛盾,不符合条件. 当k> 0 时,y=kex是单调递增函数,整个图像落在x轴上方,此时,有两种可能. 图5 图6 根据2021 年北京高考数学卷第15 题,我们编制了对数函数与一次函数相结合的考题: 训练题已知函数f(x)=|lgx|−kx−2,给出下列四个结论: ①若k=0,f(x)恰有2 个零点; ②存在负数k,使得f(x)恰有个1 零点; ③存在负数k,使得f(x)恰有个3 零点; ④存在正数k,使得f(x)恰有个3 零点.其中所有正确结论的序号是____. 解答对于f(x)的零点, 我们把它分离成y=kx+ 2 和y= |lgx|两个函数, 转变成两个函数的图像交点问题,y= |lgx|如图7. (1)y=kx+2 经过定点(0,2), 当k= 0 时, 直线与y=|lgx|显然有两个零点,所以①正确. (2)当k< 0 时,由图7 可知,有三种可能,在0 (3)当k>0 时,如下图,也有三种可能,在x>1 处相切时一个零点,在相切与平行x轴之间有三个零点,其余零个零点,以下求相切时的斜率. 同上可得直线y=kx+ 2 与曲线y= lgx(x>1) 相切于点P(t,lgt), 由函数y= lgx得, 由题意可得解得, 所以, 当时,函数f(x)有三个零点,故④正确. 故答案为: ①②④. 评注原函数十分的复杂,难以处理,利用分段函数处理也非常麻烦,但是利用参变分离后的两个函数相对来说简单很多,y= |lgx|是一个很常见的函数,y=kx+2 是过定点(0,2)的直线,我们可以直观的从图像中观察出直线斜率对于交点的影响,进而利用导数解决切线问题. 这种化复杂为简单,化不常见为熟悉的化归思想,在解决这类问题时十分的有用. 《普通高中数学课程标准》指出,逻辑推理能力的主要表现为:“掌握推理基本形式和规则,发现问题和提出问题,探索和表述论证过程,理解命题体系,有逻辑地表达和交流.”[1]参变分离方法,能培养学生逻辑推理的能力,是化归思想的体现. 通过观察、理解问题,对问题进行有条理、合乎逻辑的变形,进而从复杂的思路中找到解决问题的方向. 面对一个含参变量的函数,我们使用参变分离方法,能把复杂的函数变成两个相对简单的函数. 以上所采用的三种不同的分离方法,大同小异. 至于说哪一种简单,需要视解题者对每种不同函数的熟悉程度而定. 参变分离的方法能降低运算量,但其教学难点是把一个函数图像的问题转变成两个函数图像的问题. 在教学中,需要在比较图像这个地方对学生进行强化突破. 任何一种方法, 如果没有把问题简单化都不是好方法,参变分离方法也一样. 我们的着力点是简化函数,简化运算.同时,参变分离方法也是数形结合的一种体现,把零点问题,不等式恒成立问题转化为两个函数的关系问题. 在处理这一类问题的时候,唯有数与形的完美结合,我们才能找到最简单的方向,快速有效地解决它. 正因为参变分离方法的实用性和有效性,在平时的教学中,我们应当让学生能够熟练掌握这一方法.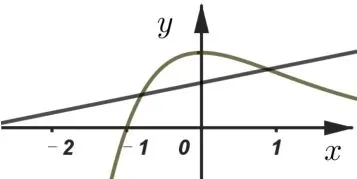
三、彻底的参变分离解决方案



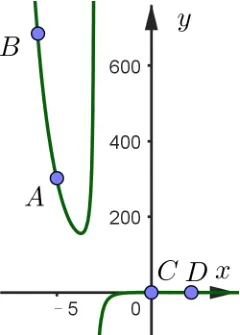
四、错误成因及方法优缺点分析

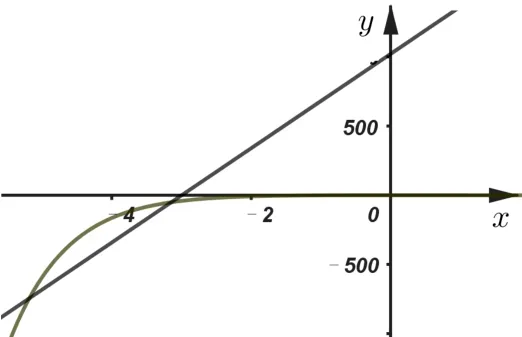
五、另外一种不完全的参变分离方法
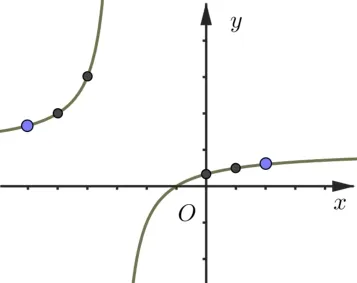


六、学以致用——编制基于参变分离方法的训练题
七、教学启示
(一)体现化归思想,培养逻辑推理能力
(二)重视方法本质,突破教学难点
(三)重视方法的使用,培养数形结合能力
