一次有趣的探究之旅

史子集

一天，我遇到一道看似平淡无奇，但是探究起来非常有趣的题目：

已知线段AB的长为10cm，点A、B到直线l的距离分别为6cm和4cm，则符合条件的l的条数为（ ）。

A.1 B.2 C.3 D.4

解答这类题目，画出图形是关键。

我从A、B两点与直线l的位置关系入手进行分类讨论。

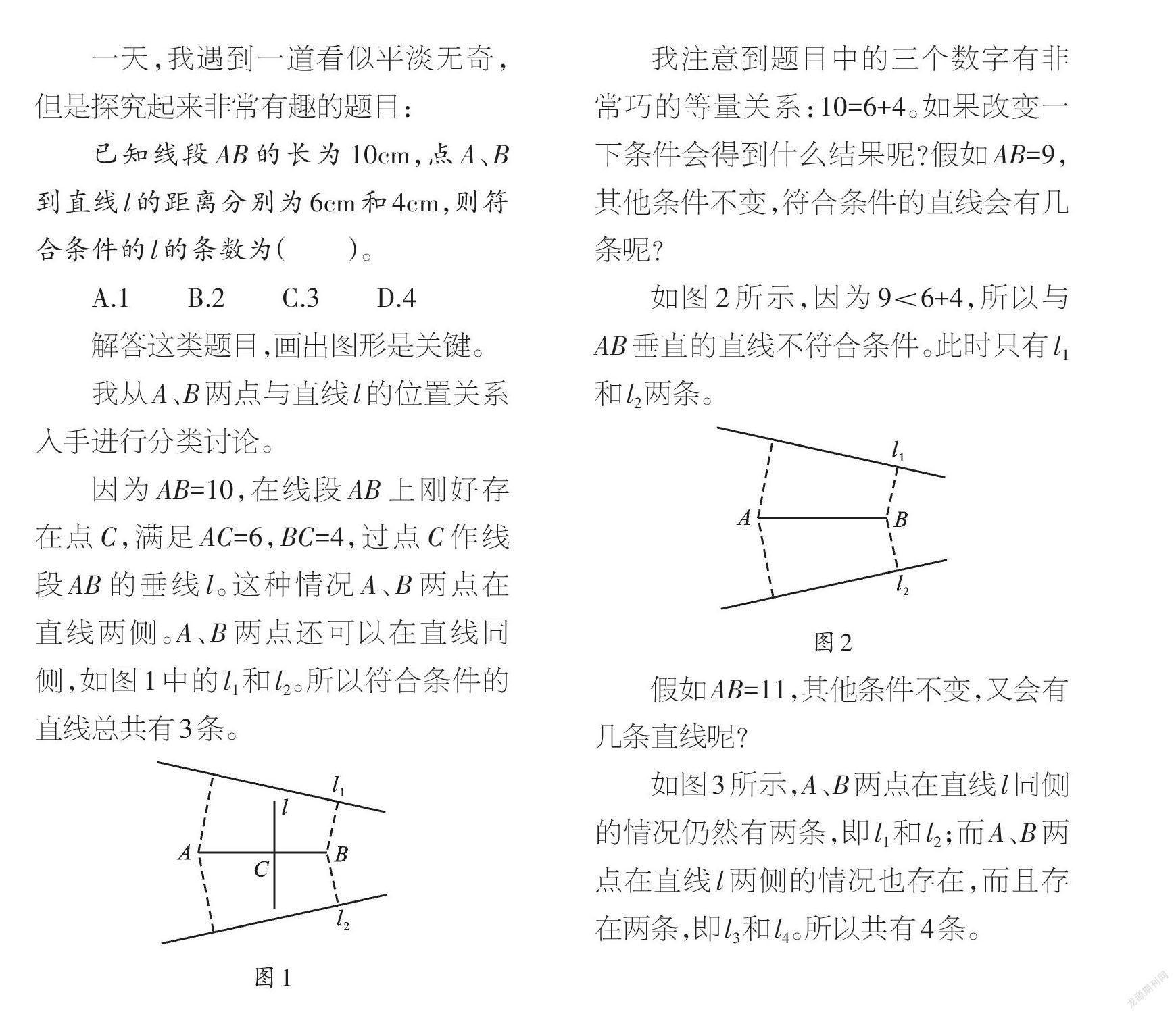
因为AB=10，在线段AB上刚好存在点C，满足AC=6，BC=4，过点C作线段AB的垂线l。这种情况A、B两点在直线两侧。A、B两点还可以在直线同侧，如图1中的l1和l2。所以符合条件的直线总共有3条。

我注意到题目中的三个数字有非常巧的等量关系：10=6+4。如果改变一下条件会得到什么结果呢？假如AB=9，其他条件不变，符合条件的直线会有几条呢？

如图2所示，因为9<6+4，所以与AB垂直的直线不符合条件。此时只有l1和l2两条。

假如AB=11，其他条件不变，又会有几条直线呢？

如图3所示，A、B两点在直线l同侧的情况仍然有两条，即l1和l2;而A、B两点在直线l两侧的情况也存在，而且存在两条，即l3和l4。所以共有4条。

综合以上情况，我得出结论：已知AB=d，A、B两点到直线l的距离分别为m和n，则

（1）当d=m+n时，符合条件的直线存在3条;

（2）当d

（3）当d>m+n时，符合条件的直线存在4条。

我兴高采烈地把这个结论拿给老师看，老师微微一笑说：“AB=2时呢？”

经过分析，原来符合条件的直线只有1条了，如图4所示。

我把以上各种情况連贯起来看，发现当A、B两点之间的距离逐渐减小时，l1和l2两条直线逐渐合并成一条，最后一条都不存在了。

我重新总结结论如下：已知AB=d，A、B两点到直线l的距离分别为m和n，假设m>n。

（1）当d>m+n时，符合条件的直线存在4条;

（2）当d=m+n时，符合条件的直线存在3条;

（3）当m-n

（4）当d=m-n时，符合条件的直线存在1条;

（5）当d

我再一次拿给老师看时，老师表扬了我的钻研精神，同时，建议我找找九年级上册的教材，自学圆的内容，学完后会对上面总结的结论有更深刻的理解。小伙伴们，我们一起继续探究吧。

教师点评

小作者对这道题目的探究之旅达到了“做一题，通一类”的效果。此次探究过程不仅培养了他分类讨论等严谨的数学思维，更锻炼了他锲而不舍的钻研精神。相信自学到“圆和圆的位置关系”时，小作者会有豁然开朗的亲切感受。

（指导教师：苏冠男）