四边形外接圆半径问题的探究

华南师范大学数学科学学院(510631) 邓清睿 韩彦昌

一、问题背景

外接圆问题是历年来较为热门的探究问题, 主要涉及:四点共圆的证明[1]、利用外接圆性质处理问题[2-3]以及寻找出或作出辅助圆求解问题[4]. 对四边形外接圆问题的探究方面,已经取得一些研究成果: 圆内接四边形的一个面积公式[5]: 已知四边形四边的长度,得到该四边形面积公式;四边形外接圆的半径公式[6]: 已知四边形四边的长度,得到其外接圆的半径公式等.

二、原题呈现与解法

题目1(2022 年“大梦杯”福建省青少年数学水平测试第7 题)如图1,ABCD为圆O的内接四边形, 且AC⊥BD, 若AB= 10,CD= 8, 则圆O的面积为____.

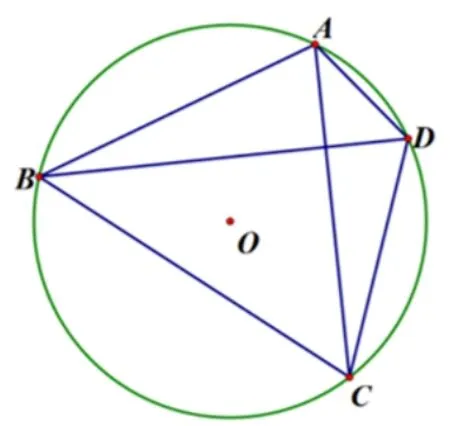
图1

构图分析对角线互相垂直,一组对边AB,CD的长度确定(可以想象线段AB的长度固定,A,B两点分别在对角线CA,BD上滑动)这样的四边形不确定,当然面积也不确定. 再附加四点共圆的条件这样的四边形唯一. 换一个角度分析: 在半径大于10 的圆上找两点A,B,使其弦长为10,过A,B引两条互相垂直的弦,会产生唯一的圆内接四边形ABCD,当CD=8,外接圆的面积唯一确定.

解法1如图2,延长AO交圆O于点F,连接BF,记AC与BD交点为E. 因AF为圆O直径,故∠ABF=90◦.由AC⊥BD,则∠AED= 90◦= ∠ABF. 由弧AB所对圆周角∠ADB= ∠AFB, 则Rt∆ABF∽Rt∆AED. 同理可得,Rt∆ABE∽Rt∆DCE,则. 由于Rt∆ABF∽Rt∆AED,则,则,则BF=8. 故.

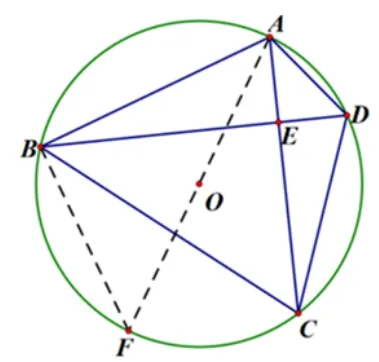
图2

解法2如图3, 延长AO交圆O于点F, 连接BF,CF, 记AC与BD交点为E. 则AB⊥BF,AC⊥CF. 由AC⊥BD,则BD//CF,BFCD为圆内接梯形,则为等腰梯形,因此BF=DC=8. 故.

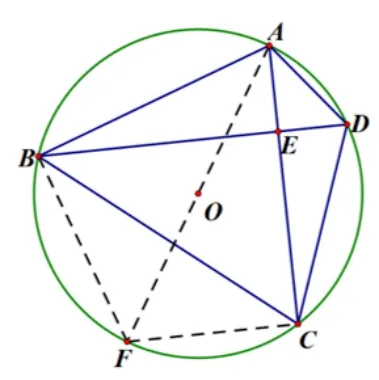
图3

三、推广结论

结论1如图4,已知AB、CD及对角线夹角∠AFB= 90◦, 则四边形ABCD的外接圆半径为.

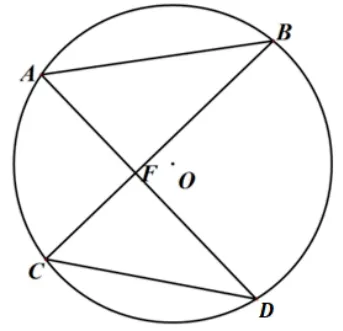
图4

结论2如图5.1 和图5.2,已知AB、CD及对角线夹角∠AFB=√α(α90◦),则四边形ABCD的外接圆半径为.

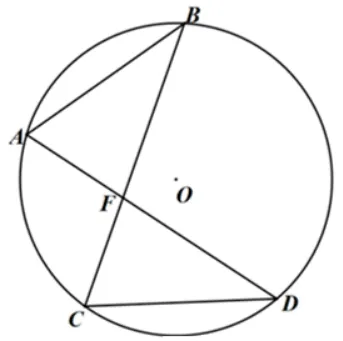
图5.1

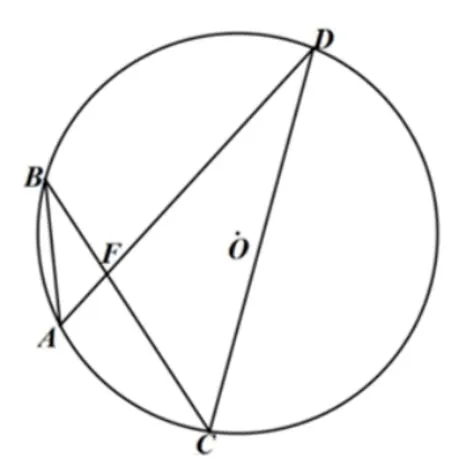
图5.2

结论3如图5.1 和图5.2,已知圆内接四边形ABCD,夹角∠AFB=α及外接圆O的半径r,则.特别地,当α=90◦时,.

注记结论1 是结论2 和3 的特例. 因此,以下我们只证明结论2 和3. 结论2 和3 说明圆内接四边形,固定对角线夹角和四边形的一条边,则该圆半径和这个圆内接四边形一边的对边长是个一一映射;进一步地,圆内接四边形,固定对角线夹角和四边形的一条边,则圆和这个圆内接四边形也是个一一映射.

四、结论证明

结论2 的证明已知AB、CD及对角线夹角∠AFB=α(α90◦),求外接圆半径r. 分两种情况进行讨论.

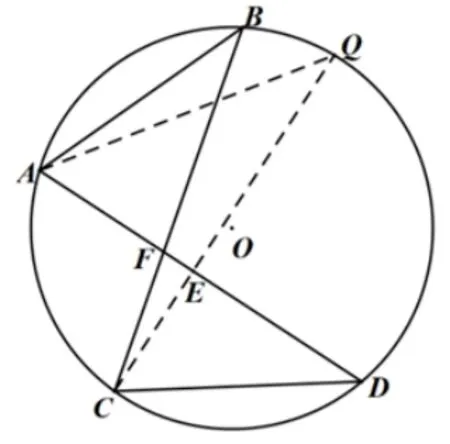
图6

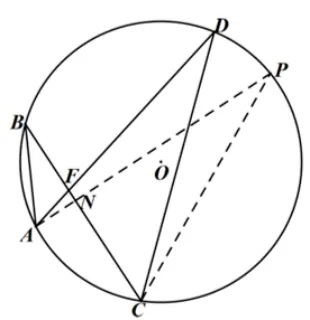
图7

五、结论应用

例1(2022 年全国高中数学联赛山东预赛第5 题)若单位圆内接四边形对角线互相垂直,则该四边形四条边平方和是____.

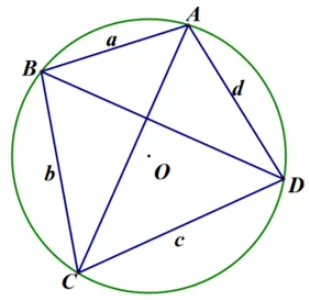
图8

例3设圆O半径r为8,圆中一内接等腰梯形一边长为10,对角线夹角为60◦,求邻边长是多少?

分析根据结论2 可知, 若梯形腰长为10, 则不满足条件, 故梯形固定(如图9), 且上底边长必为10,下底边长确定,因此问题即为求梯形的腰长.此时,将AC=BD=x代入结论3公式可得,可计算出腰长为8.

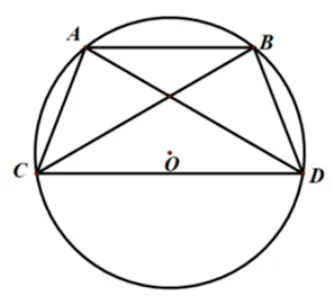
图9