一道全国高中数学联赛二试题的另一种解法

☉福建省泉州第五中学 黄种生

一道全国高中数学联赛二试题的另一种解法

☉福建省泉州第五中学 黄种生

题目（2013年全国高中数学联赛二试第4题）设n，k为大于1的整数，n＜2k.证明：存在2k个不被n整除的整数，若将它们任意分成两组，则总有一组有若干个数的和被n整除.

原题提供的解题思路如下：

若n是2的幂，设n=2r，r≥1，且r＜k，则选取的2k个数为2r-1，2r-1，2r-1，1，1，…，1.

若n不是2的幂，则选取的2k个数为-1，-1，-2，-22，…，-2k-2，1，2，22，…，2k-1.

可以证明选取的2k个数符合条件（证明略）.

本文提供另一种解法，也是构造性证明，构造的思路如下：

（1）这2k个非零整数的绝对值小于n，这样可以保证它们都不被n整除；

（2）这2k个整数中有若干个数的和等于n或-n，这样可以保证有若干个数的和被n整除；

（3）分组时，若小组内不出现和为零的数，则和等于n或-n的若干个数必须在同一小组.

证明：构造数列｛am｝（1≤m≤2k+1），使其满足以下三个条件：

（1）a1=1，a2=-1；

（2）|a1|≤|a2|≤…≤|a2k|＜n，|a2k+1|=n；

（3）m＞2时，若am＞0，则必存在1≤i1，i2，…，it＜m，使得aij＜0（j=1，2，…，t）且am=-（ai1+ai2+…+ait）；若am＜0，则必存在1≤i1，i2，…，it＜m，使得aij＞0（j=1，2，…，t）且am=-（ai1+ai2+…+ait）.

以下对k用数学归纳法证明满足上述条件的数列存在.

（1）当k=2时，n＜4，

n=2时，数列1，-1，1，1，2，符合条件；n=3时，数列1，-1，1，1，3，符合条件.命题成立.

（2）设n=k0时，命题成立，则对于n＜2k0，存在数列｛am｝（1≤m≤2k0+1）满足条件.当n=k0+1时，

①若n＜2k0，构造数列｛bm｝（1≤m≤2k0+3），使得：

显然，数列｛bm｝（1≤m≤2k0+3）符合条件.

②若2k0

≤n＜2k0+1，当n=2n0时，n0＜2k0，存在数列｛am｝（1≤m≤2k0+1）满足条件，构造数列｛bm｝（1≤m≤2k0+ 3），使得bi=a（i1≤i≤2k0+1），b2k0+2=a2k0+1，b2k0+3=-2a2k0+1.

显然，数列｛bm｝（1≤m≤2k0+3）符合条件.

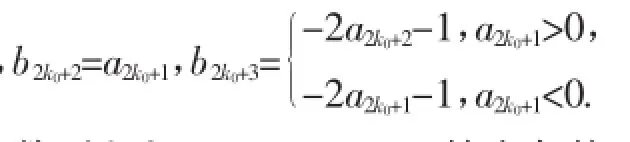
显然，数列｛bm｝（1≤m≤2k0+3）符合条件.

所以，符合条件的数列存在.

以下用反证法证明结论.对于数列｛an｝中的前2k个数a1，a2，…，a2k，由于1≤|ai|＜n，所以它们不能被n整除，假设把它们分成A，B两组，两组中均不存在若干个数的和为n的倍数.不妨设1∈A，因为1+（-1）=0，所以-1∈B，用数学归纳法可以证明，当an＞0时，必有an∈A；当an＜0时，必有an∈B，具体证明如下：

（1）当n=1，2时，a1∈A，a2∈B，结论成立.

（2）设当n≤k时，结论成立，当n=k+1时，若an＞0，由于存在1≤i1，i2，…，it≤k，aij＜0（j=1，2，…，t），使得an= -（ai1+ai2+…+ait），由假设知，aij∈B（j=1，2，…，t），所以an∈A.同理，当an＜0时，必有an∈B.综上，命题成立.

又因为|a2k+1|=n，若a2k+1=n，则B组中必有若干的数ai1，ai2，…，ait，它们的和为-n，是n的倍数，矛盾.若a2k+1=-n，同理可得矛盾结论.

原题得证.

总结：本构造法证明中，满足条件：m＞2时，若am＞0，则必存在1≤i1，i2，…，it＜m，使得aij＜0（j=1，2，…，t）且am= -（ai1+ai2+…+ait）；若am＜0，则必存在1≤i1，i2，…，it＜m，使得aij＞0（j=1，2，…，t）且am=-（ai1+ai2+…+ait）.它保证了，每构造一个数，前面都有若干个与它符号相反的数，这些数与它的和恒为零.这种构造是优美的.F