2022 年高考天津卷导数压轴题的探究

广东省佛山市乐从中学(528315) 林国红

一、题目呈现

题目(2022 年高考天津卷第20 题) 已知函数f(x) =ex−asinx,.

(1)求函数y=f(x)在(0,f(0))处的切线方程;

(2)若y=f(x)和有y=g(x)公共点,

(ⅰ)当a=0 时,求b的取值范围;

(ⅱ)求证:a2+b2>e.

试题的知识方面主要考查导数的运算,函数的切线方程,不等式等相关问题;思想方面主要考查转化与化归,方程与函数等思想. 综合考查考生对函数、方程、导数、不等式等基础知识的掌握和理解,推理论证及运算等方面的能力.

试题分步设问,逐步推进,试题的问题(1),问题(2)(ⅰ)较为简单,本文不作讨论;试题的问题(2)(ⅱ)的综合性较强,较好地达到了考查目的. 试题的思维过程体现了能力立意的命题思想,对于考生运用所学知识,寻找合理的解题策略以及推理论证能力有较高的要求. 本题层次分明,区分度高,作为试卷的压轴题,是一道能突出选拔学生功能的好题.

下面从不同视角,给出问题(2)(ⅱ)的几种证法.

二、证法探析

分析因为y=f(x) 和有y=g(x) 公共点, 故方程有实数解,显然x= 0 不是方程的解,所以只需考虑x>0.

视角1: 绝对值不等式与均值不等式

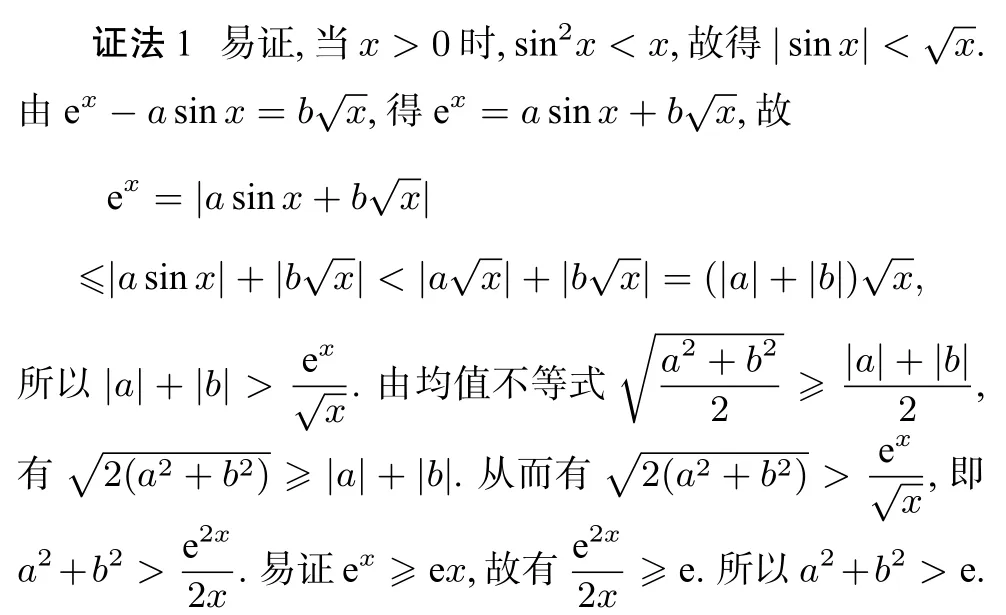
评注证法1主要利用sin2x 0)等. 究其主要原因有三: 首先,此类函数的导数可以和多项式函数结合到一起,体现转化与化归思想;其次,此类函数能体现微积分的一个思想: 以直代曲,无限逼近;另外,此类函数与高等数学的级数结合比较紧密.

视角2: 柯西不等式

评注证法2 与证法3 利用柯西不等式进行放缩,思路巧妙,运算量较少,具有直观、简捷的特点. 所以在平时的学习中要善于钻研,重视方法的积累和知识的储备,熟练掌握一些有用的结论,才有可能缩短思维的长度,提高效率,达到事半功倍的效果.

视角3: 主元法

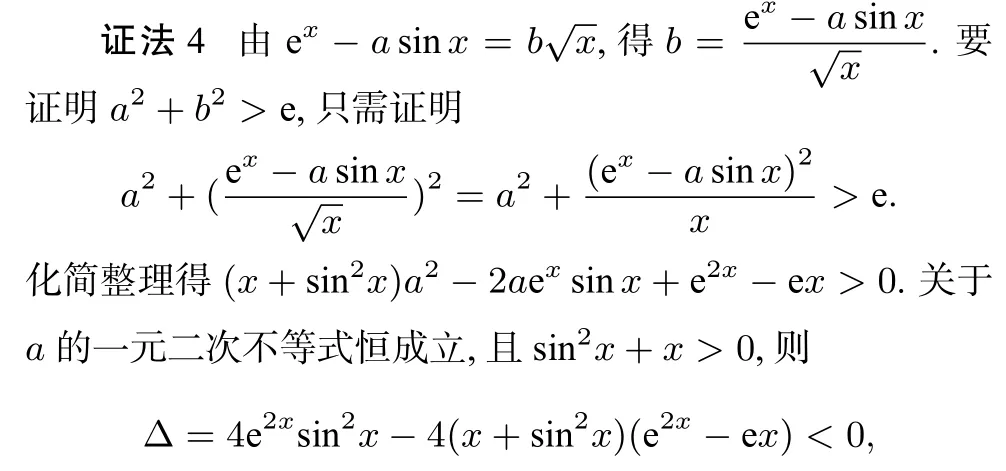
评注在处理不等式有关问题时,若题目中有多个变量,且以x为主元解答较困难时,可以尝试改变分析问题的角度,重新确立主元,排除参数的干扰. 这样往往会有“山穷水尽疑无路,柳暗花明又一村”的豁然开朗之感, 从而可化繁为简,化难为易.

视角4: 直线方程与点到直线的距离

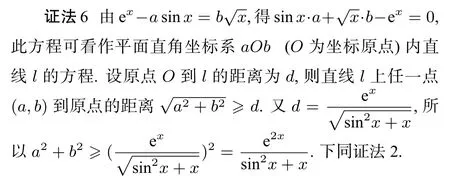
评注本证法数形结合,思路独特,过程简捷,明了,令人叫绝. 数形结合思想的应用十分广泛,著名数学家华罗庚先生曾用一首诗完美的阐述了数形结合的价值和本质,即“数形本是相倚依,焉能分作两边飞. 数缺形时少直觉,形缺数时难入微. 数形结合百般好, 隔裂分家万事休. 几何代数统一体,永远联系莫分离. ”在运用数形结合解题时,要注意“以形助数,以数解形”,用直观的几何反应抽象的公式,用精确的代数规范几何图形.

视角5: 三角换元与辅助角公式

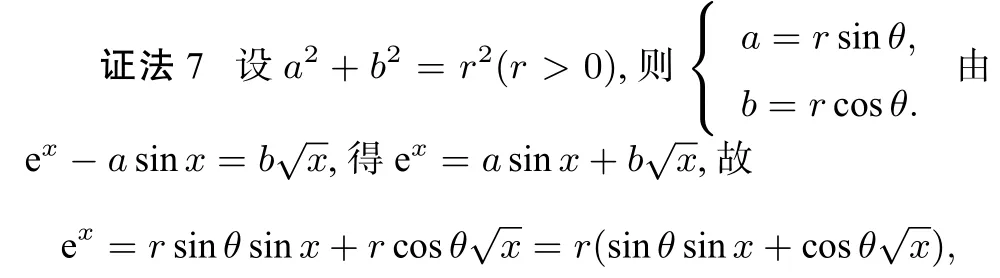
评注本证法利用三角换元,借助三角函数的辅助角公式与正弦函数的有界性进行放缩. 证法新颖,能简化推理和运算过程.

视角6: 反证法与柯西不等式

评注本证法采用反证法,借助柯西不等式,ex>x+1,sin2x

一题一世界,试题的解答分别应用均值不等式、柯西不等式、主元法、三角函数、反证法、数形结合等高中核心知识,证法各具特点,各自精彩.“横看成岭侧成峰,远近高低各不同”,从不同的思维角度分析同一道题目,得到不同的解题方法,一题多解的方式增加了题目涉及的知识广度,体现了知识的横向联系. 从数学知识的角度来看,通过解题发现知识的相互联系,体会知识之间的转化过程,从多角度地思考和发现问题,从而构建知识的网络体系. 因此要对典型的题目要深入挖掘,探求试题背后的思想方法,注重一题多解,力求对所学的知识融会贯通.

三、链接高考

纵观近几年的高考试卷,函数不等式的证明是热门的考点之一,有综合性强,思维量大,方法繁多,技巧性强等特点,特别是以ex,lnx,sinx(或cosx)为背景的函数不等式证明,倍受命题者青睐,常作为压轴题频频亮相. 例如:

四、结语

高考试题是精心之作,每年的高考题在命题角度、题型、难度等方面都进行了充分考量,是知识、能力和思想方法的载体,是命题思想、命题理念的程序化展现,具有典型性、示范性和权威性. 高考试题有良好的导向性,要了解高考动向、把握高考脉搏,高考试题的研究分析是重要的路径. 因此要充分认识高考题所蕴含的价值,对典型的高考题要深入挖掘,探求试题背后的思想方法,精学一题,妙解一类,进而形成一个条理化、有序化的高效的认知结构,从而提炼出数学思想与方法,使思维得到发展.