巧妙转化，化繁为简

王锦萍

［摘  要］ 基于培养学生解题能力的需要，在初中数学解题教学中，最需要重视的数学思想方法之一就是转化思想. 转化思想有助于学生更好地把握解题过程，寻找反思解题过程的抓手. 转化思想在初中数学教学中有着重要的理论价值，要把这种理论价值变成真正的实践价值，关键还在于组织解题教学. 解题教学的重点是想方设法让学生体验转化思想的过程，并且养成反思的学习习惯. 转化思想，是初中数学解题教学的主要线索，也是学生体验解题过程的主要线索. 转化思想一旦成为解题教学的线索，那解题教学就会变得高效，学生也会收获满满. 这种收获既体现在解题能力上，又体现在数学学科核心素养上. 数学课堂从知识教学走向数学思想方法渗透，最终落实核心素养.

［关键词］ 初中数学；转化思想；解题教学

解题教学是初中数学教学的重要环节，无论是基于现实的应试需要，还是基于数学学科核心素养培养的需要，都绕不开解题教学这一重要环节. 解题教学使得学生所学得的数学知识具有較强的应用性，有助于发展学生的思维. 从现实情况来看，初中学生在数学解题中所遇到的挑战是多方面的. 学生对传统题目的解答效率上不去，新型习题的解答方向难以明确，同一习题出现多种方法时难以做出选择……这些是学生迫切想要解决的问题，但是由于种种客观条件的限制，学生在尝试解决这些问题的时候，所采用的方法就是进行更多的习题训练，这实际上是路径依赖的产物. 对绝大多数学生而言，他们提升解题能力的唯一方法，就是增加习题的训练类型与训练量，如此形成的解题能力，通常体现为迅速识别熟悉题型以及一定程度上提高解题速度等，而这些都不能算是根本的突破.

那么怎样才算是根本的突破呢？当然是指解题思想方法的提炼. 解题思想方法，实际上就是解决数学问题的思想方法，与数学知识学习过程中表现出来的思想方法并没有质的区别，如果非要说有区别的话，那区别就在于这些思想方法运用的场合不同，学生最终形成的直觉不同. 不过这种不同不会产生质的影响，这是因为数学思想方法原本就具有迁移性，数学思想方法的生命力就体现在其能够在多个场合得到应用. 本着这样的思路，并基于培养学生解题能力的需要，笔者认为在初中数学解题教学过程中，最需要重视的数学思想方法之一就是转化思想.

顾名思义，转化思想贵在转化. 转化的目的在于化繁为简、化难为易. 转化的过程也是有技巧的，如果能够让学生在转化的过程中掌握相关的技巧，就可以让学生对转化思想产生认同感，当然也就会有更良好的体验. 近年来笔者在初中数学解题教学中，一直注意转化思想的渗透，摸索出了转化思想的教学方法，现总结出来与同行分享，并期待同行的点评.

转化思想在初中数学解题教学中的理论价值

通常一线教师的教学研究会有两种价值取向. 一种是满足应试的需要，只要能够让学生获得解题能力，在中考中获得分数就行. 在这样的价值取向之下，解题教学的研究重心，一定会放在题型的收集上，以使学生能够高效解答多种类型的题目. 但是这种解题教学有一个缺陷，那就是学生无法形成系统性认识，而且教师难以摸索出一条行之有效的教学途径. 另一种是从理论与实践的角度建立起关于解题教学的系统认识，既关注学生的解题直觉，又重视对学生进行思想方法的渗透. 这样的研究价值取向的缺点在于花费的时间较多、必须进行相对系统的理论学习，还要通过总结与反思来提炼思想方法. 但是其优点也是显而易见的，可以让解题教学变得可持续. 在新课改的背景下，当代教师应关注第二种价值取向.

带着这样的思路来看转化思想，可以发现转化思想是常用的数学思想之一，是指在研究新问题或复杂问题时，把其转化为已知的或比较简单的问题来解决. 因此，从这个角度来看，转化思想在初中数学解题教学中的理论价值，至少应当体现在以下两个方面.

第一个方面，转化思想有助于学生更好地把握解题过程. 对相当一部分初中生而言，数学解题的过程是非常繁杂的. 很多学生在成功解题之后，让他们说出自己是如何成功解题的，他们都会吞吞吐吐、语焉不详. 这倒不是学生不想说，而是他们确实说不出来. 会做却说不出来，为什么会出现这种情况呢？答案很简单，这是因为学生在日复一日的习题训练当中，所形成的是关于熟练题型的解题直觉，通常都处于“知其然，却不知其所以然”的状态，解题方法更多地以默会的形式存在. 转化思想作为最常见的解题思想方法，其优点就在于可以让学生在解题的时候，梳理自身的解题思路. 解题的过程就是从已知走向未知的过程，化解难题的过程就是想方设法化繁为简的过程，无论采用怎样的方法，都可以称之为“转化”. 当“转化”成为学生大脑中的一个明确概念时，无论解什么样的题，他们都会想到“转化”.

第二个方面，转化思想有助于学生寻找反思解题过程的抓手. 很多教师认为解题能力是在学生解题过程中养成的，实际上解题能力更多的是在反思过程中形成的. 有经验的教师，在解题教学中会强调解题要能够从“一道题”走向“一类题”，只可惜这种经验却没有转化为学生的解题智慧. 那么真正的解题智慧是什么呢？应当是让学生在成功解题之后去进行深刻反思. 最简单且最有效的驱动性问题就是：我（指学生）是怎样成功解决这道习题的？只要学生紧扣这个问题进行反思，那么他反思的对象就一定蕴含转化思想. 这时，转化思想就成为学生解题反思的一个重要抓手.

转化思想在初中数学解题教学中的应用分析

通过以上分析可知，转化思想在初中数学教学中有着重要的理论价值. 转化思想的核心在于从未知转化为已知，化繁为简，提高解题效率，发展思维能力. 要把这种理论价值转化为真正的实践价值，关键还在于组织解题教学. 基于上述分析，可以得出的一个初步结论：解题教学的重点就是想方设法让学生体验转化思想，并且形成反思转化思想方法运用的学习习惯.

人教版初中数学教材特别注意对习题的精心选择与编制，其中的大部分例题都能够起到促进学生解题能力提升的作用，还有相当多的例题可以成为转化思想的教学载体. 在人教版初中数学七年级上册“整式的加减”章节最后的综合运用中，有这样一道题：

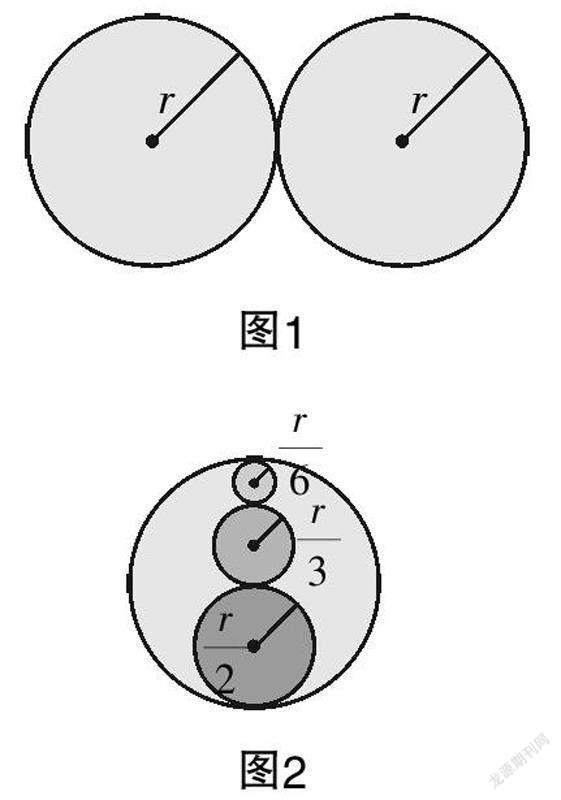
例题呈现 某公园计划砌一个形状如图1所示的喷水池（图中长度单位：m），后来有人建议改为图2的形状，且外圆的直径保持不变. 请你比较两种方案，确定哪一种方案砌出的圆形水池所需要的材料多. （提示：比较两种方案中各圆形水池周长的和.）

很显然，这道题目具有一定的现实意义，其运用了公园砌喷水池这样来自生活的事例. 考虑到初中生的理解能力，这道题目有两个台阶：一是直接给出了图形，而没有用文字来描述这些图形的特征；二是给出了“提示”，告诉学生比较砌水池所用的材料，实际上就是比较周长.

如果意识到这两个台阶的存在，那么在这道题的解题教学过程中，转化思想的体现就有了很大的空间；反之，如果意识不到这两个台阶的存在，那么在这道题的解题教学中，就不容易体现解题过程中的转化思想. 这也提醒一线教师，要想落实转化思想的教学，很多时候就要研究教材题目，发现解题过程中隐含的转化思想，通过对题目的优化与改变，让学生拥有体验转化思想的机会. 在本题的解题教学中，笔者所做的优化与改变，就是将这两个台阶撤掉. 这样的题目对学生来说有一定的难度. 当学生就更容易进入攻坚克难的状态，这个时候再用图形和提示来帮助他们化解难度，学生就会发现图形和提示具有重要的价值，而图形和提示本质上就是转化思想的载体. 因此，笔者在教学中先向学生提供的是这样一个题干：

例题变形 某公园计划砌两个半径为r且外接的圆形的喷水池；后来有人建议将这两个水池改为艺术形状的造型，即在保留一个圆形水池的情况下，在这个圆形喷水池的一条直径上并排砌三个较小的圆形喷水池，半径分别为r/2，r/3，r/6. 请你比较两种方案，确定哪一种方案砌出的喷水池所需要的材料多.

从文字表述的角度来看，该题的含义与原题是一致的，但很显然这样表述抽象很多，学生必须根据文字的表述，在大脑当中构建相应的表象. 这会让学生遇到第一个困难——理解题意的困难. 这并不是为学生刻意制造困难，实际上是为了培养学生的表象建构能力（本质上就是转换能力）. 很多题目无图且文字极少，学生解决时面临巨大的困难，说到底都是转化能力薄弱所导致的. 因此，设计这种较难理解的题目，可以有效培养学生的转化能力. 当学生在解题过程中感觉到抽象时，教师可以引导学生在草稿纸上画图. 画图的时候允许学生出错，鼓励学生交流，只要学生在体验转化的过程即可. 同样，在学生画出正确的图形之后，也可以交由学生自己去完成问题中从“比较材料多少”向“比较周长大小”的转化.

在学生体验转化思想在解题中的应用之后，教师必须重视后面的反思环节，使学生在反思中发现，通过画图，可以降低题目的难度. 将生活素材转化为数学素材，然后再用数学知识去解答，是学生必须掌握的思想方法. 当学生认识到这些的时候，就是他们认同转化思想、获得转化能力的时候.

转化思想在初中数学解题教学中的应用反思

如果说学生在反思当中可以获得对转化思想的感悟的话，那么教师同样也可以在反思中获得解题教学能力的提升. 美国学者波斯纳特别重视教学反思的作用，他认为反思是促进教师专业成长最重要的动力之一. 那么在反思转化思想在初中解题教学中的作用时，又能得出哪些有益的启发呢？对此笔者进行了认真细致的梳理，形成了如下两点认识.

一是转化思想必须成为初中数学解题教学的主要线索. 教师的教学一定是受教学线索牵引的，很多教师在教学设计的时候，都会有意无意地寻找一条线索贯穿教学的始终. 习题教学尤其如此，只有明确了教学线索，课堂上出现的各种习题才不会像一盘散沙一样毫无章法，学生才能从一道题目自然地过渡到另一道题目. 如果教师将包括转化思想在内的数学思想方法作为解题教学的线索，那么解题教学的过程也会十分清晰.

二是轉化思想应当成为学生体验解题过程的主要线索. 这是站在学生的角度进一步强调转化思想的线索价值，这一点实际上更加重要. 因为当学生在若干个题目的解答过程中，能够体验到转化思想的作用时，才会形成累积效应，才会在一点点积累中，提升对转化思想的认知. 学生对转化思想的认识不是一朝一夕就能形成的，只能在一题又一题的体验中慢慢积累，只能在一次又一次的反思中巩固.

以上两点认识，实际上指向教学的两个方面，当这两个方面结合起来成为教学过程的一体两面时，转化思想在初中数学解题教学中就能真正落地生根. 大量的教学实践表明，转化思想一旦成为解题教学的线索，解题教学就会变得高效，学生也会收获满满. 这种收获既体现在解题能力上，又体现在数学学科核心素养上. 毕竟，从知识教学走向数学思想方法渗透，核心素养就能得以落实.