立足实践操作，发展演绎推理能力

祁倩倩

［摘  要］ 推理是一种常见的数学思维方式，具有将抽象内容具体化，深化学生对知识本质理解的作用. 文章以“证明”的第一课时的教学为例，以教学分析为起点，结合对“观察到的结论并不一定是正确的”“说理是确定实践结论的关键”两部分内容的授课，具体谈谈在初中数学教学中，该如何立足于实践操作，发展学生的演绎推理能力.

［关键词］ 证明；演绎推理；思维

“数学是思维的体操”，是促进学生逻辑推理能力发展的学科. 逻辑推理能力是指学习者能敏锐地分析并思考所遇到的问题，迅速掌握问题核心，并在短时间内做出正确反应的能力. 逻辑推理包括演绎推理、归纳推理与类比推理三种，本文着重探讨的是演绎推理. 这种推理方式以“一般性”为前提，通过推导获得具体结论，它在一惯性与严密性上与其他两类推理方式相比，具有一定的独特性.

教学分析

《义务教育数学课程标准（2022年版）》（下文简称新课标）将数学核心素养定义为学生必须具备且能适应其终身发展与社会需要的关键品质与能力，并明确了六大素养，提出了“四基与四能”“三会”等要求［1］. 实践证明，数学实践操作以“做”为支架，让学生通过动手动脑自主发现一些数学结论，同时教学实践操作具有显著的直观性，便于学生理解核心知识，可以取得口头教学所无法比拟的教学效果.

数学实践操作主要以问题为起点，将结论设为操作的最终目标，是展示知识形成过程的一种教学活动. 其内容选择并不拘泥于教材，还可以源于生活，是数学课程必要的补充. 学生在数学实践操作中，除了能直观地看到知识本质，体悟数学思想方法，还能积累学习经验，为后续研究奠定基础［2］.

学习本节课之前，学生已经具备了一定的合情推理能力（通过探索发现结论），在此基础上培养他们的演绎推理能力具有较强的可操作性. “证明”的第一课时，教学目的在于让学生发自内心地感受“证明”的强大力量，为学生演绎推理能力的形成奠定基础.

教学实录

1.获得的结论并不一定是正确的

纵然实践操作有着得天独厚的教学优势，我们通过实践操作所获得的结论并不一定是正确的，这就需要我们具备敏锐的洞察力，在演绎推理的过程中学会辨析. 本节课中，师生首先共同回顾“三角形内角和”的操作证明过程，在学生提出“量、剪、拼”的方法后，教师邀请一名学生到黑板上快速用三角形模板进行实操演示.

教师总结并板书：实践操作是认识新事物的重要手段之一.

师：通过操作所获得的结论，通过感官系统所感知到的结论一定都是正确的吗？

生1：不一定.

师：请举个例子说明一下.

演示1 如图1，一位学生画了两幅大小圆的图. 观察两幅图，学生一致认为图1（2）中间的大圆比图1（1）中间的小圆大. 当画图的这位学生将两幅图叠合在一起时，大家惊讶地发现图1（1）中间的小圆竟然大于图1（2）中间的大圆.

演示2 如图2，判断两根线段的长度是否相等. 在没有虚线的情况下，大家都认为前面那根线段比后面那根线段长，而实际上两根线段一样长.

师：通过以上两个例子，我们能获得什么道理？

生2：通过肉眼观察所得到的结论，有时候受参照物的影响会出现偏差.

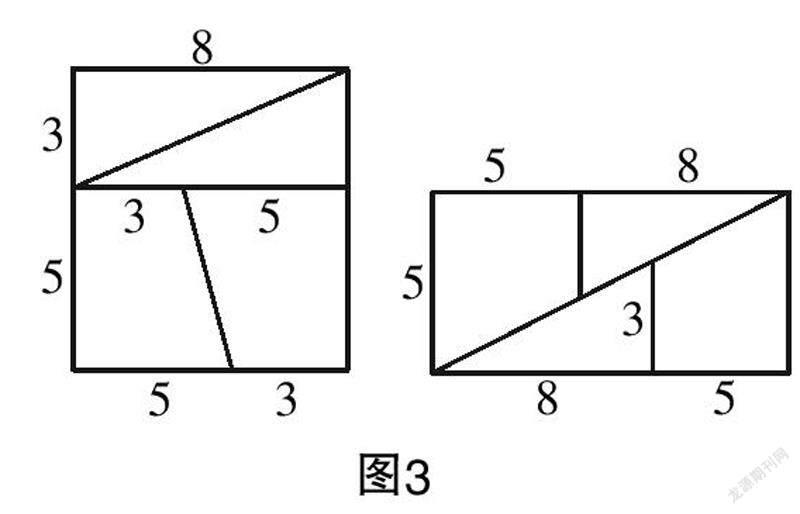
师：很好，那么我们在数学实践操作过程中所获得的结论是否可靠呢？现在请大家做如下操作，将一个边长为8 cm的正方形，剪拼成一个5 cm×13 cm的长方形.

演示3 如图3，学生以小组合作学习的方式进行画图、剪拼. 实验结束后，学生发现了一个问题，即正方形的面积为8×8=64 cm²，而拼成的长方形面积却是5×13=65 cm2，那么这多出来的1 cm2是从哪里来的呢？

教师为学生提供了一张边长为80 cm的大正方形，通过剪拼后，学生恍然大悟，原来拼成的长方形中间存在一个缝隙. 至此，问题就迎刃而解了.

教师板书：实践操作所获得的结论并不一定是正确的.

三个实例，刷新了学生原本对实践操作的认识. 不少学生原本认为自己亲眼所见、亲耳所闻的一定是真理，而事实告诉他们：参照物不一样，感官对同一信息会产生不一样的反饋. 如何避免这种问题呢？需进行进一步说理与证明.

2. 说理是确定实践结论的关键

如果说实践操作是说明事实的过程，那么论证是验证该事实是否正确的重要渠道. 反观之前所接触过的“论证三角形内角和”问题，学生通过操作获得相应结论后，教师还会对为什么三角形的内角和为180°进行补充说明，此时的补充说明就是说理的过程.

教师板书：实践操作所获得的结论，需要经过论证才能确定其是否成立.

例1 某小区有一条长、宽分别为a m、b m的长方形草坪，现在准备在这块草坪中间铺一条鹅卵石的小路，预计路宽为1 m. 设计师提出了直路（见图4）与曲路（见图5）两种方案，面对这两种方案，工程师产生了争执.

甲工程师：直路的方案比曲路方案好，因为直路比曲路省材料.

乙工程师：我认为曲路的方案好，有艺术感，而且曲路与直路的面积是一样的，因此耗材也一样.

师：你们认同哪位工程师的观点？说明理由.

学生经思考后，提出曲路确实更具美感，适合用在小区内. 但直路与曲路的面积是否一样，需要研究一下. 从两条小路的面积来观察，图4的直路面积为1×a=a m²，但图5中曲路的面积该怎么求呢？学生一致认为这是个棘手的问题.

教师要求学生通过小组合作的方式来探寻答案. 从巡视中发现，学生无从下手，于是教师适当地加以点拨：长方形草坪的面积为ab（m²），除去草坪部分的面积就是路的面积，如果从路的角度无法获得结论，就从草坪面积着手.

在教师的点拨下，立即有学生发现路的宽度恒为1，草坪被路分成了两半. 若将两块草坪的面积合并（学生操作，剪拼），则得出以下结论：S_曲路=ab－a（b－1）=a m². 由此可确定曲路与直路的面积是一样的，也就是说乙工程师的意见是正确的. 此即为说理的过程.

师：本题的解题关键在于求曲路面积时，要关注到剩下草坪的面积与路的面积的和是ab. 解题时，思维不要局限于求路的面积，还可以转化为求草坪的面积. 这体现了一种重要的数学思想方法“转化思想”，应该说这个结论是本节课的一个重要收获.

教师板书：转化思想.

师：刚才，我们用说理的方式证明了在几何图形中两条不同形状小路面积的关系问题，从中大家都感受到了说理在数学学习中具有的力量. 其实，说理在数学学习中无处不在，接下来，我们通过一个代数的例子来感受说理对数学学习的影响.

例2 教师用PPT展示代数式：x²－2x+2.

师：在这个代数式中，当x取值发生变化时，值也会相应地发生变化，但究竟是怎么变化的呢？我们都知道x可以取的值太多了，我们该从什么角度去取值并判断结论的变化范围呢？

生1：可以随便取几个试试，或者从正数、负数与零中各取几个试试.

师：那就请大家分别从这几类数中取值看看.

学生自主取值存在一定的个体偏好，如一位学生分别取了2，6，10， 0，－2，－4，－8. 这位学生所取的值，都是整数且为偶数. 真是无心插柳柳成荫，这种取值方法是教师没有预设到的，因此产生了不少意料之外的猜想.

教师将这位学生的取值投影到黑板上，并要求大家建立一个表格（见表1），将数据填入表格后进行分析.

师：大胆的猜想是获得伟大发现的基础. 现在请观察你们填写的表格，并对x²－2x+2的取值范围提出相应的猜想.

在教师的鼓励下，学生经过分析获得如下猜想：①x²－2x+2的值必然为偶数；②该式的值必然为正数；③该式的值必然为整数；④x²－2x+2的值必然大于等于2，等等.

教师要求学生辨别这些猜想的正确性. 有学生提出，可以从反面进行论证，即举反例.

师：既然提到了举反例的方法，现在请大家再取几个特殊值来看看以上猜想是否正确.

生2：当x为1时，该式的值为1. 此时，新的猜想又出现了，即x²－2x+2的值必然大于等于1.

師：这个结论是否正确呢？咱们再来取值看看.

此时，学生提出了困惑：x的值不可能全都取到呀，这怎么判断呢？

问题又回到了原点.

师：如果从完全平方公式着手分析呢？

生3：将式子x²－2x+2进行变形可得（x－1）²+1，从这个式子来看，x可以取任意值，且（x－1）²≥0，此时问题也就迎刃而解了，即（x－1）²+1≥1.

师：说理是验证操作所获得的结论是否正确的重要方式，这也是下节课我们要着重研究的问题——证明.

此时，学生被说理的力量深深震撼，通过式子的转化与演绎推理方法的应用，答案浮出了水面. 此过程，教师顺应学生的思维，强调：判断一句话是错误的可以从“举反例”的角度去证明. 判断一句话是正确的则可以从“严密说理”的角度去证明［3］.

教师板书：实践操作得到的结论，离不开说理论证的过程.

教学思考

1. 结合实情调整教学顺序

本节课教学从预设到生成并没有完全遵循教材内容的顺序，而是结合新课标所提出的“引导学生从合情推理到演绎推理发展”的要求，根据学生的实际认知水平进行了教学内容的调整. 本节课的重点放在“为什么要说理”，也就是进行演绎推理的理由上. 此过程为观念形成过程，对后续学生的学习具有重要影响，因此教师耗费了大量的时间与精力在这个问题上.

事实说明，在解决了“为什么要说理”的基础上引导学生充分感受证明的力量是正确的选择，一节课下来，演绎推理的重要性与证明的力量在每个学生的脑海中生根发芽. 因此，结合实际情况微调教学顺序，不失为一种良好的教学方式.

2. 结合课标调整教学方案

新课标的落地，引发了教育界的一股研究热潮，尤其是“三会”要求的提出，让广大教育工作者不得不思考接下来的教学方向与方案. 究竟该如何才能让学生通过课堂教学“会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界”？

研究发现，教师应用现成的导学案、教案与课件等，疏于深入思考，会导致教学流于形式，学生也无法感受到教师的良苦用心，更无法做到“三会”.

本节课，从教学内容上来分析，主要有三个模块，分别为：①引导学生认识到实践操作是认识一般事物的基本手段；②带领学生感知，实践操作所获得的结论并不一定是正确的；③让学生体验，通过实践操作所获得的结论只有经过说理的过程，才能确定其是否成立. 其中，说理存在两种方式，一种为举反例，还有一种为步步有据.

因此，教师制订在教学方案时，需从以上几部分内容着手进行分析，并结合学生的实际认知水平，而非不加思考直接取用现成的课件. 基于学生实际情况，在本节课中笔者将前两个模块合并在一起教学，使得课堂充满灵气.

3. 结合预设促进课堂生成

课堂预设与生成是相辅相成的关系，因为学生的思维是动态变化的，所以真正的课堂是动态的. 教师只有在课前做好充分预设，才能在课堂上遇到“意外”时，灵活地采取应对措施，让课堂充满智慧. 这种状态下的课堂能有效促进教学相长.

探讨x²－2x+2的取值范围时，虽然教师做了精心预设，但学生特殊的取值，出乎教师的意料. 此时教师并没有避开这位学生特殊的取值，而是顺应学生思维往下探讨. 这种随机应变的能力是教师综合素养的体现，也是尊重学生的体现，学生在此过程中充分感知到证明的作用与力量.

综上，在本节课的教学中，教师没有完全照本宣科，也没有急于求成地简单告知，而是让学生亲身经历了实践操作后思维的发生发展. 师生通过几个实例证明了“实践操作所获得的结论并不一定是正确的”，这个观点不仅对学生数学学习具有深远的影响，而且对于学生的“三会”也有重要影响. 本节课，学生充分认识到演绎推理的重要性，通过推理触碰到了知识的本质，而课堂也因为演绎推理，更具内涵.

参考文献：

［1］ 中华人民共和国教育部.义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.

［2］ 董林伟. 初中数学实验的理论与实践研究［M］. 南京：江苏科学技术出版社，2013.

［3］ 史宁中. 试论数学推理过程的逻辑性：兼论什么是有逻辑的推理［J］. 数学教育学报，2016，25（04）：1-16，46.