借助数轴整体勾联丰盈数感
——《真分数和假分数》教学设计与思考
2022-12-28雷子东曾秀晓
文|雷子东 曾秀晓
【教学过程】
一、猜数游戏,思维卷入
师:同学们,这是一条数轴(如图)。这点表示0,这点表示100,猜猜看,那个点的位置代表多少?

学生猜测之后,教师出示30所在的点,继续让学生猜那个点表示多少?
生:这一段表示30,我想这里应该有2 个30,所以我认为是60。
评价:30、30 地数,这种方法真好!
【设计意图:课一开始就让学生的思维卷进来,主动用单位度量的思维方式开启本节课的学习,为下面从单位度量的角度认识真分数和假分数做好铺垫。】
二、操作体验,探究新知
学习活动一:认识真分数、假分数和带分数
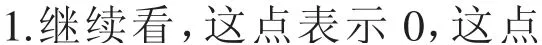



教师呈现分数,学生一一判断。
师:怎么知道自己的猜测对不对?
学生自学书本,再汇报交流。
师:哪些是真分数?为什么?

师:哪些是带分数?

小结:这就是我们这节课要学的真分数和假分数。(出示课题)
反思:这些分数有什么相同点?为什么分母都是4?
总结:都是把1 看作一个整体,平均分成了4 份,所以分母都是4。

学习活动二:感受区间范围,发展数感
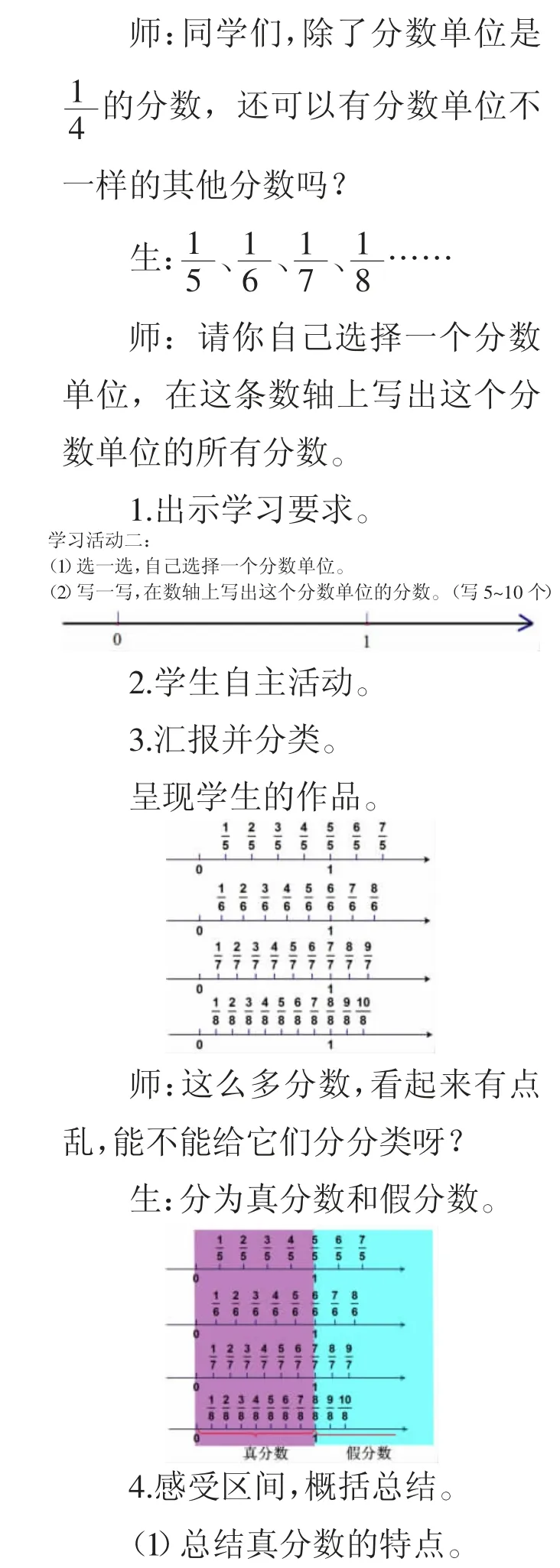
师:真分数都在哪儿呢?关于真分数,你有什么发现?
生1:真分数都在0~1 之间。
生2:真分数的分子小于分母。
师:真分数写得完吗?你能用最简洁的方式把所有真分数都表示出来吗?

师:那么假分数呢?假分数有什么共同特点?谁能用最简洁的方式概括假分数?

(3)总结带分数的特点。
师:关于带分数,你有什么发现?
生1:带分数的范围和假分数的范围是一样的。
生2:假分数都可以化成带分数,带分数也都可以化成假分数。
生3:不对,有些假分数不能化成带分数,只能化成整数。
小结:分子不是分母倍数的假分数都可以化成带分数,带分数都可以化成假分数。
【设计意图:此环节通过小组活动,学生自选一个分数单位,写出它的真分数和假分数,通过多维建构深入认识假分数,感受真分数和假分数的区间,概括出真分数和假分数的特征,理解假分数和带分数之间的关系,发展学生的数感。】
三、素养练习,沟通联系
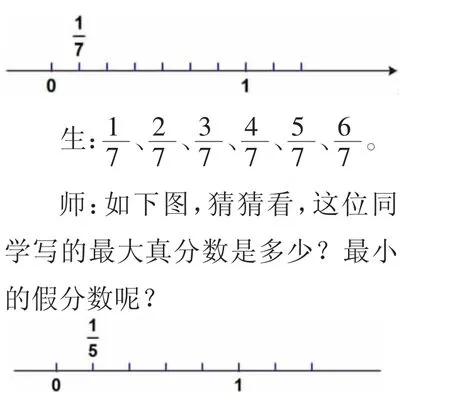
练习1:看图猜一猜。
师:如下图,猜猜看,他写出了哪些真分数?

练习2:挑战易错题。
师:同学们,老师这里有一道分数的易错题,你们敢接受挑战吗?
把一个图形看作单位“1”,下图表示( )。
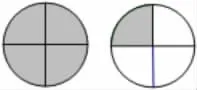
师:猜猜看,其他做错的同学可能会怎么写?
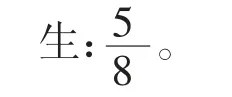
师:我们来猜猜他是怎么想的?避免我们以后犯这样的错误。
生:他是把2 个图形看作单位1,我们应该把一个图形看作单位1。
师:(追问)还有谁有想说的?

【设计意图:练习1 充分利用在学习活动二中生成的素材,通过教师遮一遮,学生猜一猜,从教师提问到学生提问,体现了练习的灵动性。练习2 是一道典型易错题,引发学生进一步思考与说题,引导学生的思路越辩越明晰。】
练习3:沟通分数与整数,分数与小数的联系。
(1)写出下列整数所表示的分数。

师:你有什么发现?
生:整数可以表示成分子是分母倍数的假分数。
(2)写出下列小数所表示的分数。

师:你有什么发现?
生:小数都可以写成分母是10、100、1000 等的分数。
师:同意吗?同学们课后可以继续思考。
【设计意图:知识重在求联。练习3 用数轴沟通整数与分数之间、小数与分数之间的联系,让学生自主发现并总结出分数与整数、小数之间的密切联系,培养学生观察、发现、抽象概括的能力和数感。】
四、回顾总结,提出新的问题
师:学了这节课,你对分数有什么新的认识?
师:你还有什么疑问吗?

【课后反思】
1.化被动为主动,自主重构对分数的认识。
整节课充分放手让学生进行自主学习。课始用猜一猜的游戏,调动学生思维,主动用计数单位度量的方法去猜测。课中用两个大活动,给足学生思考与探索的空间,鼓励学生自主学习。尤其是真分数、假分数和带分数的认识,先启发学生:这些分数在名称上是否也有所不同?再自主看书解惑。一改传统的由教师告诉学生的教学方式,让学生自己打开课本自学获取新知,再由学生汇报,充分体现了学习的自主性。本课始终凸显学生主体,尊重学生自主感知,层层递进,重构对分数的认识。
2.变单一为整体,整体建构数的体系。
本课以数轴为抓手,多维建构学生对数的认识。横向沟联,认识真分数和假分数。纵向沟联,沟通假分数和带分数的关系,沟通假分数与整数的关系,沟通真分数、假分数与小数的关系。纵横交织,使知识不再是单一知识点的学习,而是连点成线,以点带面,整体建构数的体系。
3.重知识更重素养,发展学生的数感。
本节课始终把发展学生的数感放到首要位置。课始引导学生在数轴上合理猜测,数形结合,以用促学,发展学生的数感。在概括真分数和假分数的特点时,把多条数轴放在一起,对比发现真分数、假分数在数轴上的特点,学生不再是记住抽象的文字描述,而是结合具象的图建立对真分数和假分数的大小认识。在练习中继续利用数轴进行沟通联系,有效落实本节课的核心素养:数感。
