聚焦主题拓展实现算理融通——特级教师蒋守成《铺地锦》教学片断赏析

文刘 留

“你知道吗”是苏教版小学数学教材中的一类“主题栏目”，起到拓展本单元教学内容和弘扬数学文化的作用。如何有效开发教材中的“主题栏目”，放大数学学科育人价值是亟需我们探索的话题。特级教师蒋守成提出“主题拓展教学”主张，基于某个主题将“你知道吗”“动手做”等栏目开发成数学拓展课，帮助学生突破原有的认知边界，促进数学对于人的整体培育。笔者有幸聆听了特级教师蒋守成的《铺地锦》一课，深受启发。

●片断一：故事增趣，激发主动探究的欲望。

1.故事导入，阐述“铺地锦”的时代背景。

师：同学们，今天的数学课我们一起听听民族英雄戚继光的故事，他创建了一支伟大的军队“戚家军”，你瞧！（课件出示）

师：戚家军以36 人为一旗，在一次战争中，戚继光将军派出了72 旗迎战敌军，请你帮戚继光将军算算一共派出了多少士兵？

生：可以用36 乘72，通过列竖式算出来一共有2592 名士兵。

2.问题激趣，唤醒对“铺地锦”的探究欲望。

师：同学们很快就通过列竖式计算出了结果，但是大家不妨想一想在戚继光的时代有没有“列竖式计算”呢？

生：我认为没有，当时的人们应该还不会列竖式计算。

师：虽然戚继光将军不会“列竖式计算”，但是他有自己的一套方法，大家能看懂他的算法吗？

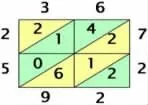
师：请同学们思考两个问题，第一个问题：两个乘数和积分别写在什么地方？第二个问题：戚继光将军是如何算出2592 的？

生1：戚继光将军先画了一个长方形，将乘数36 写在长方形的上面，乘数72 写在长方形的右边，2592 写在长方形的左边和下面。

生2：戚将军先算2 乘6 得12 写在右下角，再算6 乘7 得42写在右上角，然后算2 乘3 得6写在左下角，最后算十位上3 乘7得21 写在左上角，将它们斜着相加，就能算出来结果是2592。

师：两位同学用自己的语言讲出了戚继光将军的运算方法，蒋老师好奇的是为什么右下角填“12”，而左下角却填“06”呢？

生：那是因为2 乘3 得6，6是一位数，所以左下角的方框里只能写成“06”。

师：这下我有点明白了，原来方框里的数是两个乘数十位和个位上的数相乘算出来的。明朝时期人们从平日里织的绸缎、锦缎中获得灵感发明了这种算法，便给它起了一个非常好听的名字———“铺地锦”，用“铺地”的方法算乘法。

【赏析：蒋老师将“铺地锦”算法融入到民族英雄戚继光的故事中，阐述了该算法的时代背景，古代算法至今依然熠熠生辉存在思考价值。那么到底有怎样的价值呢？蒋老师讲述的故事产生了悬念，学生满怀好奇心自然地经历了观察、思考和表达“铺地锦”算法的全过程，并尝试用自己的语言讲述对算法的理解。这类“主动研究型”的课堂教学值得我学习，既实现了数学文化传播，又在学生心中播下一颗“主动学习”的种子。《义务教育数学课程标准（2022 年版）》指出：学生的学习应是一个主动的过程，认真听讲、独立思考、动手实践、自主探索、合作交流等是学习数学的重要方式。蒋老师用实际行动践行着新课标的要求，在探索算法的过程中帮助学生将“铺地锦”与之前的数学学习建立起联系，充分激发学生主动探究“新算法”的欲望，从最接近学生的起点出发走向最远的终点。】

●片断二：对比不同算法，凸显内在关联。

1.初次对比，强调“满十进一”的重要性。

师：请你用刚学的“铺地锦”求出这两道乘法算式的答案。

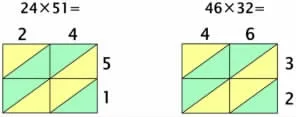
生：我算了第一道题，先在“地锦”中算出1 和4 的乘积写成“04”，4 和5 的乘积写成“20”，1和2 的乘积写成“02”，2 和5 的乘积写成“10”，再斜着全部相加得到1224。

师：对于第二道题，蒋老师发现了大家有两种不同的答案。有的同学算出来是1472，还有的同学算出来是13172，你们认为哪个答案是正确的？说说你的想法。

生1：用“铺地锦”的方法算出十位上分别是8、1 和8，全部斜着相加得到17，十位上满10 应该向百位进1，得到1472 而不是13172。

生2：我觉得13172 肯定不对，将46 看作50，32 看作30，可以估算出46×32 大约是1500,而不是一万多。

师：没错！“铺地锦”的算法也要遵循“满十进一”的计算原理。

2.再次对比，凸显不同算法之间的联系。

师：在运算过程中，我们延伸“铺地锦”算法得到了下面两种不同的列竖式计算方法，你能看懂它们吗？（课件出示）

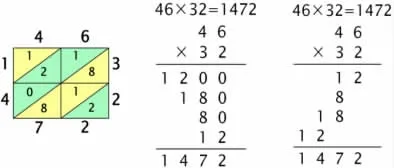
生1：第一种竖式计算是先算十位，再算个位，和我们平时学习的列竖式运算顺序相反。十位上30 乘40 等于1200，30 乘6 等于180。个位上2 乘40 等于80，2 乘6 等于12，全部相加等于1472。

生2：第二种竖式计算类似“铺地锦”，先算“右下角”，2 乘6等于12；再算“左下角”，2 乘4 等于8；然后算“右上角”，3 乘6 等于18；最后算“左上角”，3 乘4 等于12。

生3：我还发现了第一种竖式计算在运算过程中没有省略0，而第二种省略了0。

生4：第一种竖式计算是从高位算起，第二种是从低位算起，它们的运算顺序不同。

师：通过大家的交流，可以发现你们对于以上几种算法的认识已经很充分了。“铺地锦”算法是流行于我国明朝时期的算法，而第一种竖式计算是印度人所使用的算法，第二种竖式计算则是我国台湾省所使用的算法，它们貌似不同，背后都有着相似的道理！

【赏析：主题拓展的本质不是“拼盘”，而是“融合”。蒋老师通过算法对比制造了学生优化算理认识的“关键事件”。首次对比中，学生开展了关于“铺地锦”算法的迁移运用，得到“13172”和“1472”两种答案，他们依据已有经验敏锐地辨别出“13172”这个答案的不合理性，深刻体会到“铺地锦”算法依然要遵循“满十进一”的计算原理，古今算法在本质上一脉相承。再次对比中，课件呈现运用“铺地锦”算法、印度算法、中国台湾算法计算同一道题的过程，学生发现明明运算顺序不同———有的从高位算起，有的从低位算起，却得到了相同的答案。这对于刚学完“笔算两位数乘两位数”的学生来说无疑是认知方面的巨大冲击，打破了其脑海中关于笔算顺序的“原有桎梏”，获得了关于笔算方法的“全新理解”。学生反复思考后发现这几种算法都是先按照一定顺序将各个数位上的数依次相乘得到若干个千、百、十和一，然后基于相应计数单位的累加算出最终结果。蒋老师以此基础支架打通不同算法之间的“隔断墙”，保留算理认识的“承重墙”，实现法与理的相融共生，算与术的交相辉映，让学生在更广阔的运算空间里徜徉。】

●片断三：挖掘算理本质，实现触类旁通。

1.在实践应用中丰富对“铺地锦”的理解。

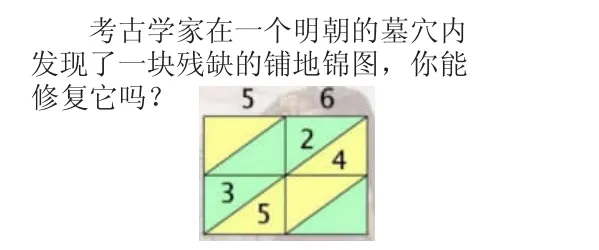
生：我们可以根据积反过来推算乘数是多少。先用24 除以6得到4，再用35 除以5 得到7，说明另一个乘数就是47。紧接着56和47 相乘，算出右下角应该填42，左上角应该填20，算出来积是2632。

师：算得有理有据，如果我们在“地锦”的下面再加上一行呢？右边再加一列呢？

生：那么我们就可以用它来算“三位数乘三位数”是多少。

师：国外还将这种算法称作“格子算法”，本质上和明朝的“铺地锦”算法是一回事。请你再说一说这种算法背后的道理。

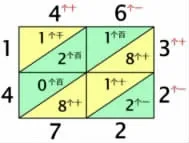
生1：乘数46 表示4 个十、6个一，乘数32 表示3 个十、2 个一，先将其依次分别相乘，再将运算结果斜着相加，这和现在的列竖式计算是差不多的。

生2：斜着的数都在相同数位上，比如“2 个一”在个位，“8 个十”在十位，“1 个百”在百位，“1 个千”在千位。因为数位相同，所以这些数才能相加，算出最终有几个千、几个百、几个十和几个一。

【赏析：“铺地锦”和“列竖式计算”有着千丝万缕的联系，两者在算理上是相通的，更多体现在表现形式和运算顺序的不同。蒋守成老师积极引导学生辨析复杂的算法，在横向对比中实现举三反一，寻求共通的算理，以理驭法直抵数学理解的新境界——学会系统地思维。“融通算理”是主题，“铺地锦”是载体，致力于帮助学生走好数学运算的“后50 公里”。】

2.在算理融通中实现对“不同算法”的触类旁通。

师：再给大家介绍一种“画线法”，或许你对“铺地锦”又会有新的认识，哪位同学看明白这种算法了？

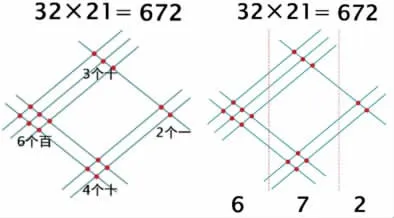
生：它是用五条直线（三条+两条）表示32，三条直线（两条+一条）表示21，直线相交表示两数相乘的过程，将点数竖着相加就能得到各个数位上的数是多少。

师：看来不论是“铺地锦”，还是“画线法”，都需要将各个数位上对应的数相加。

师：后来人们对“铺地锦”进行改良，发明了“棋盘计算器”。它既是一种工具，让运算更加便捷；又是一种文化，让我们看到前人的智慧结晶。正是算法的不断更新，才有了我们今天常用的算法。未来大家一定能发明更加先进的算法！

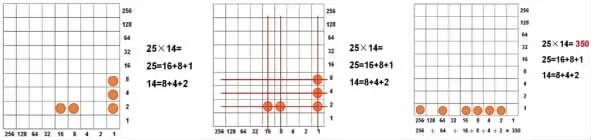
【赏析：教材不是学生的全世界，全世界都可以成为学生的教材。蒋老师向我们展示了如何基于课堂教学在丰富数学学习的同时，帮助学生形成系统化、结构化的思维方式。用整体的眼光看待“格子算法”“画线法”和“棋盘计算器”，它们都需要累加相同的计数单位。在《铺地锦》教学中，学生不仅习得了“铺地锦”算法，更掌握探索新算法、理解新算法的关键能力。一方面，让学生体会到数学是一种工具，让我们的生活更加方便快捷。另一方面，数学也是一种文化传承，从“地锦”“棋盘计算器”到现在的“电子计算器”，彰显出科技进步和出守正创新的奋斗历程。笔者以为本节课真正的价值在于拓宽学生的眼界，放大了“主题栏目”的价值，为我们更好地开发利用教材提供了一种新思路———从照着“书”教转向照着“人”教，促进数学学科对于人的全面培育。】