基于“基础性”考查要求对高考真题的分析研究——以2022年新高考Ⅰ卷第17题数列解答题为例

湖南 张新民

高考命题注重对“基础性”的考查要求，解答题的前几道试题往往设置一些“基础性”试题，旨在考查学生的基础知识、基本能力和基本素养，包括全面合理的知识结构、扎实灵活的能力.这些试题看似素材质朴、背景平淡，但往往平中蕴奇，有着丰富的思想方法内涵，反映出数学本质性的东西，多角度进行分析、探究，对提高数学思维能力大有裨益.2022年新高考Ⅰ卷第17题的数列解答题就是基于“基础性”考查要求的一道优质试题，本篇以该试题为母题，从母题变式、推广及知识联系等方面进行分析研究.

一、母题呈现

(1)求{an}的通项公式；

二、母题分析

试题以基础知识、基本方法、基本数学思想的面目对数列解答题进行考查，试题设置两小问：第(1)问利用题设所给等差数列的条件以及数列“和”与“项”的关系转化为递推式，运用累乘法或构造常数列求出数列的通项公式，这一小问是该道试题的重点部分，需要运用分类讨论和化归与转化等数学思想及累乘法，其中还考查思维的全面性；第(2)问依据第(1)问求得的通项公式，进行裂项求和，然后“放缩”证得结论.试题虽然是试卷中首道解答题，但对数学抽象、逻辑推理、数学建模及数学运算等数学核心素养要求是比较高的.透过试题表象，可以看出命题者对数列解答题命题的深层次思考.

三、母题解答

解法1(累乘法+裂项相消法)：

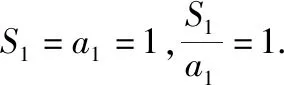
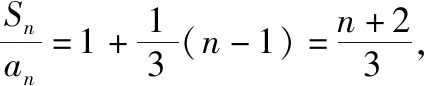
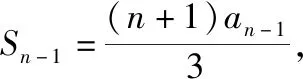
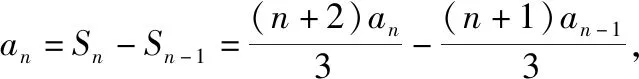
整理得(n-1)an=(n+1)an-1，

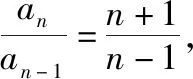
显然对于n=1也成立，

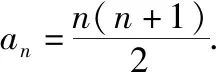
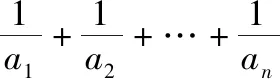
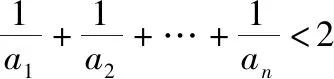
点评：对于第(1)问，利用数列“和”与“项”的关系转化为递推式后，运用累乘法求得an后，需要注意的是不要忽视对于n=1是否成立的验证.

解法2(构造常数列+裂项相消法):

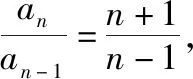
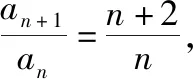
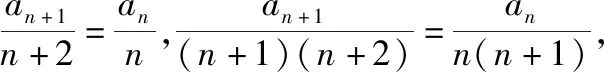
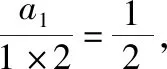
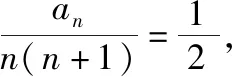
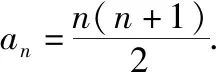
(2)同解法1.

点评：对于第(1)问，首先利用数列“和”与“项”的关系转化为递推式，变形后，通过构造常数列求出数列的通项公式.

四、考查模式

数列是高中数学的核心知识，也是新高考卷解答题中必考的基本内容之一.新高考Ⅰ卷已启用三年，这三年对数列解答题的考查均以考查基础知识、基本方法、基本数学思想的面目出现，试题处于17或18题的位置.试题设置两问：第(1)问求数列的通项公式，主要考查基本量思想的应用、数列有关性质或数列递推关系；第(2)问设置数列求和或与数列通项、前n项和等有关的数列不等式证明、求参数的取值范围等问题.其中“数列求和”是命题的“主旋律”，方法有直接利用求和公式、裂项相消、错位相减、分组求和或分段求和等，这是数列解答题的重点考查方向.下表是2020～2022年新高考Ⅰ卷对数列解答题的考查一览，新高考Ⅰ卷对数列解答题的考查特点由此可窥见一斑.

表 2020～2022年新高考Ⅰ卷数列解答题考查一览

笔者预测2023年新高考Ⅰ卷对数列解答题的考查风格总体上会继续沿用现有模式.从命题形式上看，近年来新高考Ⅰ卷刻意避开“结构不良”的命题形式，尽管在近几年各地的新高考模拟卷中数列解答题的结构不良试题出现的频率很高，命题较多，但新高考Ⅰ卷对以结构不良题型出现的数列解答题还未曾涉及，而数列却是作为命制结构不良试题最佳的素材和载体，因而预测2023年新高考Ⅰ卷命制数列结构不良试题的可能性很大，希望新高考Ⅰ卷地区的教师在指导复习备考时予以关注.

五、母题变式

(1)求{an}的通项公式；

和母题一样，对于第(1)问，也是用两种方法分别来解答.

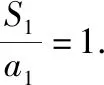
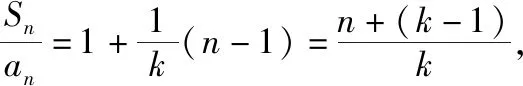
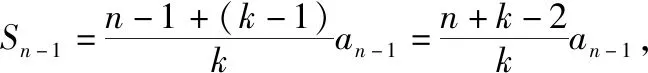
整理得(n-1)an=(n+k-2)an-1，

因为a1=1，且与组合数公式相联系，

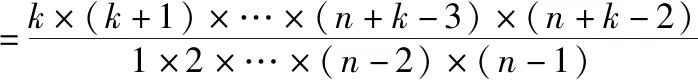
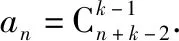
所以当k≥3时，

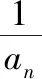
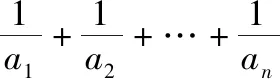
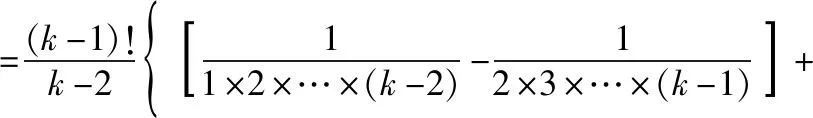
等式左、右两边分母同乘以(n+1)(n+2)(n+3)×…×(n+k-2)，

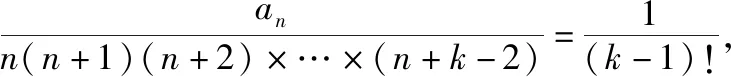
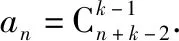
(2)同解法1.

点评：变式1将母题延伸、推广到一般情形，运用数列知识并结合计数原理中的排列数、组合数及其变形推导、证明结论，抽象程度高，逻辑思维能力强，需要有较强的运算求解能力，很好地考查了数学抽象、逻辑推理、数学建模及数学运算等数学核心素养.

考虑到母题的第(2)问是运用裂项相消法求和的，这里在直接给出数列{an}的递推关系的条件下，(1)利用累乘法求通项；(2)考查利用错位相减法求和，则有：

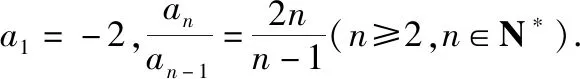
(1)求{an}的通项公式；

(2)证明：a1+a2+a3+…+an≤-2.

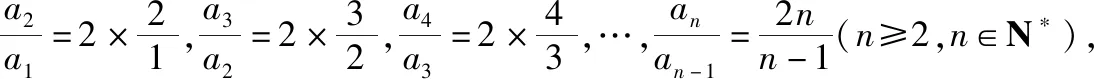
因为a1=-2，所以得an=-n·2n(n≥2，n∈N*).

又a1=-2符合上式，故数列{an}的通项公式为an=-n·2n.

(2)设数列{an}的前n项和为Sn，即Sn=a1+a2+a3+…+an.

由(1)知Sn=-(1×2+2×22+…+n·2n)，

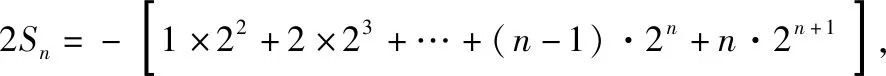
两式相减，得Sn=2+22+23+…+2n-n·2n+1=2n+1-2-n·2n+1=-2+(1-n)·2n+1≤-2.

故a1+a2+a3+…+an≤-2得证.

考虑到裂项相消法求和的多样性，这里将母题第(2)问的裂项相消法求和变为“指数型”，则有：

【变式3】已知数列{an}的前n项和为Sn，a1=1，Sn+1=Sn+2an+1，n∈N*.

(1)证明：数列{an+1}是等比数列；

【分析】(1)首先利用Sn与an的关系，得到an+1与an的递推关系，配凑后证得结论.

【解析】(1)因为Sn+1=Sn+2an+1，

所以Sn+1-Sn=2an+1，

所以an+1=2an+1，

所以an+1+1=2(an+1)，

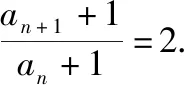
又a1=1，所以a1+1=2，

故数列{an+1}是首项为2，公比为2的等比数列.

(2)由(1)得an+1=2×2n-1=2n，所以an=2n-1，

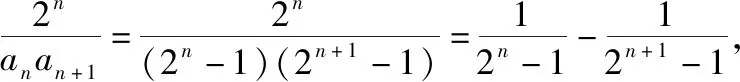
故Tn<1得证.

考虑到命题形式的多样性，这里设置一个结构不良试题，则有：

【变式4】已知数列{an}与正项等比数列{bn}满足an=log2bn(n∈N*)，且________.

(1)求{an}与{bn}的通项公式；

(2)设Cn=an·bn，求数列{Cn}的前n项和Sn.

从①b3=16，b6=128；②b1=4，b5-b1b3=0这两个条件中任选一个，补充在上面问题中并作答．

注：如果选择多个条件分别解答，按第一个解答计分.

【分析】本题是以结构不良试题形式命制的试题，首先从题中所给的两个条件中任选一个，补充到题目中，然后按结构良好试题的模式去作答.

(1)利用已知条件和等比数列通项公式求出数列{bn}的通项公式，再利用已知中两数列关系求出数列{an}的通项公式.

(2)将{an}与{bn}的通项公式代入Cn=an·bn，然后运用乘公比错位相减法求出数列{Cn}的前n项和Sn.

【解析】若选①，

(1)因为数列{bn}是正项等比数列，所以b6=b3q3.

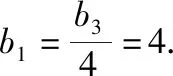
所以bn=b1qn-1=4·2n-1=2n+1.

所以an=log2bn=n+1.

故数列{an}的通项公式为an=n+1，{bn}的通项公式为bn=2n+1.

(2)Cn=an·bn=(n+1)·2n+1，

所以Sn=2·22+3·23+4·24+…+(n+1)·2n+1，

2Sn=2·23+3·24+…+n·2n+1+(n+1)·2n+2.

故Sn=n·2n+2.

若选②，

(1)由b5-b1b3=0，得b5=b1b3.

因为数列{bn}是正项等比数列，设{bn}的公比为q,所以b1q4=b1·b1q2.

因为b1=4，所以q2=4，又bn>0，所以q=2.

所以bn=b1qn-1=4·2n-1=2n+1.

所以an=log2bn=n+1.

故数列{an}的通项公式为an=n+1，{bn}的通项公式为bn=2n+1.

(2)同选①的解法.

六、方法规律

1.求数列的通项公式是高考考查的重点，其中累加、累乘法是求数列通项的基本方法.

(1)累加法

将递推公式变形为an+1-an=c(c为常数)或an+1-an=f(n)，分别令n=1，2，3，…，n-1，n，再将这n个式子相加得an+1-a1的表达式，从而求得数列{an}的通项公式.

(2)累乘法

2.常考的数列求和的主要方法

(1)裂项相消法求和

将数列的各项拆分成两项之差，在求和时一些正负项相互抵消，于是前n项和变成首尾若干少数项之和.裂项相消法求和用得比较多，一般是把通项公式分解为两式子的差，再相加抵消，但是在抵消时，有的是依次抵消，有的是间隔项抵消，特别是间隔项抵消时要注意规律性.另外，要注意的是裂项相消后剩余的正项和负项的项数一样多.

(2)错位相减法求和

若数列{cn}的通项公式为cn=anbn，其中{an}，{bn}中一个是等差数列，另一个是等比数列，求和时一般在已知和式的两边都乘以组成这个数列的等比数列的公比q，然后再将得到的新和式和原和式相减，转化为同倍数的等比数列求和，这种方法就是错位相减法.

(3)分组求和

数列的通项是若干项的代数和，要将其分成几部分来求解.

(4)分段求和

对于以分段形式给出的数列求和问题，先研究各段的规律，然后分段求和后再合并.

七、教学启示