半环同态的若干性质

邵海琴, 梁茂林, 董芳芳

(天水师范学院 数学与统计学院, 甘肃 天水 741001)

1 预备知识

关于软代数的研究已经从软群、软模、软半环、软环和软BCK/BCI代数等不同的软代数系统展开.而关于软半环的研究，自Feng等[1]利用软集合理论，引入软半环，软子半环，软理想和理想软半环等概念，并证明了它们的一些相关性质后，近年来众多学者对软半环理论作了进一步的探讨[2-6].同态和同构是比较代数系统的一种重要方法,在代数系统的研究中有着重要的作用.Rao[7]通过模糊软Γ-半环、模糊软左(右)理想、模糊软Γ-子半环等对模糊Γ-半环同态和模糊软Γ-半环同态进行了研究,得到了它们的一些重要性质;Massa’deh等[8]通过二极Q-模糊软Γ-半环、二极Q-模糊软右(左)理想、二极Q-模糊软Γ-子半环等对Γ-半环同态和二极Q-模糊软同态进行了研究,得到了它们的一些重要性质;Fallatah等[9]利用三极模糊软Γ-半环、三极模糊软右(左)理想、三极模糊软Γ-子半环等对Γ-半环同态和三极模糊软Γ-半环同态进行了研究,得到了它们的一些重要性质;Wang等[10]利用超环上的软超环、理想软超环、软子超环和软理想等对超环强同态和软超环的软同态进行了研究,得到了它们的一些重要性质,并给出了软超环的三个同构定理.同时,对软超环的模糊同态和同构进行了研究,给出了软超环的三个模糊同构定理;邵海琴等[11]利用半环上的软半环、软子半环、软理想和理想软半环等对半环同态进行了研究,得到了半环同态的一些重要性质;邵海琴等[12]利用半拟序、商半拟序、半拟链和商半拟链等对偏序半群的商序同态进行了研究,得到了商序同态的一些重要性质.本文在文献[11]的基础上,利用半环上的理想软半环、完全理想软半环、平凡理想软半环和理想软子半环以及理想软半环间的运算, 对半环同态进行研究.

文中一般的概念和记号均参见文献[1,11].

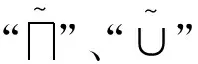
其中

C1=A∩B,α满足对任意的x∈C1,α(x)=η1(x)∩η2(x);

C2=A∪B,β满足对任意的x∈C2,

C3=A×B,γ满足对任意的(x,y)∈C3,η(x,y)=η1(x)∩η2(y).

设(η,A)是半环R上的一个非空软集合.(η,A)被称为R上的一个理想软半环, 若对任意的x∈Supp(η,A),η(x)是R的一个理想.半环R上的一个理想软半环(η,A)被称为是完全的,若对任意的x∈A,η(x)=R.有零元半环R上的一个理想软半环(η,A)被称为是平凡的,若对任意的x∈A,η(x)={0}.设R和S都是半环,(η,A)是R上的一个理想软半环,且φ是从R到S的一个映射.对任意的x∈A,由文献[1]知,可以定义S上的一个软集合(φ(η),A),且有Supp(φ(η),A)=Supp(η,A),这里,

φ(η):A→P(S);φ(η)(x)=φ(η(x))

称(φ(η),A)为(η,A)在φ之下的像集.若φ是从R到S的一个同态满射,则有下列结论.

定理1[1]设φ是从半环R到半环S的一个同态满射,(η,A)是R上的一个理想软半环.那么

1)(φ(η),A)是S上的一个理想软半环;

2)若(η,A)是完全的,则(φ(η),A)也是完全的.

定理1说明,半环R上的理想软半环和完全理想软半环在满同态φ之下的像集(φ(η),A)是半环S上的理想软半环和完全理想软半环,即半环满同态是保理想软半环和完全理想软半环的.

2 主要结论

命题1设R和S都是有零元半环,φ是从R到S的一个同态满射,(η,A)是R上的一个理想软半环.那么

1)若对任意的x∈A,有η(x)⊆Kerφ,则(φ(η),A)是S上的一个平凡理想软半环;

2)若(η,A)是平凡的,则(φ(η),A)是S上的一个平凡理想软半环.

证明1)由定理1中1)知,(φ(η),A)是S上的一个理想软半环.设0R是R的零元,则φ(0R)=0S,其中0S是S的零元.对任意的x∈A,由η(x)⊆Kerφ得

φ(η)(x)=φ(η(x))={0S}

因此,(φ(η),A)是S上的一个平凡理想软半环.

2)由定理1中1)知,(φ(η),A)是S上的一个理想软半环.设0R是R的零元,则φ(0R)=0S,其中0S是S的零元.对任意的x∈A,由(η,A)是平凡的得η(x)={0R},于是由φ是从R到S的满同态得

φ(η)(x)=φ(η(x))=φ({0R})={φ(0R)}={0S}

因此,(φ(η),A)是S上的一个平凡理想软半环.

命题1说明,半环R上的平凡理想软半环(η,A)在满同态φ之下的像集(φ(η),A)是半环S上的平凡理想软半环,即半环满同态是保平凡理想软半环的.

例1取整数半环Z和模n(n∈Z+)剩余类半环Zn.对任意的x∈Z,令

φ:Z→Zn;x

容易证明,φ是从Z到Zn的一个满同态,且Kerφ={nk|k∈Z}.

取A=Z+, 且对任意的x∈A,令

η:A→P(Z);x{nxk|k∈Z}=nxZ.

对任意的x∈Supp(η,A),很显然,η(x)都是Z的理想,因此,(η,A)是Z上的一个理想软半环.

对任意的x∈Supp(η,A),很显然,η(x)⊆Kerφ,因此,由命题1中1)知,(φ(η),A)是半环S上的平凡理想软半环.

再取A=Z+,且对任意的x∈A,令

η:A→P(Z);x{0xk|k∈Z}={0}.

对任意的x∈Supp(η,A),η(x)={0}是Z的零理想,因此,(η,A)是Z上的一个平凡理想软半环,因此,由命题1中2)知,(φ(η),A)是半环S上的平凡理想软半环.

设φ是从半环R到半环S的一个同态映射,(η,A)是S上的一个理想软半环.对任意的x∈A,由文献[11]知,可以定义半环R上的一个软集合(φ-1(η),A),且有Supp(φ-1(η),A)=Supp(η,A),这里,

φ-1(η):A→P(R);φ-1(η)(x)=φ-1(η(x))

称(φ-1(η),A)为(η,A)在φ之下的原像集.

下面讨论半环S上的理想软半环(η,A)在φ之下的原像集(φ-1(η),A)的性质.

定理2设φ是从半环R到半环S的一个同态映射,(η,A)是S上的一个理想软半环,那么(φ-1(η),A)是R上的一个理想软半环.

定理2说明,半环S上的理想软半环在同态映射φ之下的原像集(φ-1(η),A)是半环R上的理想软半环.

例2取整数半环Z和模n(n∈Z+)剩余类半环Zn.对任意的x∈Z,令

φ:Z→Zn;x

由例1知,φ是从Z到Zn的一个同态映射.令A=Zn,且对任意的x∈A,令

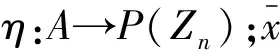
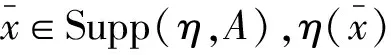
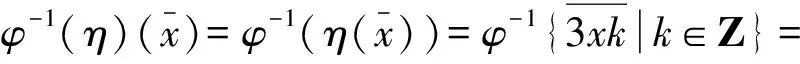
{3xk|k∈Z}=3xZ

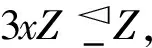
命题2设φ是从半环R到半环S的一个同态映射,(η,A)是S上的一个理想软半环.那么

1)若(η,A)是完全的,则(φ-1(η),A)是R上的一个完全理想软半环;

2)若R和S都是有零元半环,且(η,A)是平凡的,则当φ是单射,且0S∈φ(R)时,(φ-1(η),A)是R上的一个平凡理想软半环,其中0S是S的零元.

证明1)由定理2知,(φ-1(η),A)是R上的一个理想软半环.对任意的x∈A,由(η,A)是完全的得η(x)=S,于是有

φ-1(η)(x)=φ-1(η(x))=φ-1(S)=R

因此,(φ-1(η),A)是完全的.

2)由定理2知,(φ-1(η),A)是R上的一个理想软半环.由φ是单射,且0S∈φ(R)得φ-1(0S)=Kerφ={0R},其中0R是R的零元.对任意的x∈A,由(η,A)是平凡的得η(x)={0S},于是有

φ-1(η)(x)=φ-1(η(x))=φ-1{0S}={0R}

因此,(φ-1(η),A)是平凡的.

命题2说明,半环S上的平凡理想软半环(η,A)在单同态φ之下的原像集(φ-1(η),A)是半环R上的平凡理想软半环.

定义1设(η1,A)和(η2,B)都是半环R上的理想软半环,若

1)B⊆A;

则称(η2,B)是(η1,A)的一个理想软子半环.

例3取整数半环Z,令A=B=Z,且对任意的x∈A=B,令

η1:A→P(Z);x{2xk|k∈Z}

η2:B→P(Z);x{4xk|k∈Z}

则(η1,A)和(η2,B)都是Z上的理想软半环.

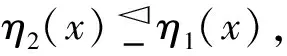
定义2设(η1,A)和(η2,B)都是半环R上的理想软半环,若(η1,A)和(η2,B)互为理想软子半环,则称(η1,A)和(η2,B)软相等.

定理3设φ是从半环R到半环S的一个满同态.那么

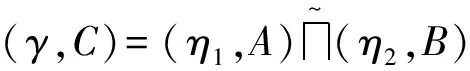
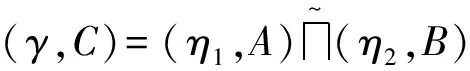
证明1)由定理1中(1)和文献[1]中定理4.6知,(φ(γ),C)和(ν,C)都是S上的理想软半环.对任意的x∈C=A∩B,有

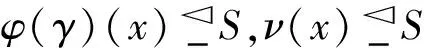
2)由定理2和文献[1]中定理4.6知,(φ-1(γ),C)和(δ,C)都是R上的理想软半环,于是由1)得(φ(δ),C)和(φ(φ-1(γ)),C)都是S的理想软半环.

对任意的x∈C=A∩B,有

由于φ是满射,因此,

φ(φ-1(γ)(x))=η1(x)∩η2(x),φ(δ(x))⊆

η1(x)∩η2(x)

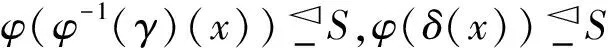
故(φ(δ),C)是(φ(φ-1(γ)),C)的理想软子半环.

定理4设φ是从半环R到半环S的一个满同态.那么

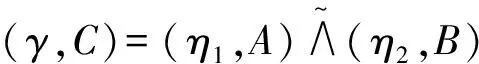
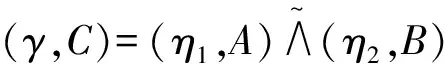
证明1)由定理1中1)和文献[1]中定理4.9知,(φ(γ),C)和(ν,C)都是S上的理想软半环.对任意的(x,y)∈C=A×B,有

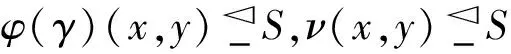
2)由定理2和文献[1]中定理4.9知,(φ-1(γ),C)和(δ,C)都是R上的理想软半环,于是由定理1中1)知,(φ(φ-1(γ)),C)和(φ(δ),C)都是S上的理想软半环.

对任意的(x,y)∈C=A×B,有

由φ是满射得

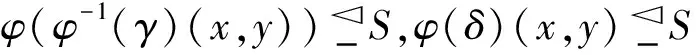
定理5设φ是从半环R到半环S的一个同态映射.那么

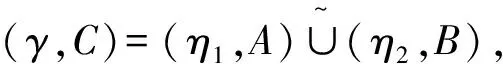
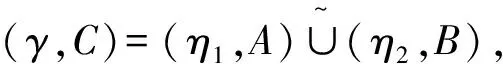
证明1)由定理1中1)和文献[1]中定理4.7知,(φ(γ),C)和(ν,C)都是S上的理想软半环.对任意的x∈C,由A∩B=∅知,

很显然,φ(γ)(x)和ν(x)相等,互为理想,故(φ(γ),C)和(ν,C)软相等.

2)由定理2和文献[1]中定理4.7知,(φ-1(γ),C)和(δ,C)都是R上的理想软半环.

对任意的x∈C,由A∩B=∅知,

很显然,φ-1(γ)(x)和δ(x)相等,互为理想,故(φ-1(γ),C)和(δ,C)软相等.

致谢：本文得到天水师范学院校级一般项目(JY203008)的资助，在此表示感谢.