关于半模同态的分解*

艾 鑫，黎奇升

(吉首大学数学与统计学院，湖南 吉首 416000)

半环作为常见的代数结构，不仅在拓扑学、分析学和最优化理论中有较广泛的应用，而且在计算机科学中有极其重要的应用.半模作为半环的一种表示，既是环模的推广，也是研究半环结构的有效方法，而半模同态分解在研究半模范畴性质中具有重要的作用.设M，N为左R-半模，f:M→N为半模同态.J.Al-Thani[1]利用核{a∈A|f(a)=0}和象{b∈B|b+f(a)=f(a′)}的定义对半模同态的分解问题进行了研究，并在k-投射半模中讨论了其可裂性.甘爱萍等[2]利用同余关系，对半模范畴中的第三同构定理进行了讨论，当f为k-正则半模同态时，同构定理成立.陈培慈[3]对半环理论及其应用进行了研究与整理，利用同余关系Kerf={(x，y)|f(x)=f(y)，x，y∈S}给出了半环同态的基本定理及其相关推论.笔者将从核与象的不同定义出发探讨左R-半模的同态分解问题，并给出半模同态分解定理.

1 相关定义

文中，半环R均指有单位元的结合半环，R-半模M均是左酉半模.关于半环、半模的定义和基本性质参见文献[3].设M，N为左R-半模，f:M→N为半模同态.令

Kf={m|f(m)=0}，Kerf={(m1，m2)|f(m1)=f(m2)，m1，m2∈M}，

If={f(m)|m∈M}，Imf={n∈N|n+f(m)=f(m′)，∃m，m′∈M}，

若Imf=If，则称f是i-正则的.若对于∀(m1，m2)∈Kerf，∃k1，k2∈Kf，使得m1+k1=m2+k2，则称f是k-正则的.不难看出:f是单同态当且仅当Kerf={(x，x)|x∈M};f是满同态当且仅当If=N;若f是单同态，则Kf={0}，反之则不真;若f是满同态，则Imf=N，反之不成立.

2 主要结果

定理1设M，M′，N，N′为左R-半模，f:M→N为同态.

(1)若g:M→M′是满同态，Kerg⊆Kerf，则存在唯一同态h:M′→N，使得f=hg，且Kerh=g(Kerf)，If=Ih，其中g(Kerf)={(g(x),g(y))|(x,y)∈Kerf},h是单同态当且仅当Kerf=Kerg，h是满同态当且仅当f是满同态.

(2)若g:N′→N是单同态，If⊆Ig，则存在唯一的同态h:M→N′，使得f=gh，且Kerh=Kerf，Ih=g-1(If)，h是单同态当且仅当f是单同态，h是满同态当且仅当If=Ig.

证明(1)对于∀m′∈M′，由于g:M→M′是满同态，因此必存在m1∈M，使得g(m1)=m′.若m2∈M，满足g(m2)=m′，则g(m1)=g(m2)，从而(m2，m1)∈Kerg，又由Kerg⊆Kerf，于是f(m1)=f(m2).这表明f(m1)与m1的选取无关.因此，存在一个函数h:M′→N，使得h(g(m))=f(m).下证f是半模同态.事实上，对于∀a，b∈R，m1′，m2′∈M′，∃m1，m2∈M，使得g(m1)=m1′，g(m2)=m2′.于是

h(am1′+bm2′)=h(g(am1)+g(bm2))=hg(am1+bm2)=f(am1+bm2)=

af(m1)+bf(m2)=ah(m1′)+bh(m2′)，

从而h为半模同态.若又有h′:M′→N，使得f=h′g，任取m′∈M′，∃m∈M，使得g(m)=m′，于是h′(m′)=h′g(m)=f(m)=hg(m)=h(m′)，即h=h′.

现证Kerh=g(Kerf).对于∀m1′，m2′∈g(Kerf)，∃(m1，m2)∈Kerf，使得g(m1)=m1′，g(m2)=m2′.因为f(m1)=f(m2)，f(m1)=hg(m1)=h(m1′)，f(m2)=hg(m2)=h(m2′)，所以(m1′，m2′)∈Kerh.反之，对于∀(m1′，m2′)∈Kerh，∃m1，m2∈M，使得g(m1)=m1′，g(m2)=m2′.因为h(m1′)=h(m2′)，h(m1′)=f(m1)，h(m2′)=f(m2)，所以(m1，m2)，(m2，m1)∈Kerf，于是(m1′，m2′)∈g(Kerf).综上可得Kerh=g(Kerf).

If=Ih显然成立，由此可知h是满同态当且仅当f是满同态.当h为单同态时，Kerh={(m′，m′)|m′∈M′}.对于∀(m1，m2)∈Kerf，有f(m1)=f(m2)，从而hg(m1)=hg(m2).因为h是单同态，所以g(m1)=g(m2)，于是(m1，m2)∈Kerg，从而Kerf⊆Kerg.又因为Kerg⊆Kerf，所以Kerg=Kerf.假设Kerf=Kerg.对于∀(m1′，m2′)∈Kerh，∃m1，m2∈M，使得g(m1)=m1′，g(m2)=m2′.因为h(m1′)=h(m2′)，f=gh，所以f(m1)=f(m2)，(m1，m2)∈Kerf=Kerg，于是g(m1)=g(m2)，m1′=m2′，这表明h是单同态.

(2)对于∀m∈M，有f(m)∈If⊆Ig，由于g单，从而存在唯一的n′∈N′，使得g(n′)=f(m).令h(m)=n′，由此定义一个函数h:M→N′满足f=gh.由f，g均为半模同态，不难验证h是半模同态.下证Kerh=Kerf.显然Kerh⊆ Kerf，只需证明Kerf⊆Kerh.任取(m1，m2)∈Kerf，有f(m1)=f(m2)，即gh(m1)=gh(m2).因为g是单同态，所以h(m1)=h(m2)，从而(m1，m2)∈Kerh.下证Ih=g-1(If).据h的定义，不难验证Ih⊆g-1(If).对于∀n′∈g-1(If)，∃m∈M，使得f(m)=g(n′)，由于g为单同态，根据h的定义有h(m)=n′，因此n′∈Ih，g-1(If)⊆Ih，于是Ih=g-1(If).因为Kerh=Kerf，所以无论h，f哪一个为单，都可以得到另一个同态为单.当h满同态时，有f(M)=g(h(M))=g(N′)，显然Ig=If.而当Ig=If时，意味着对于∀n′∈N′都有g(n′)⊆If，即∃m∈M，使得h(m)=n′.

推论1设R，S和R′是半环，f:R→S是半环同态.若g:R→R′是半环满同态，Kerg⊆Kerf，则存在唯一半环同态h:R′→S，使得f=hg，且Kerh=g(Kerf)，If=Ih，h是单同态当且仅当Kerf=Kerg，h是满同态当且仅当f是满同态.

推论2设M，N为左R-半模，f:M→N是半模同态，则存在唯一的单同态η:M/Kerf→N，使得ηυ=f，其中υ为M到商半模M/Kerf的自然同态.

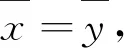
推论3设M，N为左R-半模.若f:M→N是满同态，则存在唯一的同构η:M/Kerf→N，使得ηυ=f，其中υ为M到商半模M/Kerf的自然同态.

推论4设M，N为左R-半模，f:M→N是半模同态，则η:M/Kerf≃If.

推论5设f:M→N为左R-半模M到N的同态，S是M上的同余关系.若S⊆Kerf，则存在同态h:M/S→N，使得f=hυ，其中υ为M到M/S的自然同态.

推论6设M，M′，N，N′为左R-半模，f:M→N为同态.

取核定义Kf={m|f(m)=0}，象定义If={f(n)|n∈N}时，有如下结论：

定理2设M，M′，N，N′为左R-半模，f:M→N为R-同态.

(1)若g:M→M′是k-正则满同态，Kg⊆Kf，则存在唯一同态h:M′→N，使得f=hg，且Kh=g(Kf)，If=Ih，h是单同态当且仅当Kf=Kg，h是满同态当且仅当f是满同态.

(2)若g:N′→N是单同态，If⊆Ig，则存在唯一的同态h:M→N′，使得f=gh，且Kh=Kf，Ih=g-1(If)，h是单同态当且仅当f是单同态，h是满同态当且仅当If=Ig.

证明(1)对于∀m′∈M′，∃m1∈M，使得g(m1)=m′.若m2∈M，满足g(m2)=m′，则g(m1)=g(m2).因为g是k-正则的，所以∃k1，k2∈Kg，使得m1+k1=m2+k2，于是f(m1+k1)=f(m2+k2).因为Kg⊆Kf，所以f(m1)=f(m2).这表明f(m1)与m1的选取无关.因此，存在函数h:M′→N，使得h(g(m))=f(m).不难证明h是半模同态.

任取m∈Kf，有f(m)=0，由f=hg，有h(g(m))=0，于是g(m)∈Kh，从而g(Kf)⊆Kh.任取m′∈Kh，因为g为满同态，所以∃m∈M，使得g(m)=m′.于是f(m)=hg(m)=h(m′)=0，从而m∈Kf，m′=g(m)∈g(Kf)，故Kh⊆g(Kf).综上可得Kh=g(Kf).由g为满同态，不难证明Ig=If.

若h为单同态，则有Kh={0}.注意到Kh=g(Kf)，有g(Kf)=0，从而Kf⊆Kg.据条件Kg⊆Kf，于是Kf=Kg.反之，假设Kf=Kg.对于∀(m1′，m2′)∈Kerh，∃m1，m2∈M，使得g(m1)=g(m2).因为h(m1′)=h(m2′)，所以h(g(m1))=h(g(m2))，即f(m1)=f(m2).又因f是k-正则的，故∃k1，k2∈Kf，满足m1+k1=m2+k2，于是g(m1)=g(m2)，即m1′=m2′.这证明了h是单同态.由Ih=If，不难看出h是满同态当且仅当f是满同态.

(2)对于∀m∈M，有f(m)∈If⊆Ig.由于g单，从而存在唯一的n′∈N′，使得g(n′)=f(m).令h(m)=n′，由此定义函数h:M→N′满足f=gh.由f，g均为半模同态，不难验证h是半模同态.下证Kh=Kf.显然Kh⊆Kf.对于∀m∈Kf，有g(h(m))=f(m)=0，因g是单同态，故h(m)=0，从而m∈Kh.据定理1可得Ih=g-1(If)，h是单同态当且仅当f是单同态，h是满同态当且仅当If=Ig.

推论7设R，S和S′是半环，f:R→S是k-正则的半环同态，若g:R→R′是满同态，Kg⊆Kf，则存在唯一半环同态h:R′→S，使得f=hg，且Kh=g(Kf)，If=Ih，h是单同态当且仅当Kf=Kg，h是满同态当且仅当f是满同态.

将R，R′，S视为左R-半模，利用定理2仿照推论1可类似证明推论7.

取核定义Kerf={(m1，m2)|f(m1)=f(m2)}，象定义Imf={n∈N|n+f(m)=f(m′)，m∈M}时，有如下结论：

定理3设M，M′，N，N′为左R-半模，f:M→N为R-同态.

(1)若g:M→M′是满同态，Kerg⊆Kerf，则存在唯一同态h:M′→N，使得f=hg，且Kerh=g(Kerf)，Imf=Imh，h是单同态当且仅当Kerf=Kerg，h是满同态当且仅当f是满同态.

(2)若g:N′→N是i-正则单同态，Imf⊆Img，则存在唯一的同态h:M→N′，使得f=gh，且Kerh=Kerf，Imh=g-1(Imf)，h是单同态当且仅当f是单同态，h是满同态当且仅当If=Ig.

证明(1)根据定理1，只需证明Imf=Imh.对于∀n∈Imh，∃m1′，m2′∈M′，使得n+h(m1′)=h(m2′).因g是满同态，故∃m1，m2∈M，使得g(m1)=m1′，g(m2)=m2′，于是n+h(g(m1))=h(g(m2))，即n+f(m1)=f(m2)，根据Imf的定义，有n∈Imf.反之，对于∀n∈Imf，∃m1，m2∈M，使得n+f(m2)=f(m2).由于f=hg，因此n+h(g(m1))=h(g(m2))，注意到g(m1)，g(m2)∈M′，必有n∈Imh.综上可得Imf=Imh.

(2)因g是i-正则的，故Img=Ig.显然If⊆Imf，于是If⊆Imf⊆Img=Ig.根据定理1，存在唯一的同态h:M→N′，使得f=gh，且Kerh=Kerf.下证Imh=g-1(Imf).对于∀n′∈Imh，∃m1，m2∈M，使得n′+h(m1)=h(m2)，于是g(n′+h(m1))=g(h(m2))，g(n′)+f(m1)=f(m2)，可得g(n′)∈Imf，n′∈g-1(Imf).反之，假设n′∈g-1(Imf)，则g(n′)∈Imf，于是∃m1，m2∈M，使得g(n′)+f(m1)=f(m2)，注意到f=gh，必有g(n′+h(m1))=g(h(m2)).因g是单同态，故n′+h(m1)=h(m2).根据Imh的定义，有n′∈Imh.