Schrödinger方程在Neumann边界控制下的正则性与能观测性

白忠玉

(海口经济学院 网络学院, 海南 海口 571127)

Schrödinger方程是经典发展方程,广泛出现在量子力学、等离子体物理和非线性光学等许多科学领域.关于其解的存在性和唯一性已被深入研究[1-4].虽然Schrödinger方程控制问题已有许多研究结果[5-8],但对一个具体给定的有实际背景的Schrödinger方程控制系统,判断其适定正则性和能控性并不容易.

Wen等[9]证明了带有Dirichlet边界控制的Schrödinger方程的适定性,而没有给出正则性的证明.本文的目的是研究Neumann边界控制和同位观测的Schrödinger方程(1)的正则性与能观测性.利用适定性结果,证明系统(1)是正则的；将文献[9]中研究Dirichlet边界能控性的方法推广到Neumann边界上,得出系统(1)的能观测性.

考虑如下Schrödinger方程：

(1)

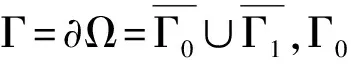
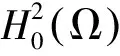
1 主要结果

下述定理表明系统(1)在状态空间H中,在输入和输出空间U=Y中是适定的[10],其证明与文献[9]中定理1类似,本文不再赘述.

定理1任给定常数T>0,存在仅依赖于T的常数CT>0,使得对任意初值w(·,0)=w0∈H,以及任意的输入u∈L2(0,T;U),系统(1)存在唯一的解w∈C(0,T;H),且

(2)

本文的第一个结果是正则性.

定理2系统(1)是正则的,并且其直接传输算子为零.确切地说,如果w(·,0)=wt(·,0)=0,且u(·,t)=u(·)∈U是一个阶跃输入,则相应的输出y满足:

(3)

本文的第二个结果是能观测性.

由定理1,下述系统(16)中的算子B是允许的,系统(1)的精确能控性等价于其对偶系统的精确能观测性[11].因此,考虑系统(1)的对偶系统：

(4)

定理3对任意T>0,系统(4)的解满足：

(5)

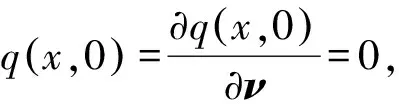
2 准备工作

先将系统(1)化为在状态空间H和输入输出空间U=Y中的一阶抽象系统.

令A是由如下的双线性形式a(·,·)在H中所确定的正定自共轭算子：

(6)

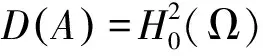
定义Dirichlet映射Υ∈L(L2(Γ0),H3/2(Ω)):Υu=v,其中v满足:

(7)

利用Dirichlet映射Υ,系统(1)可改写为

(8)

注意到D(A1/2)=L2(Ω)[15],A1/2是从L2(Ω)到H的等距同构[16].由于D(A)在H中稠密,从而D(A1/2)也在H中稠密.将空间H与其对偶H′等同,则下面的Gelfand三元对满足嵌入关系:

(9)

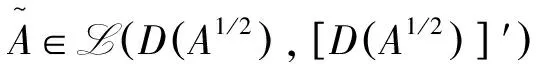
(10)

所以式(8)可以进一步在[D(A1/2)]′中改写为

(11)

其中B∈L(U,[D(A1/2)]′),由式(12)给定

(12)

定义B的共轭算子B*∈L(D(A1/2),U),即

〈B*f,u〉U=〈f,Bu〉D(A1/2),[D(A1/2)]′

∀f∈D(A1/2),u∈U

(13)

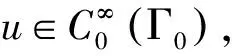
(14)

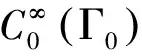
(15)

于是开环系统(1)可化为状态空间H中的一阶抽象系统：

(16)

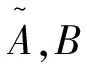
3 正则性

先证如下命题.

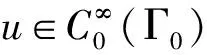
(17)

的解uε满足：

(18)

证明根据文献[14],系统(1)的传递函数为

(19)

只需证明在U的强拓扑下,H(λ)沿着正实轴趋向于零[17],即对于任意的u∈L2(Γ0)=U,有

(20)

此外,由文献[14],定理1宣称的适定性暗含着存在正常数M,α>0,使得

(21)

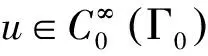
则wλ满足：

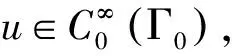
(24)

的唯一解.则方程(22)可化为

(25)

或

因此式(23)就成为

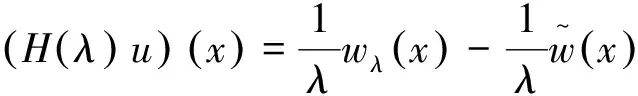
(26)

令uε(x)=wλ(x),即ε=λ-1,并取极限ε→0,则由式(26)知命题成立.证毕.

定理2的证明由命题1,只需证明式(18).

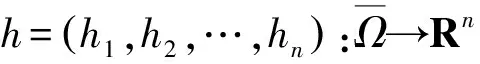
(27)

比较式(27)的实部,得

(28)

对式(27)的虚部采用同样的处理方法,得

(29)

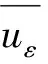
(30)

简单计算,有

(31)

其中Δh=(Δh1,Δh2,…,Δhn).

将式(31)代入式(30),得

(32)

又由椭圆正则性结果和Sobolev空间的迹定理[14],有下列不等式

(33)

这样,由式(32,33),得

(34)

其中Ci>0,i=1,2,3,4是不依赖于ε的常数.

最后,由文献[12],存在与ε无关的常数C5>0,方程(17)的解满足：

(35)

式(34)结合式(35),得

(C1+C2+C3)×

(36)

4 能观测性

考虑

(37)

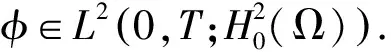
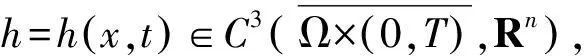
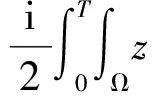
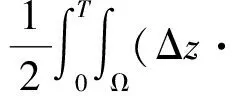
(38)

其中H(·)是Hessian矩阵.

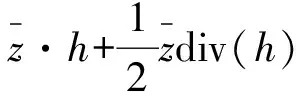
(39)

考虑边界条件,得

此外,

(42)

结合式(40～42),得

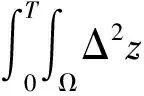
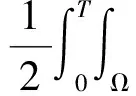
(43)

由式(39,43),得

(44)

对式(45～47)关于x分部积分,得

i,j=1,2,…,n

于是,∀x∈Γ,得

因此,

(48)

将式(45～48)代入式(44),结合式(37),得式(38).证毕.

定理3的证明取式(38)实部,令φ=0,得

对∀t∈[0,T],由Schrödinger方程的经典结果[19],系统(4)的解满足：

(49)

选取h(x,t)=x-x0,由式(38,49),得

进一步,∃ε>0,使得

因此,

(50)

为推出式(5),还要证明下列估计:

由Poincaré不等式直接可得式(51),下面证式(52).

假设式(52)不成立,则∀C>0,∃[0,T]上系统(4)的解序列{φn},满足：

(53)

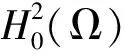
(54)

另一方面,式(53)暗含Δφ=0,(x,t)∈Γ×(0,T),结合系统(4)并由Holmgren唯一性定理[21]表明φ≡0.这与式(54)矛盾,从而式(52)成立.

由式(50～52),即得式(5).证毕.