事件触发脉冲控制下二阶多智能体系统的领导跟随一致性

金琬丽, 于志永, 蒋海军

(新疆大学 数学与系统科学学院, 新疆 乌鲁木齐 830017)

自1970年以来,作为协同控制的一个重要研究方向,多智能体一致性问题受到国内外研究者的密切关注.一致性是指由多个智能体通过相互作用最终行为上达到一致,通俗来讲就是指几个物体的状态通过外界控制或者自身内部的调整最终达到相同.在实际应用中,这个状态可以是速度、位置等.多智能体一致性控制问题具有丰富的实际背景和重要的实际应用价值,比如机器人协同控制[1],飞机编队飞行[2],智能电网等.多智能体系统一致性问题的发展最早追溯到1962年,Degroot[3]将一致性思想应用到多传感器的研究中.直到2004年,Olfati-Saber[4]提出了一致性的准确定义并建立了一致性研究的基本框架.

然而，早期主要集中研究连续控制下的多智能体一致性[5-6].由于带有微型处理器的智能体处理信息能力有限,连续控制不能应用于复杂的控制环境.考虑到脉冲控制只需在固定的时间点输入信息,这样就可以节约资源并有效弥补连续控制的不足,故采用脉冲控制下研究智能体系统的一致性更加符合实际需求.因此,脉冲控制策略被广泛应用于多智能体系统的协同控制问题[7-11].针对无领导者和有领导者的两种情况，Can等[7]提出了部分状态约束脉冲和完全状态约束脉冲这两种不同的脉冲协议.再基于代数图论的李雅普诺夫稳定性理论,矩阵理论得到一些充分条件用于处理非线性多智能体系统的一致性.考虑到网络通讯拓扑并不是一直不变的,Yang等[8]基于代数图论和脉冲稳定性理论,利用脉冲控制研究了固定拓扑和切换拓扑下二阶多智能体系统一致性问题.对比文献[7,8]的脉冲是控制全部智能体,Guo等[9]提出了自适应脉冲牵制控制方法来控制部分智能体,再根据网络拓扑是否强连通,给出了两种控制协议解决了具有不确定扰动的多智能体系统的一致性问题.考虑到之前的收敛都是渐近收敛的,Xu等[10]提出了一种固定时间脉冲控制策略.利用Lyapunov函数,比较原理和平均脉冲间隔,证明系统最终在固定时间内达到一致性.此外,针对离散多智能体系统，Li等[11]通过考虑低增益反馈控制，提出了新的分布式脉冲控制策略,利用李亚普诺夫函数和低增益理论获得了一些条件,最终实现了系统的半全局一致性.上述这些控制协议主要利用脉冲控制方法研究多智能体系统一致性,但这一方法存在一个弊端就是需要提前设定好时间,为了操作简单,通常选取脉冲控制的时间都是周期的.

在实际应用中,周期采样控制会导致不必要的浪费.在网络通信中,如果能够减少智能体之间的通讯交流,就可以有效地解决网络带宽的拥挤问题.因此,事件触发采样控制策略应运而生.事件触发控制的原理是当智能体间状态误差超过了预先规定的阈值,执行器才会更新状态输入,否则保持不变,更新状态的时刻是预先未知的.目前,基于事件触发采样控制的多智能体一致性研究取得了很多成果,比如事件触发采样控制[12-15],量化事件触发采样控制[16-19].在文献[12-14]中,针对一阶，二阶和高阶多智能体系统,在事件触发采样控制协议下推导出合适的充分必要条件,排除Zeno行为的同时也实现了一致性.Han等[15]在事件触发采样控制下,研究了具有时变控制增益的非线性多智能体同步问题.为了实现同步,提出了更具灵活性的状态相关和时间相关的事件触发协议,利用含时参数的时滞微分不等式和李雅普诺夫函数最终证明了所提协议的有效性.当出现网络带宽和数据丢失情况时，为了减少网络通讯负担和克服网络约束，文献[16-20]将量化和事件触发控制结合起来解决这一类问题.Wu等[16]讨论了带有均一量化器的牵制事件触发控制策略,利用非光滑分析和Gronwall不等式方法保证闭环系统解的存在性,通过量化事件触发可以达到多智能体系统实际的一致性，并收敛到一个一致性集.为了处理不匹配的外部干扰的存在，Yuan等[17]提出了一种新的多面不连续滑模面，通过考虑构造滑模控制律，结合事件触发机制和动态量化机制.在此方案下，证明了所有的状态轨迹最终达到一致，而Wu等[18]则利用带有均一量化的高增益控制协议结合事件触发控制方法获得了多智能体系统的有界一致性，Ma等[19]则将量化改进为动态量化和事件触发结合.这一方法有效解决了在智能体个数数量很多时，量化器的量化数量不会很大的问题，同时保证了多智能体系统达到了理想的一致性.Lian等[20]结合事件触发采样控制和量化滑模面设计方法,提出了两种不同类型的滑模控制策略.基于滑模控制原理,消除了干扰并且证明了不确定切换系统的一致性.

针对传统的一阶多智能体系统,Tan等[21]研究了事件触发脉冲控制下多智能体系统的领导跟随一致性,并排除了Zeno行为.然而一阶系统只能智能体描述系统的一部分信息,在现实生活中,很多智能体都应用二阶动力学模型来描述智能体的位置和速度信息,比如扭矩电机和气体射流,需要通过加速度来调整所需的运动.因此考虑二阶多智能体系统的一致性更具有挑战性和实际意义.许多学者也开始研究二阶系统,比如Zhang等[22]将二阶连续系统的编队问题转化成了多智能体一致性问题.在没有生成树和具有生成树的时变网络拓扑下,Gao等[23]采用了两种采样控制方法去设计控制增益和采样时刻使得系统达到一致.Duan等[24]设计了一种新的带速度测量和不带速度测量的分布式事件触发控制协议来确保二阶系统的追踪一致性行为,这一方法的缺点是需要持续控制.考虑到脉冲控制只需要脉冲瞬间工作的优点,本文结合脉冲采用事件触发脉冲控制方法研究二阶多智能体系统的领导跟随一致性问题.

基于此,本文运用Lyapunov稳定性理论和不等式放缩技巧,研究了在事件触发脉冲控制下具有领导者的二阶多智能体的一致性问题.与连续控制协议相比,本文提出的事件触发机脉冲制协议可以减少智能体之间的通讯,从而节省有限的资源.

本文中的记号：Rn代表n维列向量,R+表示正实数集,IN是指N维的单位矩阵.对于任意一个矩阵A,AT,λmin(A),λmax(A)分别代表了矩阵A的转置矩阵,最小和最大特征值.对于任意一个对称矩阵B,矩阵B>0(B<0)表示矩阵B是个正定(负定)矩阵.二范数用‖·‖定义.

1 预备知识及问题描述

1.1 代数图论

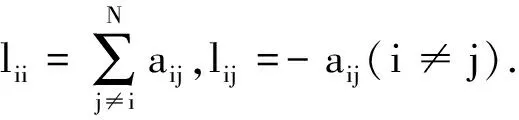
定义1如果无向图G的任意两个节点之间都有路径则称G是无向连通的.

引理1[23]如果L是无向连通图G的Laplacian矩阵,则L是具有N个实特征值的对称矩阵,且满足0=λ1<λ2<…<λN.此外,特征值0的特征向量为1N,即L1N=0.

假设1 跟随者之间的通讯拓扑图G是固定无向的.

1.2 问题描述

考虑具有领导者的二阶多智能体系统,其中领导者的动力学行为描述为

(1)

式中:x0(t)∈Rn,x0(t)∈Rn分别代表领导者在t时刻的位置、速度;A是具有合适维数的矩阵.

第i个跟随者的动力学描述为

(2)

式中:xi(t)∈Rn,vi(t)∈Rn,ui(t)∈Rn分别代表第i个智能体的位置、速度和控制输入.

定义2对于二阶多智能体系统(1,2)的任意初值,如果有

则称多智能体系统(1,2)达到领导跟随一致性.

设计如下事件触发脉冲控制协议

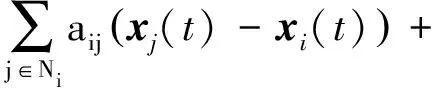
bi(x0(t)-xi(t))+

bi(v0(t)-vi(t))i=1,2,…,N

(3)

(4)

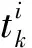
由Dirichlet函数性质,多智能体系统(1,2)在控制协议(4)下可以改写为

(5)

(6)

式中:fi(t)是需要设计的触发函数.由协议(4)可知,控制器只有在事件触发时刻对智能体进行脉冲控制,其余时间对系统不发生控制.因此,可以减少系统采样信息的频率.

事件触发函数被定义为

(7)

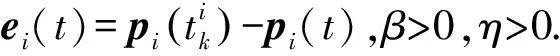
(8)

注1不同于一般的事件触发采样控制策略,本文提出的协议中,控制输入没有持续给出.只有系统状态符合触发条件时,控制器才会工作,其余时间控制器就会进入“休眠”状态,不进行脉冲控制.这有效减少了信息交换次数,可以避免网络拥堵的风险.

在分析中,将所有智能体的触发时刻依次从小到大排序写成事件触发矩阵σ(k),由于智能体的触发条件不同,每个智能体的触发时刻可能不同.在任意触发时刻,最少有一个,最多有N个事件被触发.当σi(k)=1时,代表第i个智能体在tk时刻被控制,否则,σi(k)=0.矩阵σ(k)代表不同智能体在不同时刻的控制分情况.由式(5)和式(8)可得

(9)

将式(9)改写为向量形式

(10)

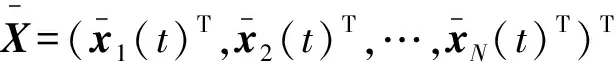
e(t)=(e1(t)T,e2(t)T,…,eN(t)T)T

矩阵σ(k)定义为

注2由于每个智能体的触发时刻依赖其触发条件,因此,不同智能体之间的触发时刻可能不同.在本文分析中,由于每个智能体的事件触发时刻不同,有可能导致触发时刻重叠.将所有触发时刻按照时间顺序排序后引入了矩阵σ(k).如果第一个智能体和第三个智能体在tk时刻被触发,σ(k)=[1N,0N,1N,…,0N].如果有i(1≤i≤N)个智能体在tk时刻被触发,则σ(k)=[1N,0N,…,1N,…,0N](1N的数量为i个).随着触发时刻的变化,1N和0N的位置在不断变化.利用这种方法,可以简化向量运算.

2 主要结果

为了使二阶多智能体系统(1,2)在事件触发脉冲控制协议(4)下实现领导跟随一致性问题,本文给出了如下定理.

2.1 一致性分析

定理1若假设1和假设2成立,在事件触发控制协议(4)下,如果存在实数域上的连续函数φ(t,t0),正常数α,β1,μ以及正定矩阵P1∈Rn×n使得下列条件成立

(11)

则二阶多智能体系统(1,2)可以达到领导跟随一致性,其中P、M、R、Q分别定义为

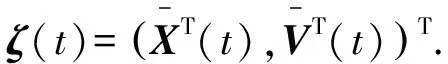
Vk(ζ)=V(ζ,k)=ζ(t)TPζ(t),k∈N+

(12)

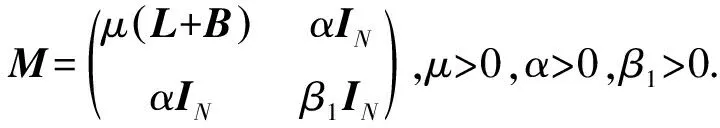
通过计算

结合式(10)和式(12),对Vk(ζ)求导可得

(13)

其中

由式(13)可知：

对上式积分可得

根据Gronwall不等式,当t∈(tk,tk+1]时,解得

(14)

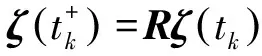
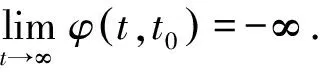
所以,在事件触发脉冲控制(4)下,二阶多智能体系统(1,2)可以达到领导跟随一致.

2.2 避免Zeno行为的证明

要排除Zeno行为,必须保证在有限时间内不会发生无限次触发.即要保证任意两次触发时间间隔大于正常数即可.

定理2若定理1的条件都成立,则在事件触发脉冲控制策略(4)下,二阶主从多智能体系统(1)和系统(2)不存在Zeno行为.

证明令

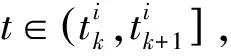
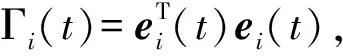
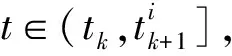
因此,

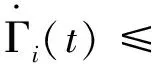
Γi(t)+ζTUζ

其中

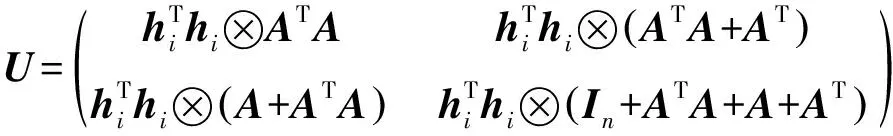
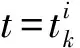
由事件触发函数(7)可知:

(15)

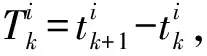
非空.因此,Zeno行为可以避免.

3 数值模拟

给出一个例子验证事件触发脉冲控制协议(4)的有效性.

例1考虑事件触发脉冲控制协议(4)下具有领导者的二阶多智能体系统(1,2),其中网络拓扑结构如图1所示,0代表领导者,其余的代表追随者.Laplacian矩阵L,对角矩阵B以及控制输入矩阵A分别为

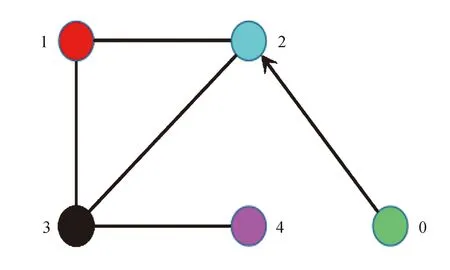
图1 网络拓扑

在数值仿真中,令γ=2,η=0.5,β=0.2.系统的初值为

X0(0)=(4,2.5,3)T

V0(0)=(0.2,-1,-0.3)T

X1(0)=(1,-2,0.1)T

V0(0)=(0.5,2,1.1)T

X2(0)=(-1.4,-1.8,2)T

V2(0)=(-3,1.8,-2)T

X3(0)=(5,1,-1.8)T

V3(0)=(3,2,1.8)T

X4(0)=(5,5,-2)T

V4(0)=(5,3.8,2.4)T

给定α=0.2,β1=0.2,μ=2,利用MATLAB解得矩阵

将矩阵P1带入满足定理1中的式(11).在图2～图4中绘制了多智能体i(i=0,1,2,3,4)的位置的运动轨迹.很容易看出,领导者和跟随者的状态最终趋于一致.每个智能体的事件触发时刻如图5～图8所示.可以看出,由于初始时刻智能体之间的状态误差比较大,所以智能体之间的触发频繁.在接近t=30 s触时,触发次数减少,到达一致后就不再触发,这说明事件触发脉冲控制可以有效地解决有限带宽的问题.

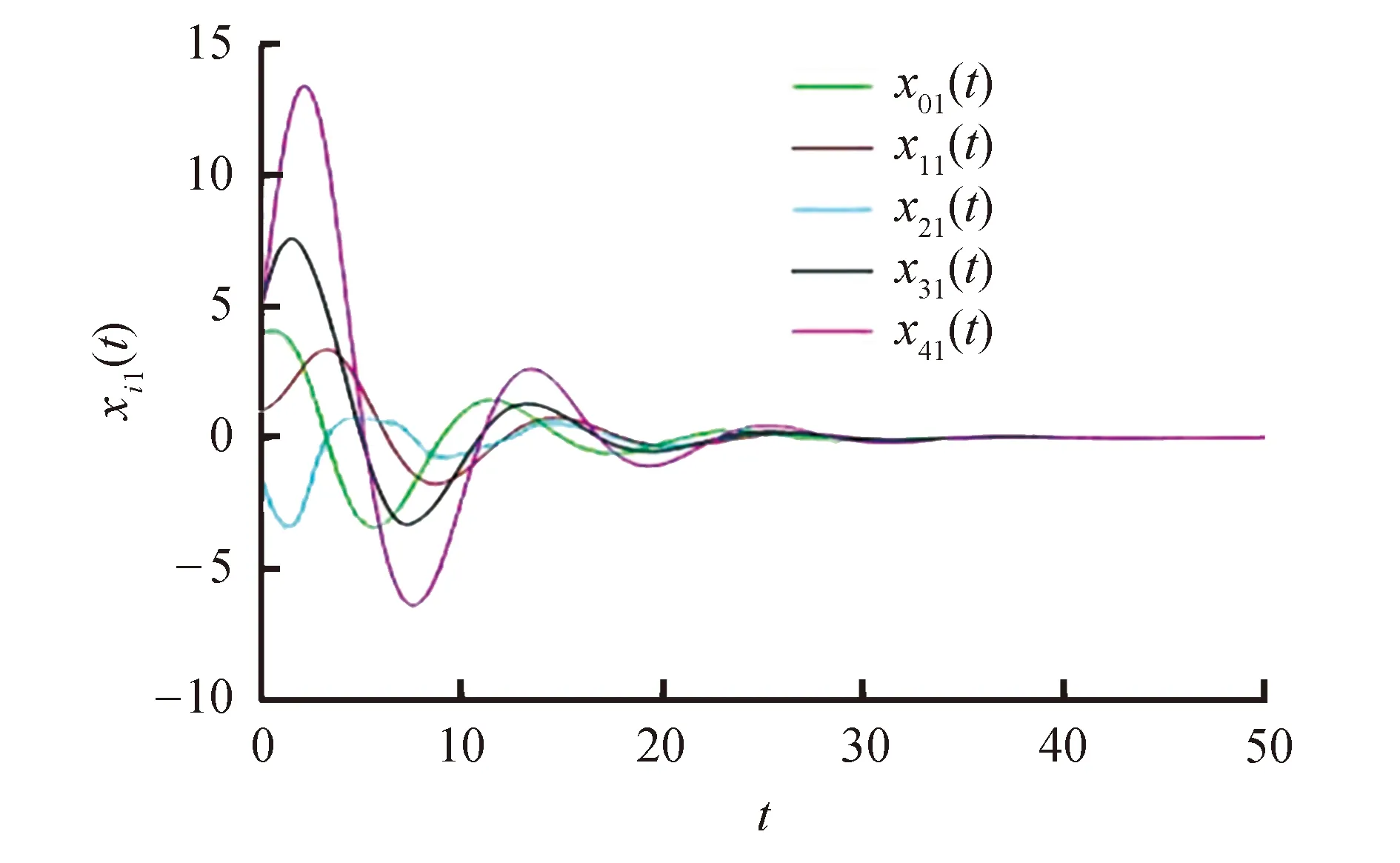
图2 智能体i的第1个分量的状态

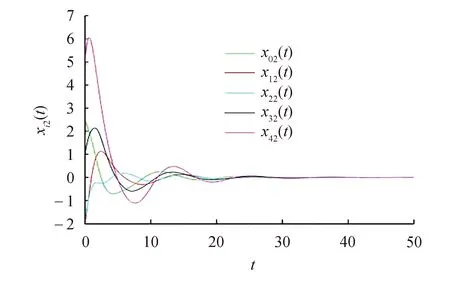
图3 智能体i的第2个分量的状态

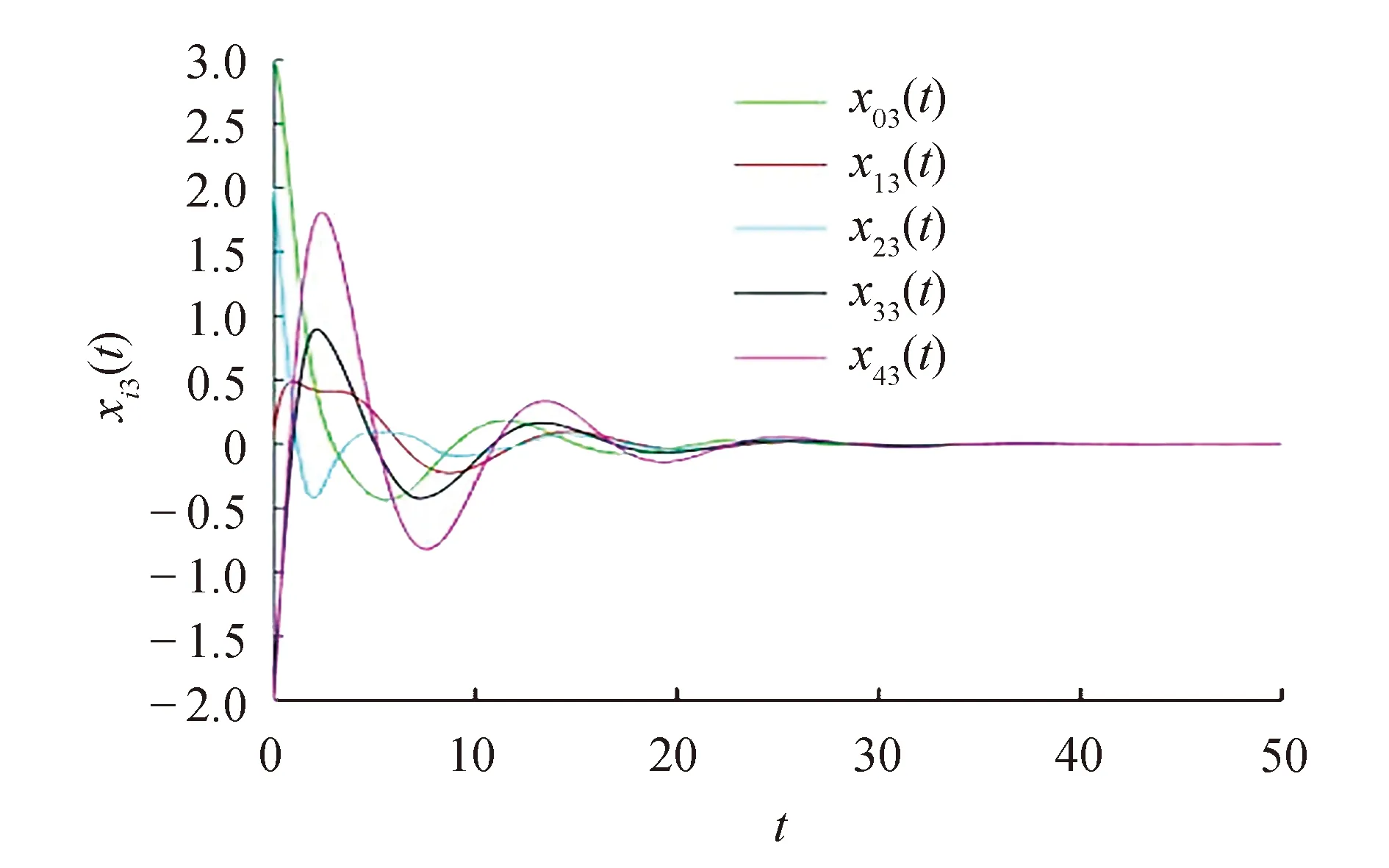
图4 智能体i的第3个分量的状态

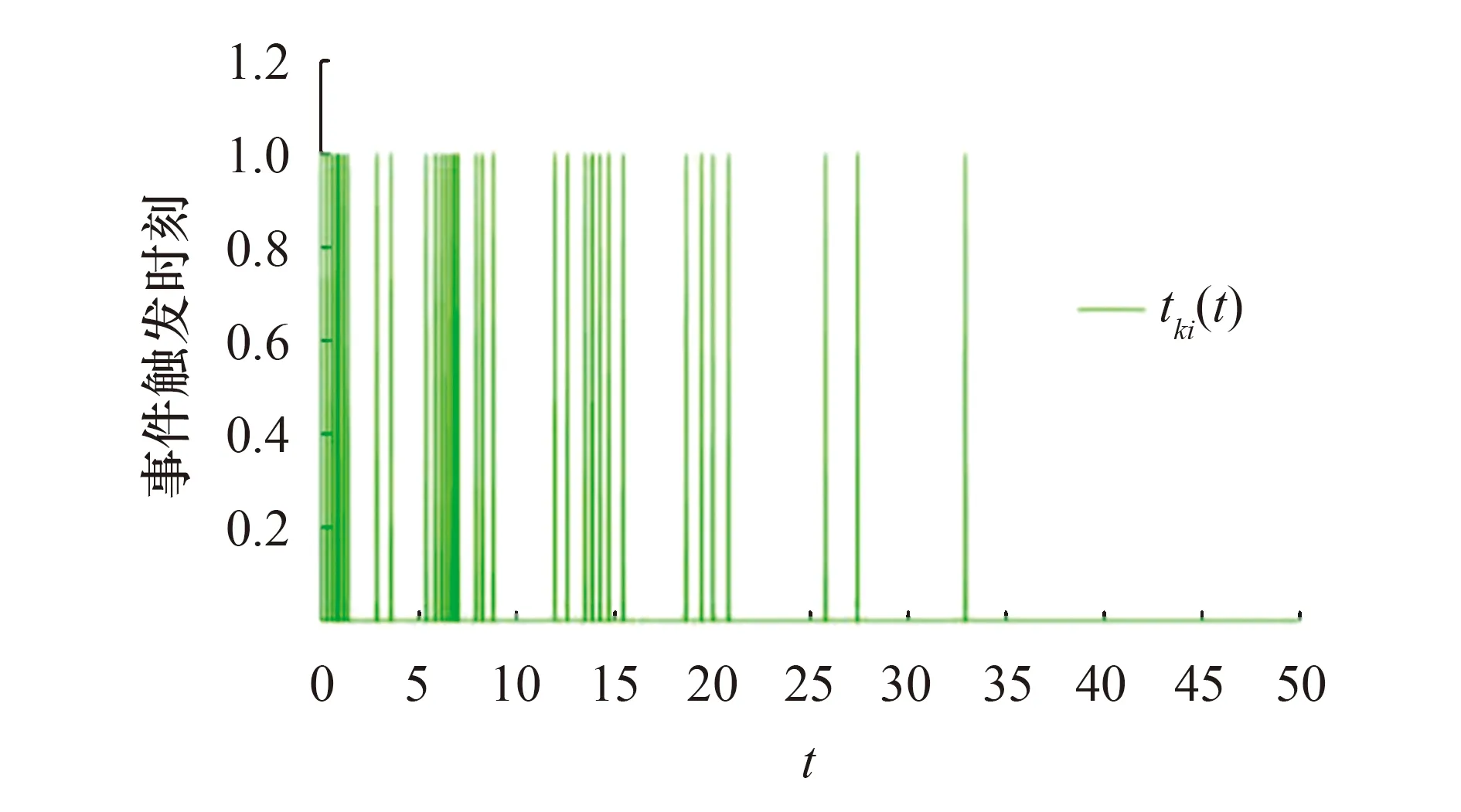
图5 第1个智能体的触发时刻

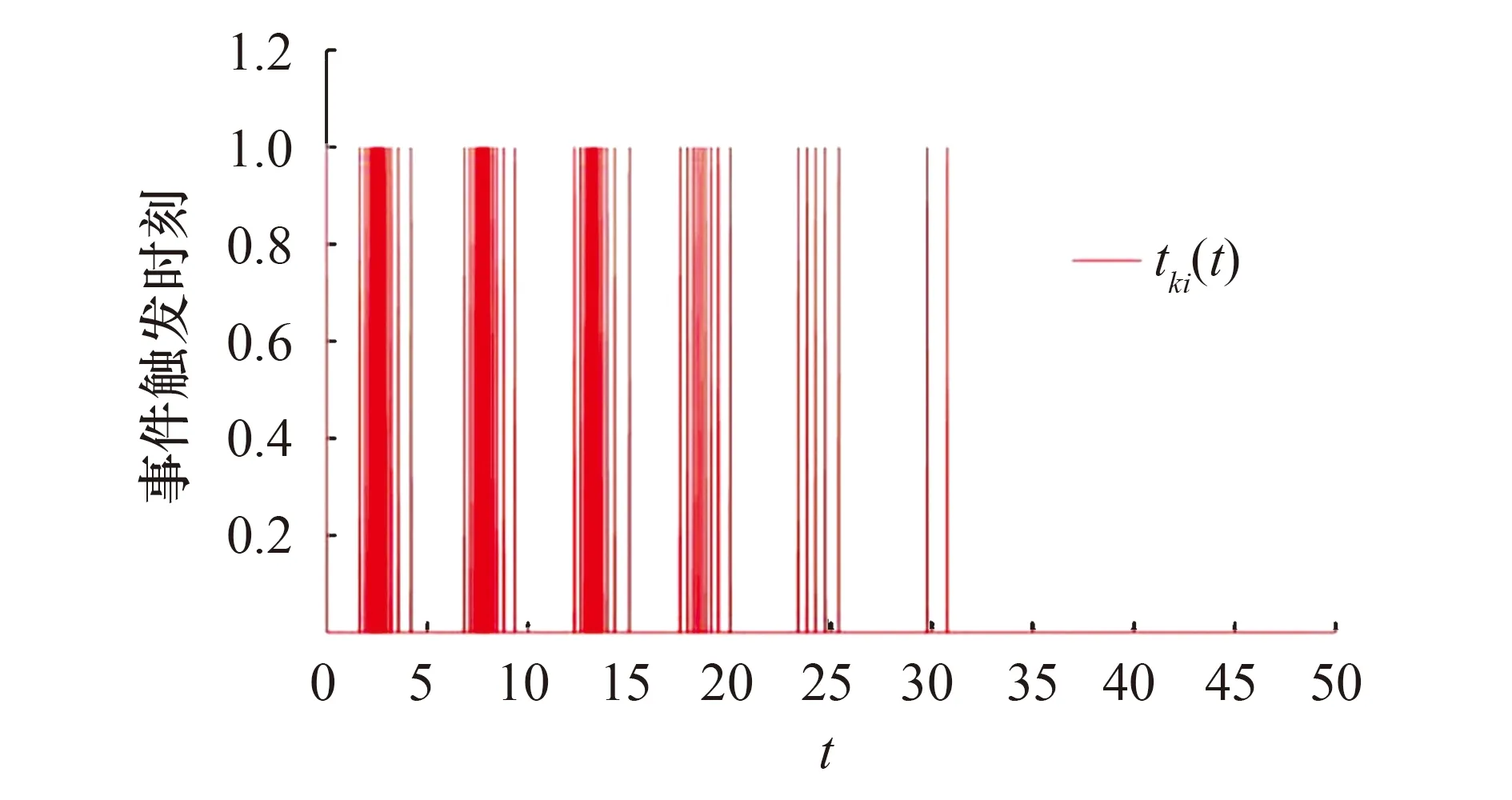
图6 第2个智能体的触发时刻

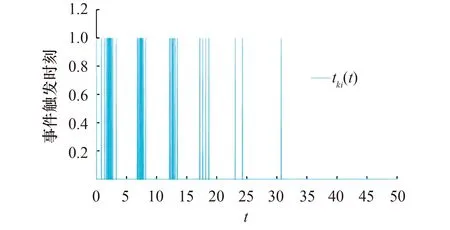
图7 第3个智能体的触发时刻

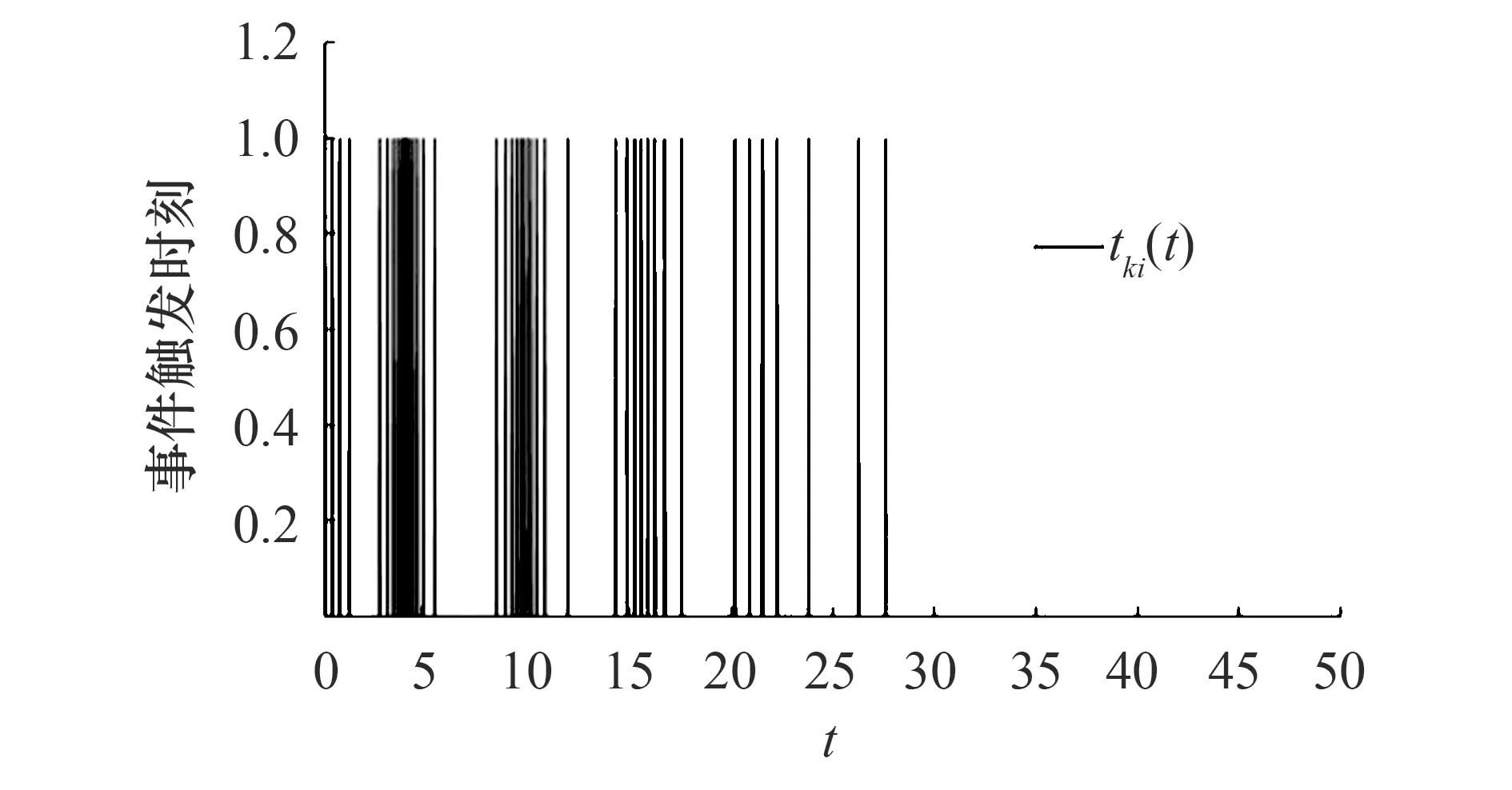
图8 第4个智能体的触发时刻

4 结论

本文通过提出一种新的事件触发脉冲控制策略,研究了二阶多智能体系统的领导跟随一致性.基于Lyapunov稳定性理论和矩阵图论以及不等式技巧,得到多智能体系统实现一致性的相关条件并排除了Zeno行为.利用数值仿真验证了控制协议的可行性.