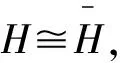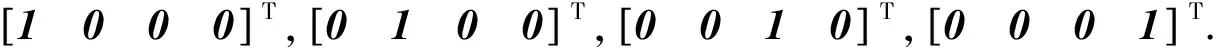图的广义距离特征值
2022-11-07卢鹏丽
卢鹏丽, 钟 雨
(兰州理工大学 计算机与通信学院, 甘肃 兰州 730050)
本文考虑简单连通图,设图G=(V(G),E(G))为含有n个顶点的简单连通图,其中V(G)={v1,v2,…,vn}表示点集合,E(G)为边集合.NG(vi)表示顶点vi∈V(G)的邻居集.顶点vi,vj∈V(G)之间的距离表示为dij(或dvi,vj),则距离矩阵可表示为D(G)=(dij)n×n,其特征值记为μ1≥μ2≥…≥μn.
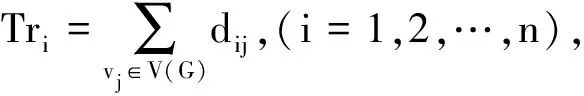

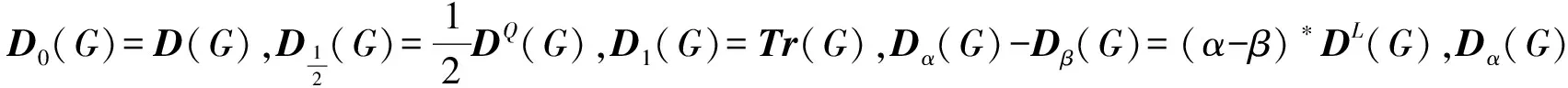
目前,关于广义距离矩阵的研究受到了广泛关注[10-15],Roberto[12]得出了图G经过加边运算后,它的广义距离谱半径会变小这一很实用的性质,研究了广义距离谱半径和距离拉普拉斯谱半径以及距离谱半径之间的一些不等关系等.Abdollah[13]等研究了广义距离矩阵第二大特征值的一些上下界,并验证了星图的第二大广义距离特征值是所有树中最小的.本文利用最大传递度Trmax、最小传递度Trmin、距离谱半径μ1等图参数得到了ρ1的一些上下界,并给出了极值情况;研究了ρ2关于阶数n和直径d的一个下界;计算了自补图的广义距离谱.
1 主要引理
引理1[16]若矩阵A是一个n×n的对称矩阵,并且其特征值为λ1≥λ2≥…≥λn,则对于所有的x∈Rn(x≠0),有λnxTx≤xTAx≤λ1xTAx.左式成立当且仅当x是A的特征值λn对应的特征向量,右式成立当且仅当x是A的特征值λ1对应的特征向量.

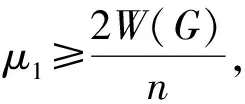
引理4[19]设A是一个n阶实对称矩阵,让其特征值λ1(A)≥λ2(A)≥…≥λn(A).若存在两个实对称矩阵N1和N2,使N=N1+N2,则λi(N1)+λ1(N2)≥λi(N)≥λi(N1)+λn(N2),i=1,2,…,n.
2 图的广义距离谱半径
给出n阶连通图G的广义距离谱半径的一些界.
定义Hn-1,δ为一个最大度为n-1,第二大度为Δ2,并且Δ2=δ(δ为图H的最小度)的连通图.特别的,Hn-1,n-1=Kn.
定理1设图G为n阶连通图,则
其中:B=αTri+Trj-(1-α)dij,等式成立当且仅当G≅Hn-1,δ或G是一个传递正则图.
证明设x=(x1,x2,…,xn)T为Dα(G)的特征值ρ1对应的特征向量,则
Dα(G)x=ρ1x
(1)
从式(1)的第k项,有
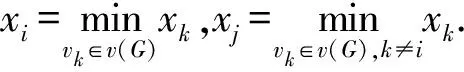
对于vi∈V(G), 由式(1)可得
因此
ρ1xi≥αTrixi+(1-α)Trixj
(2)
同理可得
因此
ρ1xj≥αTrjxj+(1-α)[dijxi+(Trj-dij)xj]
(3)
由式(2)和式(3),可得
(ρ1-αTri)(ρ1-Trj+(1-α)dij)≥(1-α)2dijTri
因此
所以
若定理1等号成立,则式(2)和式(3)中的等号一定成立,即∀vk∈V(G),k≠j,xk=xj恒成立.
考虑以下两种情况:
1)di=n-1.∀vj,vk∈NG(vi)(j≠k),可得
因为xj>0,并且xk=xj,所以由上式可得Trj=Trk,即G≅Hn-1,δ.
2)di 若xi=xj=xk,则有 ρ1xi=Tr1xi=Tr2xi=…=Trnxi 所以Tr1=Tr2=…=Trn,即G是一个传递正则图. 若xi 因此,Trk=Trl,因为di ρ1xj=(Trp-2(1-α))xj+2(1-α)xi 因为dip=2,所以∃vk∈V(G),使得vi,vp∈NG(vk),对于vi,vp∈NG(vk),可得 (Trp-2(1-α))xj+2(1-α)xi= (Trk-(1-α))xj+(1-α)xi 移项化简可得 (1-α)xi=(Trk-Trp+(1-α))xj 因为xi,xj均为正数,若Trk≥Trp,则有xi≥xj,与xi (1-α)xi=(Trk-Trp+(1-α))xj≤-αxj≤0 与xi>0矛盾.该定理得证. 定理2设图G为n阶连通图,则 αTrmin+(1-α)μ1≤ρ1≤αTrmax+(1-α)μ1 其中Trmin≤Tri≤Trmax(1≤i≤n).等式成立当且仅当G是一个传递正则图. 证明设x=(x1,x2,…,xn)T为Dα(G)的特征值ρ1对应的单位特征向量,则 因为 (4) ρ1≤αTrmax+(1-α)μ1 设y=(y1,y2,…,yn)T为D(G)的特征值μ1对应的单位特征向量,则 由引理1可知: 再次由引理1可得 定理2右边等式成立当且仅当x既是Dα(G)的特征值ρ1对应的单位特征向量,又是D(G)的特征值μ1对应的单位特征向量,即 因为xi≥0,所以ρ1=αTri+(1-α)μ1,(1≤i≤n),因此Tr1=Tr2=…=Trn. 同理可得,定理2左边等式成立当且仅当Tr1=Tr2=…=Trn.该定理得证. 推论1设图G为n阶连通图,则 其中Λ=αTrmax+(1-α)μ1,等式成立当且仅当G是传递正则图. 证明由引理2可知:Trmin≤μ1≤Trmax,再结合引理3和定理2得证. 给出了图的第二大广义距离特征值的一个基于阶数n和直径d的下界. 定理3设图G为一个直径为d的n阶连通图,则 其中Ψ=4(1-α)2(d-1)2. 证明设Pd+1:v1v2…vd+1为图G中一条直径路.设Θ={vi∈V(G)V(Pd+1)|dv1,vi+dvi,vd+1=d},|Θ|=θ,则0≤θ≤n-d-1. 因为dv1,vk+dvd+1,vk≥d,d+2≤k≤n,所以 由引理4可知: ρ2(G)≥λ2(Dα(G)-Dα(Kn))+ρn(Kn)≥ λ2(B)+ρn(Kn) 所以 因为 是一个关于x的减函数,所以f(x)≥f(n-d-1).又因为ρn(Kn)=αn-1,所以 该定理得证. 定理4设图G为n阶r-正则图,其邻接矩阵A的谱为{r,λ2,…,λn}.则自补图H的广义距离谱为 1)α(8n-2-r)-(1-α)(2+λi),i=2,3,…n,每一个重数为2; 2)α(5n-1+r)+(1-α)(λi-1),i=2,3,…,n,每一个重数为2; 其中 证明由自补图的定义可知H的广义距离矩阵Dα(H)可表示为 其中:M*=α(8n-2-r)I+(1-α)(2J-2I-A);N*=α(5n-1+r)I+(1-α)(J-I+A);J为全一矩阵;I为单位矩阵. 因为G是r-正则图,所以A的特征值r所对应的特征向量是全一向量1,其余特征向量都与1正交.设A的特征值λi(i=2,3,…,n)所对应的特征向量为Xi,则AXi=λiXi,1TXi=0. 设ν是矩阵Dα(H)的特征向量ψ对应的特征值,根据Dα(H)ψ=νψ和A1=r1可得 Μ1a+(1-α)nb+2(1-α)nc+3(1-α)nd=νa (1-α)na+Μ2b+(1-α)nc+2(1-α)nd=νb 2(1-α)na+(1-α)nb+Μ2c+(1-α)nd=νc 3(1-α)na+2(1-α)nb+(1-α)nc+Μ1d=νd 其中: Μ1=α(8n-2-r)+(1-α)(2n-2-r) Μ2=α(5n-1+r)+(1-α)(n-1+r) 假设a=0,带入上面方程组,化简得b=c=d=0,矛盾.因此,不失一般性,假设a=1,求解上面的方程组可得定理中的第(3)和第(4)部分,该定理得证. 推论2设图G为n阶r-正则图,其邻接矩阵A的谱为{r,λ2,…,λn}.则自补图H的距离拉普拉斯谱为 1)8n-r+λi,i=2,3,…,n,每一个重数为2; 2)5n+r-λi,i=2,3,…,n,每一个重数为2; 证明已知Dα(H)-Dβ(H)=(α-β)DL(H),取α=1,β=0,得DL(H)=D1(H)-D0(H),则由定理4可得推论2. 推论3设图G为n阶r-正则图,其邻接矩阵A的谱为{r,λ2,…,λn}.则自补图H的距离无符号拉普拉斯谱为 1)8n-4-r-λi,i=2,3,…,n,每一个重数为2; 2)5n-2+r+λi,i=2,3,…,n,每一个重数为2;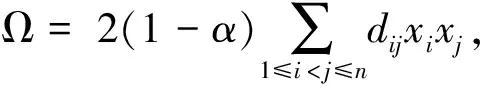
3 图的第二大广义距离特征值
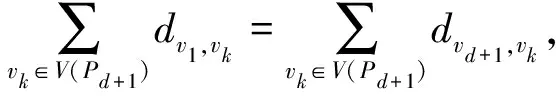
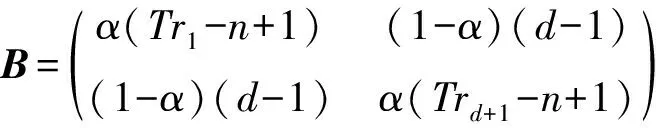
4 自补图的广义距离谱