对合K-正则半环

冯军庆， 徐　慧

(空军工程大学 理学院， 陕西 西安 710051)



对合K-正则半环

冯军庆*， 徐慧

(空军工程大学 理学院， 陕西 西安 710051)

研究对合K-正则半环的性质，利用K-正则半环的Green-关系从多个角度刻画对合K-正则半环，对合半群的幂半环是对合K-正则半环当且仅当对合半群是对合正则半群，最后给出对合正则半群的幂半环是对合交换半环的几个等价命题。

对合K-正则半环；K-幂等元； 幂等元半环； 幂半环

MR subject classification: 19A49

1　预备知识

若非空集合S上装有两个二元运算加法(+)和乘法(·)，其中(S,+)和(S,·)是半群，且满足乘法对加法的分配律，即

∀a、b∈S,a(b+c)=ab+ac,

则称(S,+,·)是半环。以下在不引起混淆的情况下，半环(S,+,·)简写为S。

含对合*运算的半环(S,+,·,*)[1]是指(S,+,·)是半环，且有下式成立：

∀x、y∈S, (x+y)*=y*+x*,

(xy)*=y*x*, (x*)*=x。

*是S上的反自同构，*也可以看作半环上的一元运算，把含对合*运算的半环简称为对合半环[1]。

半环(S,+,·)称为K-正则半环[2]是指(S,+)是半格，且对任意a∈S，都存在x∈S，使得a+axa=axa。本文中把含对合*运算的K-正则半环称为对合K-正则半环。

对合半环在代数学的不同领域和计算机科学中占有重要地位。例如，在形式语言和自动机理论中的语言对合半环[3]丰富了Kleene循环运算理论。近年来，Dolinca对合半群和对合半环领域做了大量的研究[4-6]，文献[2]对K-正则半环做了深入细致的刻画.本文受此启发，在K-正则半环上引入对合*运算，研究了K-正则半环的一个子类对合K-正则半环，对合半群的幂半环是对合K-正则半环当且仅当对合半群是对合正则半群，最后给出了对合正则半群的幂半环是对合交换半环的几个等价命题。

首先，介绍一些概念和术语。

设(S,+,·)是半环，记它的加法和乘法幂等元的集合分别为E+(S)和E·(S)，这里

E+(S)={e|e+e=e},E·(S)={e|e2=e},

用Sl+表示加法是半格的半环簇。对任意S∈Sl+，S中的元素e称为K-幂等元，是指e+e2=e2，S的全体K-幂等元构成的集合记为EK(S)。类似于正则半群上的Green-关系，我们定义K-正则半环上的两个Green-关系如下：

∀a、b∈S,

本文未涉及的其他概念和符号请参见文献[7-9]。

2　对合K-正则半环的等价刻画

本节将给出对合K-正则半环的等价刻画，为此先给出引理1。

引理1设(S,+,·,*)∈Sl+，且a、b、c、d∈S，

(1)若存在x1、x2、y1、y2∈S,使得a+x1by1=x2by2,则

a+(x1+x2+y1+y2)b(x1+x2+y1+y2)=(x1+x2+y1+y2)b(x1+x1+y1+y2),

(2)若存在x、y∈S,使得a+xby=xcy,则

a+(x+y)(b+c)(x+y)=

(x+y)(b+c)(x+y)。

(3)若存在x、y∈S,使得a+xcx=xcx,b+ydy=ydy,则

a+(x+y)(c+d)(x+y)=

(x+y)(c+d)(x+y),

b+(x+y)(c+d)(x+y)=

(x+y)(c+d)(x+y)。

(4)若a+b=b,c+d=d,则ac+bd=bd。

证明(1) 设u=x1+x2+y1+y2,则

x1by1+ubu=x2by2+ubu=ubu,

所以a+x1by1+ubu=x2by2+ubu,即a+ubu=

ubu, 且

a*+u*b*u*=(a+ubu)*=

(ubu)*=u*b*u*。

(2)

xby+(x+y)(b+c)(x+y)=

xcy+(x+y)(b+c)(x+y)=

(x+y)(b+c)(x+y),

a*+(x*+y*)(b*+c*)(x*+y*)=

a*+(x+y)*(b+c)*(x+y)*=

[a+(x+y)(b+c)(x+y)]*=

[(x+y)(b+c)(x+y)]*=

(x*+y*)(b*+c*)(x*+y*)。

(3)

xcy+(x+y)(b+c)(x+y)=

xdy+(x+y)(b+c)(x+y)=

(x+y)(b+c)(x+y)。

类似(2)，可证明

a*+(x*+y*)(c*+d*)(x*+y*)=

(x*+y*)(c*+d*)(x*+y*),

b*+(x*+y*)(c*+d*)(x*+y*)=

(x*+y*)(c*+d*)(x*+y*)。

(4) 事实上，由ac+bc=bc,得ac+b(c+d)=b(c+d),所以ac+bd=bd,且

a*c*+b*d*=(ca)*+(db)*=

(ca+db)*=(db)*=b*d*。

设(F,·,*)是对合半群，令S=P(F)是F的幂集,定义A+B=A∪B，AB={ab|a∈A,b∈B}。由F上的对合*运算诱导它的幂集上的*运算为A*={a*|a∈A},则(S,+,·,*)是对合半环，且S∈Sl+。

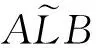
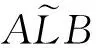
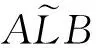
定理2设(F,·,*)是对合半群，则半环(P(F),+,·,*)是对合K-正则半环当且仅当(F，·,*)是对合正则半群。

证明设(P(F),+,·,*)是对合K-正则半环，任取a*∈S，则A*={a*}∈P(F)，于是存在X*∈P(F)，使得A*+A*X*A*=A*X*A*，即A*⊆A*X*A*。故存在x*∈X*，使得a*=a*x*a*，于是(F,·,*)是对合正则半群。

反之，设(F,·,*)是对合半群A*∈P(F)，则对任意a*∈A*，存在x*∈F，使得a*=a*x*a*，对于这样的x*记为xa，则X*={xa|a∈A}∈P(F)。故A*⊆A*X*A*，即A*+A*X*A*=A*X*A*，因此(P(F),+,·,*)是对合K-正则半环。

3　正则半群的幂半环是

对合交换半环

设(S，+,·,*)是对合K-正则半环，若它的K-幂等元e、f可交换，任取a、b∈S，存在x、y、z∈S，使得a+axa=axa,b+byb=byb,ab+abzab=abzab,于是zab+zabzab=zabzab,abzab+abzabzab=abzabzab,从而ab+abzabzab=abzabzab。由引理1可知，令t=x+y+abz+zab,则a+ata=ata,b+btb=btb,ab+abtab=abtab,这里ta、bt∈EK(S)，故tabt=bt2a,ab+bt2a=bt2a,于是我们可得到下述定理。

定理3设(S,+,·,*)是对合K-正则半环，对任意e、f∈EK(S),ef=fe,则对任意a、b∈S存在x∈S使得ab+bxa=bxa。

定理4设(F,·,*)是对合正则半群，则下列命题等价：

(1)P(F)的K-幂等元可交换；

(2) (F,·,*)是对合交换半群；

(3) (P(F),+,·,*)是对合交换半环。

证明易证明(2)⟹(3),(3)⟹(1)，下面只给出(1)⟹(2)的证明。

设a*∈F,e2=e∈F，则{a*}、{e}∈P(F),由定理3知，存在X*、Y*∈P(F)，使得

{e}{a*}+{a*}X*{e}={a*}X*{e},

{a*}{e}+{e}Y*{a*}={e}Y*{a*},

于是存在x*、y*∈X*,使得

ea*=a*x*e,a*e=ey*a*,所以

ea*e=a*x*e2=a*x*e=ea*,

ea*e=e2y*a*=ey*a*=a*e,

从而a*e=ea*,因此(F,·,*)是Clifford-半群。

于是F=[L,Gα,Φα,β,*]是群的对合强半格，且ab=(aΦα,αβ)(bΦβ,αβ),a∈Gα,b∈Gβ,aΦα*,β*=((a*)Φα,β)*。设eα*是Gα*的单位元，a、b∈Gα*，则A={eα*,a},B={eα*,b}∈P(F),且A、B是P(F)的K-幂等元，故AB=BA，即

{eα*,a,b,ab}={eα*,a,b,ba}。

若a=eα*或b=eα*,则ab=ba,又ab≠a,ab≠b,于是要么ab=eα*,要么ab=ba;若ab=eα*,则b=a-1,即a是b的逆元。总之ab=ba,从而Gα*是阿贝尔群，对任意α*∈L,a∈Gα*,b∈Gβ*,

ab=(aΦα*,α*β*)(bΦβ*,α*β*)=

(bΦβ*,α*β*)(aΦα*,α*β*)=ba，

于是(F,·,*)是对合交换半群。

[1] DOLINKA I. Idempotent distributive semirings with involution[J].International Journal of Algebra and Computation,2003,5:597-625.

[2] SEN M K, BHUNIYA A K. On semirings whose additive reduct is a semilattice[J].Semigroup Forum, 2011, 82:131-140.

[3] JONSSON B.The theory of binary relations[M]∥HALMDS P R.Algebraic Logic.Amsterdam:North-Holland,1991:245-292.

[4] DOLINCA I,VINCIC M. Involutorial Plonka sums[J].Periodica Mathematica Hungarica,2003, 46(1):17-31.

[5] DOLINCA I. On the lattice of varieties of involution semigroups[J].Semigroup Forum, 2001, 82:438-459.

[6] DOLINCA I. All varieties of normal bands with involution[J].Periodica Mathematica Hungarica,2000, 40:109-122.

[7] HOWIE J M. Fundamentals of semigroup theory[M].Oxford: Clarendon Press,1995.

[8] HOWIE J M. Automata and languages[M].Oxford: Clarendon Press, 1991.

[9] NORDAHL T E,SCHEIBLICH H E. Regular *-semi-groups[J].Semigroup Forum,1978,16:369-377.

〔责任编辑宋轶文〕

K-regular semiring with involution

FENG Junqing*, XU Hui

(College of Science, Air Force Engineering University,Xi′an 710051, Shaanxi, China)

Some properties onK-regular semiring with involution are studied.TheK-regular semiring with involution are discussed in different ways by using Green-relation onK-regular semiring.The power semiring of semigroup with involution which is aK-regular semiring with involution if and only if semigroup is a regular semigroup.Finally,it is obtained that the equivalent proposition of the power semiring of involutorial regular semigroup which is a commutative semiring with involution.

K-regular semiring with involution;K-idempotents; idempotent semiring; power semiring

1672-4291(2016)04-0014-03

10.15983/j.cnki.jsnu.2016.04.144

2015-07-09

陕西省自然科学基金(2014JQ1014)； 国家自然科学基金(61402364)

冯军庆，男，讲师。E-mail: fjq_0213@126.com

O152.7

A