分析·解答·结论·联想·运用—以2022年一道高考填空压轴题为线索的复习教学设计

安徽省太湖中学(246400) 李昭平

1 题目

已知x = x1,x = x2分别是函数f(x) = 2ax- ex2(a＞0,且a ≠ 1)的极小值和极大值点.若x1＜x2,则a的取值范围是______. (2022年高考全国乙卷理科第16题)

2 分析

本题结构新、立意新、解法新,具有较大难度.主要有三个特点:一是从结构形式上看,跳出了过去常见的ex模型,而以一般的指数函数ax与二次函数的复合型函数形式出现;二是从设置方式上看,属于逆向设置,由已知抽象的极小值点和极大值点,反过来确定待定参数a的取值范围;三是从解题思路上看,要研究f′(x) = 0有两根x1,x2,且在x1附近f′(x)左负右正,在x2附近f′(x)左正右负,靠继续求导研究f′′(x)的符号,比较复杂,思路受阻.这让我们联想到:能否直接将方程f′(x) = 2lna·ax- 2ex = 0“一分为二”成两个函数,即axlna = ex,利用函数y = axlna(动曲线)和y = ex(定直线)的图象的交点个数和位置来解决问题呢?基于这种想法,得到下述解答.

3 解答

由f′(x) = 2axlna - 2ex =0得, axlna = ex.令g(x) =axlna,h(x) = ex,则x1,x2应是这两个函数图象两个交点的横坐标.函数g(x) = axlna的图象形状与位置由参数a确定,必须对a分类讨论.

(1)若a＞1,则从如图1可以看出,在x1左边附近, g(x)＞h(x),即f′(x)＞0;在x1右边附近,g(x)＜h(x), f′(x)＜0.因此x1是极大值点,不合题意.

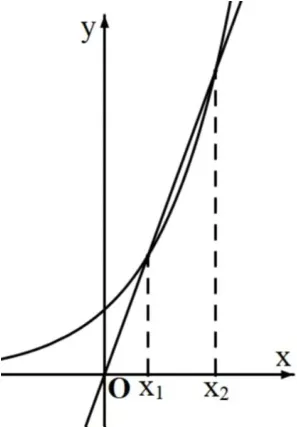
图1

(2)若0＜a＜1,则从如图2可以看出, x1,x2分别是极小值点和极大值点,符合题意.

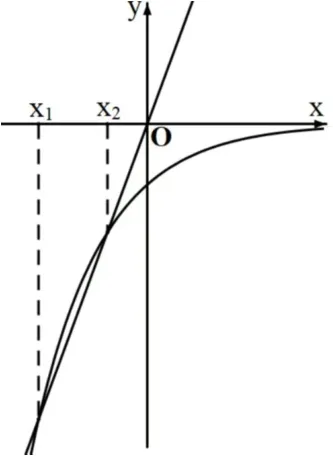
图2

显然,当曲线y = g(x)过原点的切线斜率小于直线h(x)的斜率e时,才能保证曲线y = g(x)与直线y = h(x)相交于两点.设切点为(x0,ax0lna), g′(x) = axln2a,g′(x0) =ax0ln2a.则= ax0ln2a,x0== logae.于是eln2a＜e,-1＜lna＜0,＜a＜1.故a的取值范围是

4 结论

由上述解答,得到以下结论:设φ(x) = g(x) - h(x),则φ(x)的零点⇔φ(x) = 0的实数根⇔g(x)与h(x)图象交点的横坐标.其中y = g(x)和y = h(x)是定曲线(含直线)或动曲线(含直线).这里的y = h(x)可以是函数f(x)或f′(x)等等.对于关于含有参数的函数φ(x),要研究其零点、单调性、极值、最值、图象等,往往涉及到φ(x) = 0的实数根问题,以及不等式g(x)＞h(x)(或g(x)＜h(x))问题,利用“一分为二、图象交点”的思想方法将复合型函数方程φ(x) = 0或不等式φ(x)＞0(φ(x)＜0),分成两条曲线y = g(x)和y = h(x),即g(x) = h(x)或不等式g(x)＞h(x)(g(x)＜h(x)),分类讨论参数确定图象的位置和交点的个数,常常能化繁为简、化难为易,顺利实现解题目标.

5 联想

5.1 改变条件

★将高考题中的条件“x1,x2分别是极小值和极大值点”改为“x1,x2分别是极大值和极小值点”,则得到:

联想1已知x = x1,x = x2分别是函数f(x) =2ax- ex2(a＞0,且a ≠ 1)的极大值和极小值点.若x1＜x2,则a的取值范围是______.

解析由高考题的解答知a＞1,如图1符合.显然,当曲线g(x)过原点的切线斜率小于直线h(x)的斜率e时,才能保证曲线g(x)与直线h(x)相交于两点.于是eln2a＜e,0＜lna＜1,1＜a＜e.故a的取值范围是(1,e).

★将高考题中的条件“x1,x2分别是极小值和极大值点”改为“没有极值点”,则得到:

联想2已知函数f(x) = 2ax- ex2(a＞0,a ≠ 1)没有极值点,则a的取值范围是______.

解析由高考题和联想1的解答知, a的取值范围是

★将高考题函数中的“a”与“e”互换位置,条件“x1,x2分别是极小值和极大值点”改为“x1,x2分别是极大值和极小值点”,则又得到:

联想3已知x = x1,x = x2分别是函数f(x) =2ex-ax2(a＞0且a ≠ 1)的极大值和极小值点.若x1＜x2则a的取值范围是______.

解析由f′(x) = 2ex- 2ax = 0得, ex= ax.令g(x) = ex,h(x) = ax,则x1,x2应是这两个函数图象两个交点的横坐标.观察图象可知,当曲线g(x)过原点的切线斜率小于直线h(x)的斜率a时,才能保证曲线g(x)与直线h(x)相交于两点.设切点为(x0,ex0),则= ex0,x0= 1.于是a＞e.故a的取值范围是(e,+∞).

注联想3则是我们常见的ex与二次函数的复合型,比高考题简单得多.

5.2 逆向思考

★对高考题作逆向思考,题设与结论互换得到:

联想4若＜a＜1,试判断函数f(x) = 2ax-ex2极值点的个数.

解析由高考题的解答知,如图2符合.当＜a＜1时,曲线g(x)过原点的切线斜率小于直线h(x)的斜率e,曲线g(x)与直线h(x)相交于两点,其横坐标为x1,x2,x1＜x2,x1为极小值点, x2为极大值点.

★对联想1作逆向思考,题设与结论互换又得到:

联想5若1＜a＜e,试判断函数f(x) = 2ax- ex2极值点的个数.

解析由高考题和联想1的解答知,如图1符合.x1＜x2, x1为极大值点, x2为极小值点.

5.3 类比引申

★将高考题函数中的“e”一般化为“b”,类比引申则得到:

联想6已知x = x1,x = x2分别是函数f(x) =2ax- bx2(a＞0, a ≠ 1,b＞0)的极小值和极大值点.若x1＜x2,则a的取值范围是______.

解析由高考题的解答知, a的取值范围是

注显然,当b = e时,就是高考题.

★将联想1函数中的“e”一般化为“b”,类比引申则得到:

联想7已知x = x1,x = x2分别是函数f(x) =2ax- bx2(a＞0,且a ≠ 1,b＞0)的极大值和极小值点.若x1＜x2,则a的取值范围是_____.

解析由联想1的解答知, a的取值范围是

注显然,当b = e时,就是联想1.

★ax与logax互为反函数,是一对孪生兄弟,将高考题函数中的“ax”变为“logax”,适当改变条件,又得到:

联想8已知函数f(x) = 2logax-ex2(a＞0,且a ≠ 1)有唯一极值点,则a的取值范围是_____.

解析由联想8的解答知, a的取值范围是(0,1).

6 运用

6.1 处理零点问题

例1(2022年高考全国乙卷理科第21题)已知函数f(x) = ln(1 + x) + axe-x,a∈R.

(1)当a = 1时,求曲线y = f(x)在点(0,f(0))处的切线方程;

(2)若f(x)在区间(-1,0),(0,+∞)各恰有一个零点,求a的取值范围.

解析(1)易得曲线y = f(x)在点(0,f(0))处的切线方程为y = 2x,过程从略.

(2)函数f(x) = ln(1 + x) + axe-x的定义域是(-1,+∞).由ln(1 + x) + axe-x= 0得到: exln(1 + x) =-ax.

令g(x) = exln(1 + x),h(x) = -ax.函数f(x)在区间(-1,0),(0,+∞)各恰有一个零点,即函数g(x)和函数h(x)的图象在区间(-1,0),(0,+∞)各恰有一个交点. g′(x) =ex[ln(1 + x) +],再令φ(x) = ln(1 + x) +,x＞-1,则由φ′(x) == 0解得x = 0.在(-1,0)内φ′(x)＜0,φ(x)单减;在(0,+∞)内φ′(x)＞0,φ(x)单增.因此φ(x)≥φ(0) = 1,g′(x)＞0, g(x)单增,且g(0) = 0, g(x)的图象如图3所示.

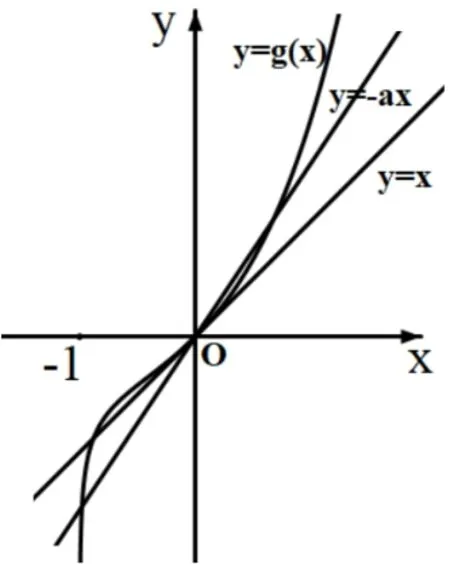
图3

g′(0) = 1,g(x)的图象在(0,0)处的切线是y = x.显然,当a＞0时,不合题意.当a＜0时,要保证曲线y = g(x)与直线y = h(x)在区间(-1,0),(0,+∞)各恰有一个交点,只要满足-a＞1,a＜-1.故a的取值范围是(-∞,-1).

点评将方程ln(1 + x) + axe-x= 0“一分为二”成exln(1+x) = -ax处理,比“一分为二”成或a = -处理简单得多.

6.2 处理极值点问题

例2(2022年安徽合肥模考题)若函数f(x) =axlnx - ex存在唯一的极值点,则实数a的取值范围是______.

解析由题意知, f′(x) = alnx + a - ex= 0有唯一正实数根,即alnx + a = ex有唯一正实数根.令g(x) = alnx + a,h(x) = ex,其图象在第一象限只能有唯一公共点.

当a＞0时(如图4),在x0附近,始终有g(x)＞h(x),则f′(x)＞0,保号,此时x0不是f(x)的极值点.当a＜0时(如图5),在x0附近, f′(x)异号.此时x0是f(x)唯一的极值点.故实数a的取值范围是(-∞,0).

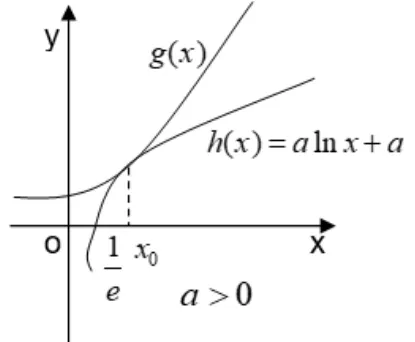
图4

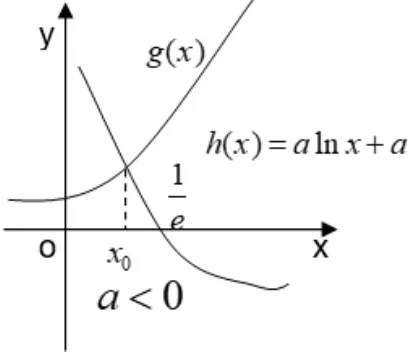
图5

点评本题考查函数的极值点问题,是对数函数与指数函数的复合型函数,“一分为二”成两个函数y = g(x)(动曲线)和y = h(x)(定曲线),则立即转化为动曲线与定曲线的位置关系与交点个数问题,结合极值点的含义(在极值点两旁附近f′(x)异号),确定参数a的取值范围.

6.3 处理图象交点问题

例3(2021年高考全国甲卷第21题)已知a＞0且a ≠ 1,函数f(x) =

(1)当a = 2时,求f (x)的单调区间;

(2)若曲线y = f (x)与直线y = 1有且仅有两个交点,求a取值范围.

6.4 处理恒成立问题

例4(2022年新高考Ⅱ卷第22题)已知函数f(x) =xeax- ex,a∈R.

(1)当a = 1时,讨论f(x)的单调性;

(2)当x＞0, f(x)＜-1,求a的取值范围;

(3)设n∈N∗,证明:

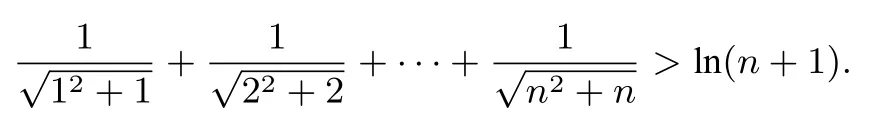
解析(1) f(x)的单增区间是(0,+∞),单减区间是(-∞,0).过程从略.

成立.

点评本题考查恒成立不等式中的参数范围和数列不等式,利用“一分为二”思想,将原不等式化成＞eax(x＞0),研究两个函数图象的位置关系与交点个数.涉及到极限位置、洛必达法则和函数不等式的特殊化(特殊化成数列),有较高的思维深度和运算难度,直观想象、逻辑推理和数学运算三种核心素养贯穿其中.

6.5 处理能成立问题

例5(2022年江西南昌模考题)设f(x) = x+xlnx.若存在x1＞1,使得2f(x1) - (k + 1)x1+ k＜0成立,则整数k的最小值是_____.

解析2f(x) - (k + 1)x + k＜0⇔f(x)＜-

图6

以上我们从一道最新高考题出发,通过分析、解答,归纳出“一分为二、图象交点”的解题思想方法.再通过九个联想和五种运用,强化对这种思想方法的认识与理解.在整个过程中,融观察分析、直觉逻辑、提炼概括、猜想证明于一体,锤炼了数学思维,拓宽了解题空间.其关键点是“一分为二”成什么形式比较恰当,这需要我们去认真思考、认真实践和认真感悟.由此可见,对一道好的高考题进行多方向、多侧面、多角度研究,运用到复习课堂上,必能收获丰盈,并让学生充分感受数学高考题的巨大魅力.