平移齐次化解高考全国卷圆锥曲线题及其推广

广东省湛江一中培才学校(524037) 魏 欣

平移齐次化方法在解决圆锥曲线中关于斜率之和或积为定值的问题,是通过坐标系的平移,过任意点的直线斜率问题均可转化为过原点的斜率问题,齐次联立直线方程与圆锥曲线方程转化为关于的一元二次方程,进而由根与系数的关系来求解,可以避免繁琐运算,提高解题正确率.

一、平移齐次化的解法

如图1所示,设O′在原坐标系中的坐标为(h,k),平移原坐标系,得到以O′为原点的新的坐标系x′o′y′.设M在原坐标系中的坐标为(x,y),在新坐标系中的坐标为(x′,y′),则坐标平移公式

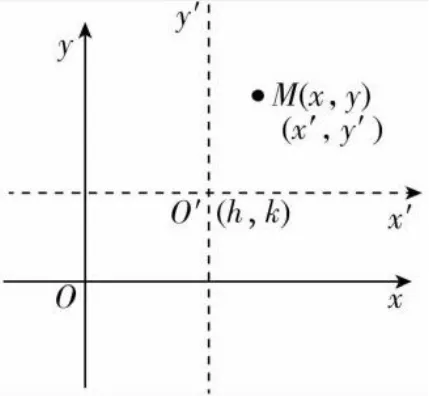
图1

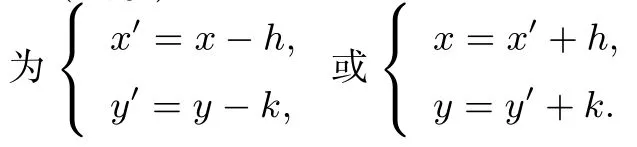
据此,可以得到平移齐次化解圆锥曲线问题的一般解法是:若直线l : ax + by + c = 0与圆锥曲线C : f(x,y) = 0相交于两点,联立方程将直线方程适当变形,代入圆锥曲线方程式,总可以消去一次项及常数项,得关于x,y的齐次方程:

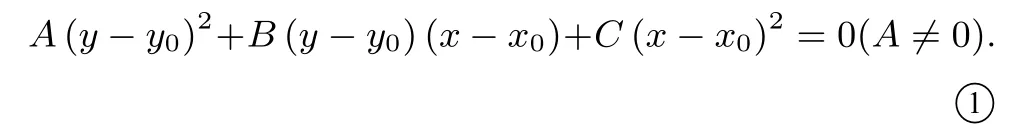
设P (x0,y0)为平面上一定点,若不重合两点P1(x1,y1),P2(x2,y2)的坐标满足方程①,则将方程①变形为:

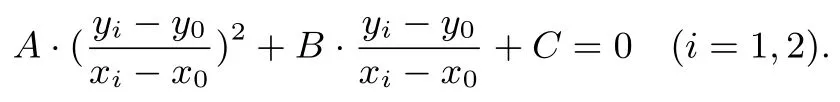
P1(x1,y1),P2(x2,y2)的坐标满足方程①,即有

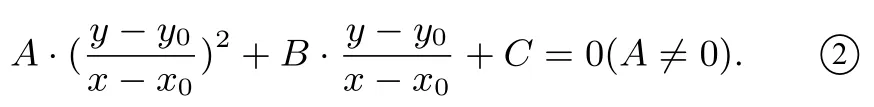
由韦达定理可以得到以下结论:

(1)若直线PP1与直线PP2的倾斜角互补,则由kPP1+ kPP2= 0⇔B = 0.

(2)若直线PP1与直线PP2相互垂直,则由kPP1·kPP2= -1⇔A + C = 0.

(3)若直线PP1与直线PP2的斜率之和为m,则由kPP1+ kPP2= m⇔Am + B = 0.

(4)若直线PP1与直线PP2的斜率之积为n,则由kPP1·kPP2= n⇔An - C = 0.

二、平移齐次化解圆锥曲线高考题的解法探究

下面通过近年的高考题为例加以阐述.

例1(2022年高考全国I卷第21题)如图2所示,已知点A(2,1)在双曲线C := 1(a＞1)上,直线l交C于P,Q两点,直线AP,AQ的斜率之和为0.

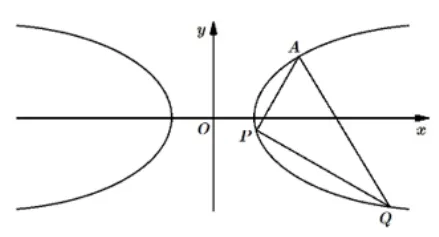
图2

(1)求l的斜率;

解析(1)易求双曲线C的方程为= 1.如图3所示,将原坐标系平移成以点A(2,1)为原点的的坐标系,记新原点为O′,点P,Q分别对应点,则坐标平移公式为双曲线C := 1对应C′:- (y′+ 1)2= 1.

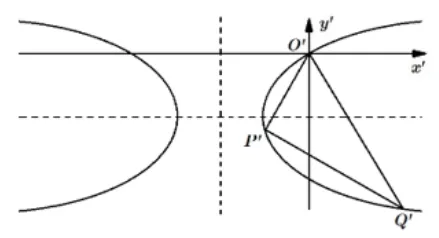
图3

考虑到直线l不经过点A,故与直线l对应的l′不经过O′,故可设l′的方程为mx′+ ny′= 1.将直线l′与双曲线C′的方程联立代换常量“1”,齐次化得

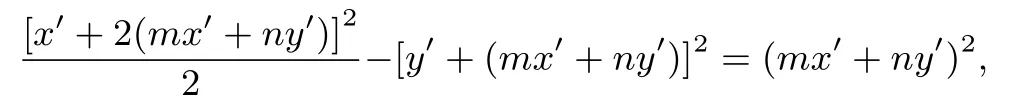
整理得

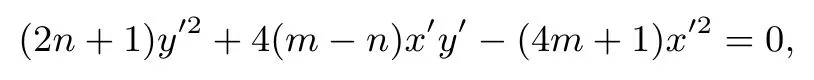
方程两边同除以x′2得

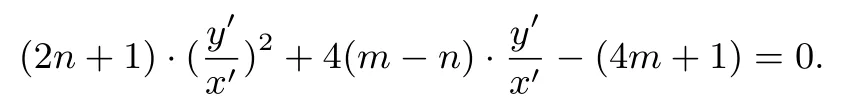
点评本题第(1)问利用平移齐次化方法迅速求解后,第(2)在此基础上顺势而下,直接利用平移后的坐标系进行求解.此种平移齐次化解法实际上是简化运算的技巧.

例2(2021年高考全国I卷第21题)在平面直角坐标系xOy中,已知点点M满足|MF1| - |MF2| = 2,记M的轨迹为C.

(1)求C的方程;

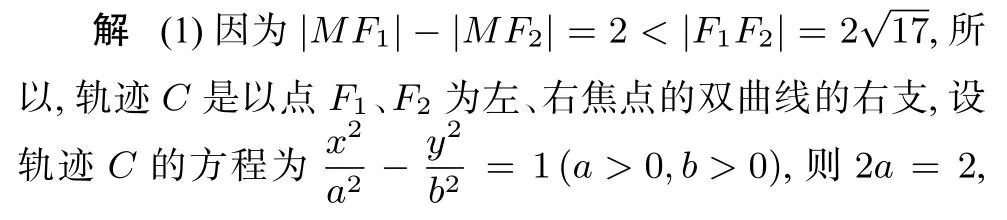
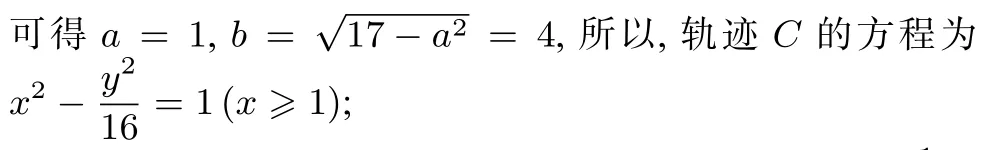
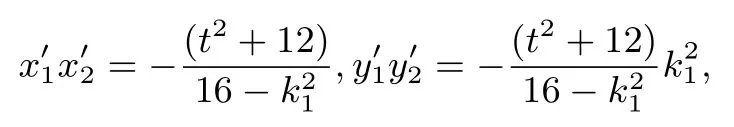
点评坐标系平移前后,直线的斜率、角的大小、线段的长度与图形的面积均未发生改变,思路还是原来的思路,但通过平移坐标系大大简化了运算的难度,对于思维水平好的同学来说,不失为一种考试节省时间的解法.

例3(2020年高考全国I卷第20题)如图4所示,已知A、B分别为椭圆E := 1(a＞1)的左、右顶点, G为E的上顶点,= 8, P为直线x = 6上的动点, PA与E的另一交点为C, PB与E的另一交点为D.

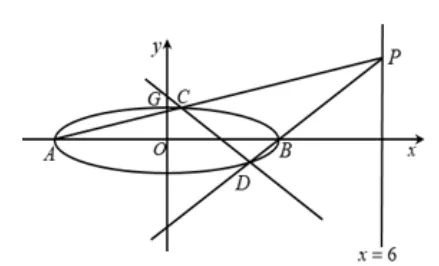
图4

(1)求E的方程; (2)证明:直线CD过定点.

解析(1)= 1(过程从略) ;

(2)证明:如图5所示,连接BC,不妨设PA,PB,BC斜率为k1,k2,k3, C(x0,y0),P(6,t0),由k1=则k =23k1,且k1·k3=如图6所示.

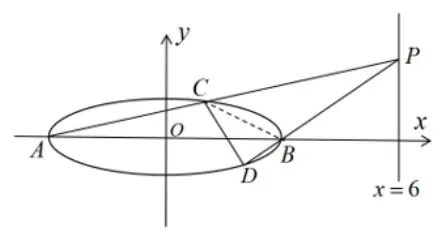
图5

图6

将椭圆E : x2+9y2= 9和直线CD沿n = (-3,0)平移变换,得到曲线E2: (x + 3)2+9y2= 9,即x2+9y2+6x = 0,

点评上述平移齐次化的解法可谓是“大道至简”,利用了过原点直线的斜率的简洁特性,也展现了截距式直线方程在解题中的妙用,大大降低了运算,揭示了圆锥曲线问题的本质,同时也促进了学生数学运算和直观想象数学素养的发展.

例4(2020年新高考I卷第22题)已知椭圆C := 1(a＞b＞0)的离心率为,且过点A(2,1).

(1)求C的方程:

(2)点M, N在C上,且AM⊥AN, AD⊥MN, D为垂足.证明:存在定点Q,使得|DQ|为定值.

解(1)由题意知:= 1.易得椭圆方程为:

因为A,F为两个定点,所以|AF|为定值.又因为AD⊥MN,所以D在|AF|为直径的圆上,取AF中点为Q点,存在,使得|DQ|为定值.

点评上述平移齐次化的解题过程可以归纳为两步:一是由直线与圆锥曲线方程得到齐次式y2= (x - my)x,这是通过代换椭圆方程中的常量“1”实现的,而不是消去x或y,这是与常规的联立的不同所在,也是齐次化处理的关键一步;二是将齐次式变形成关于的一元二次方程,这样方程的两根即为斜率kOA与kOB.

例5(2018年高考全国I卷理科第20题)如图7所示,设椭圆C := 1的右焦点为F,过F的直线l与C交于A, B两点,点M的坐标为(2,0).

图7

(1)略; (2)设O为坐标原点,证明:∠OMA =∠OMB.

解(2)如图8所示,将椭圆E : x2+2y2= 2和直线CD沿n = (-2,0)平移变换,得到曲线E′: (x + 2)2+ 2y2= 2,即x2+ 2y2+ 4x + 2 = 0.

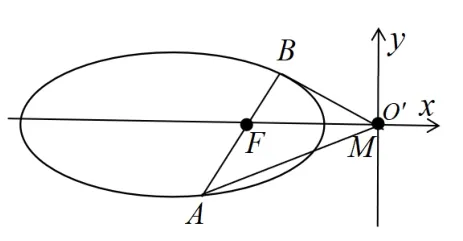
图8

(1)求C的方程;

(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为-1,证明: l过定点.

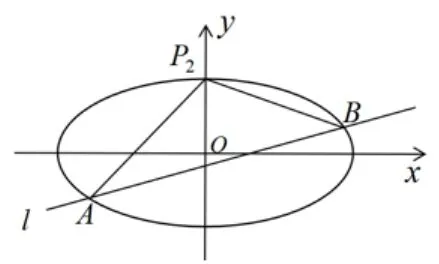
图9

解(1) C的方程为+ y2= 1(过程从略).

(2)如图10所示,将椭圆C : x2+ 4y2= 4和直线l沿n = (0,-1)平移变换,得到曲线C2: x2+4(y + 1)2= 4,即x2+ 4y2+ 8y = 0.

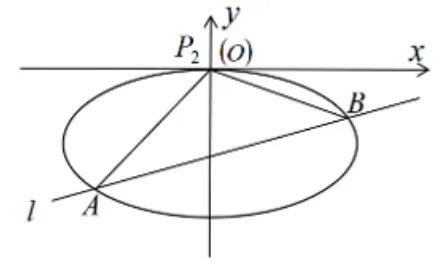
图10

设l经过变换后的直线l′: mx + ny = 1,代入上述方程齐次化得x2+ 4y2+ 8y (mx + ny) = 0,整理后得+ 1 = 0,设平移后A(x3,y3),B (x4,y4),而P2(0,0),由题意,根据韦达定理有- 1,即m = n +,即l′:(n +)x + ny = 1,故直线l′过定点T′(2,-2),将直线l′沿-n = (0,1)变换为l,则直线l过定点T (2,-1).

点评用平移齐次化的思想处理该题,其目的是便捷的利用“两斜率之和为定值”的条件,但方程的代换和化简是一个难点,学生比较难想到,这需要教师给出一个示范解答,而学生掌握这种方法的意义在于拓展该方法能处理的其它题型范围.

三、平移齐次化解圆锥曲线问题的结论推广

根据以上解法探究,可以将圆锥曲线问题推广到一般的情况,得到平移齐次化方法在解决圆锥曲线中关于斜率之和或积为定值的问题的结论.

结论1已知椭圆C := 1(a＞b＞0)上的定点P(x0,y0),动点A, B(不同于P),直线PA与PB的斜率之和为λ(λ为定值).

(2)当λ= 0且y0≠ 0时,直线AB的斜率为

(3)当λ= 0且y0= 0时,直线AB的斜率不存在.

图11

整理得

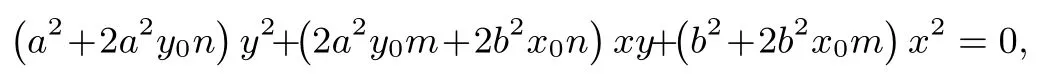
两边同时除以x2,得

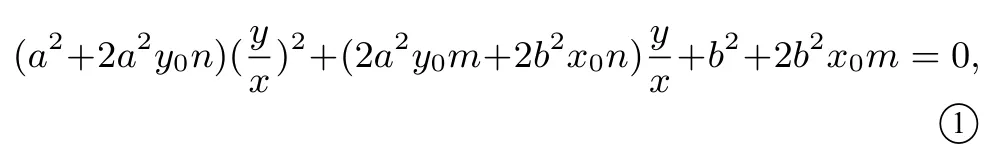
易知k1, k2是方程的两个解,

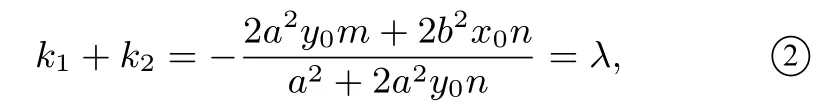
联立直线方程mx + ny = 1,得

证明由结论1的分析过程①式知,

联立方程mx + ny = 1,得

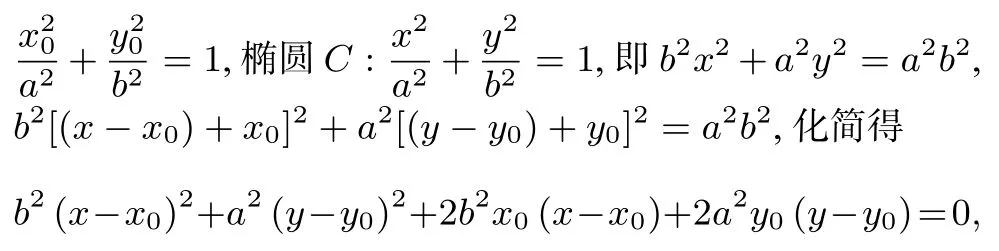
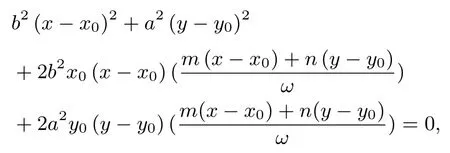
化简得,

以上有关双曲线的结论的证明可类比于椭圆的证法,此处从略.

结论9已知抛物线C :y2= 2px(p＞0)上的定点P(x0,y0),动点A, B(不同于P),直线PA与PB的斜率之和为λ(λ为定值).

(2)当λ= 0且y0≠ 0时,直线AB的斜率为-

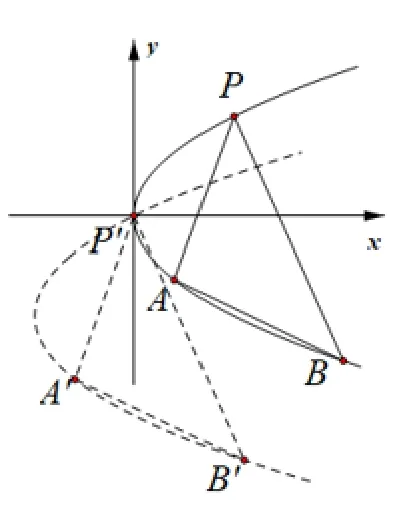
图12

(3)当λ= 0且y0= 0时,直线AB的斜率不存在.

结论10、11、12的证明与结论9的方法类似,此处从略.

平移齐次化方法充分体现了运用坐标法求解圆锥曲线综合问题的整体构思,平移齐次化联立能得到什么样的结论、解决什么样的问题,平移齐次化又能达到什么样的效果,平移后的“变”与“不变”怎样来解释平移前的问题.只有对平移齐次化方法有了整体的认知,才能将求解的思路形成一个整体构思,从而大大降低了运算,揭示了圆锥曲线问题的本质,从而更好地提升学生的数学运算和直观想象的数学素养.