2022年高考理科数学甲卷第16题的探究与变式

广东省中山市桂山中学(528463) 谭天众

1 题目呈现

题目(2022年高考理科数学甲卷第16题)已知ΔABC中,点D在边BC上,∠ADB = 120°, AD = 2, CD = 2BD.当取得最小值时,.

本题为是填空题的压轴题,涉及不常见线段比例问题,考查余弦定理、基本不等式、对勾函数、导数等知识点,综合性强,对学生来说有一定难度,对学生的思维能力、运算能力、推理能力都提出了要求.

2 一题多解

2.1 求表达式

解法1(余弦定理)如图1,设BD = x,在ΔADC中应用余弦定理得: AC2= 4 + (2x)2- 2×2×2xcos60°=4x2-4x+4;在ΔABD中, AB2= x2+4-2x×2cos120°=x2+ 2x + 4.则.

图1

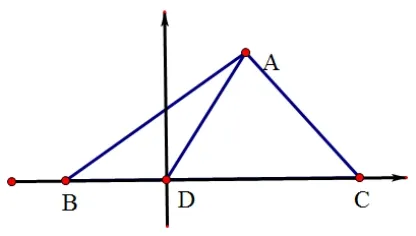
图2

2.2 求最值条件

解法1(基本不等式)

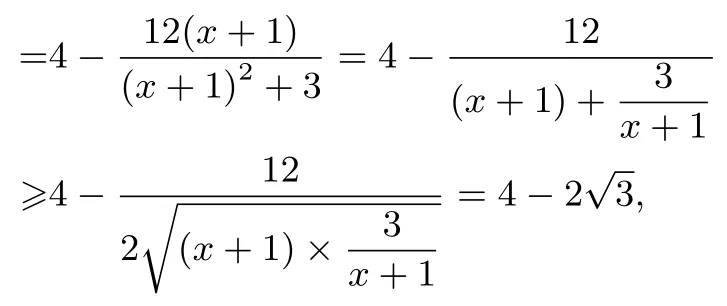
解法3(导数法)

2.3 题目另解

托勒密不等式凸四边形的两组对边乘积之和大于等于对角线的乘积,当且仅当凸四边形有外接圆时取得等号.如图3,已知凸四边形ABCD中, AB·CD + AD·BC≥AC·BD,当且仅当A,B,C,D共圆时取得等号.

图3

设点B关于直线AD的对称为点E,如图4,由对称性, AB = AE, DB = DE,∠ADB =∠ADE = 120°,所以∠CDE =∠ADE -∠ADC = 60°,设BD = x,则

图4

由托勒密不等式, AB·CE + BE·AC≥AE ·BC,即≥AB·3x,则当且仅当A,B,E,C共圆时取得等号.共圆时,由于AD为线段BE的垂直平分线,所以圆心O在AD上,因为EB = EC,所以OE⊥BC,所以∠DOE =∠DEO = 30°,所以DO = DE = x,∠BOE = 60°,从而ΔOBE为等边三角形,则AD = OA + OD,即2 =+ x,得x =- 1,所以BD =- 1.

3 题目一般化

已知ΔABC中,点D在边BC上,如图1,设∠ADC =α, BD = x, AD = y, CD =µBD,考虑的最值情况,以及当其取最值时的条件.

探究1将t看成变量,µ与α为固定量.

探究2将µ看成变量, t与α为固定量.

易见t2+ (2cosα)t + 1 = (t + cosα)2+ 1 - cos2α＞0.

探究3将α看成变量, t与µ为固定量.

4 题目改编

应用以上探究结论,可以将原题改编,得到以下变式,供学生练习.