从射影几何视角看2022年高考甲卷第20题

云南师范大学数学学院(650500) 陈碧兴 马绍文

题目(2022年高考甲卷第20题)设抛物线C : y2=2px(p＞0)的焦点为F,点D(p,0),过点F的直线交C于M, N两点.当直线MD垂直于x轴时, |MF| = 3.

(1)求C的方程;

(2)设直线MD, ND与C的另一个交点分别为A, B,记直线MN, AB的倾斜角分别为α,β.当α-β取得最大值时,求直线AB的方程.

简析易得C的方程为y2= 4x.可使用常规的解析方法求解第(2)问.设出A, B, M, N四点的坐标,根据直线斜率、韦达定理、三点共线等条件表示出tan(α-β),从而转化为解不等式问题,此方法符合高中学生的认知,思路清晰,但计算繁琐.

其实本题含有丰富的射影几何背景,克莱因曾说:基础数学的教师应该站在更高的视角来审视、理解初等数学问题,只有观点高了,事物才能显得简单明了[1].下面针对第(2)问给出射影几何理论下的两种解法,供广大教师参考,首先给出射影几何中的部分相关理论.

1 射影几何相关理论[2]

1.1 点列交比

特别地有:一线段被它的中点和这直线上的无穷远点所调和分割.

1.2 线束交比

若a, b, c, d是共点的四条直线,则(ab,cd) =叫做a, b, c, d的交比,若(ab,cd) = -1,则称a, b, c, d为调和线束.

特别地有: (1)若任意一条直线s截线束a, b, c, d于点A, B, C, D,则有(ab,cd) = (AB,CD).

(2)若共点四直线a, b, c, d的斜率分别为k1, k2, k3, k4,则(ab,cd) =.

(3)交比经中心射影后不变.

1.3 极点极线理论

如图1,如果不在二次曲线Γ上的两点M, N的连线被它和Γ的交点P1, P2所调和分割,则称两点M, N关于二次曲线Γ成共轭点.

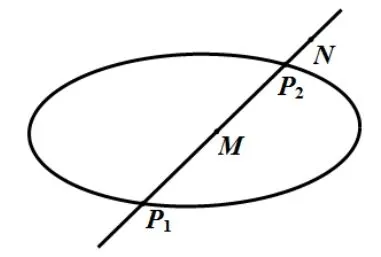
图1

通过一已知点P引诸直线,这些直线与Γ的每一对交点有P的一个调和共轭点,即P关于Γ的一个共轭点.这些共轭点的轨迹是一条直线,称为点P的极线,点P称为这条直线的极.

如图2, P为不在二次曲线上的点,过点P引两条割线依次交二次曲线于点E, F, G, H连接EH, FG交于点N,连接EG, FH交于点M,则MN为点P对应的极线.特别地,若P是二次曲线上的点,则过点P的切线即为极线.同理直线PN为点M对应的极线,直线PM为点N对应的极线[3].

图2

设二次曲线方程为: Ax2+ Cy2+ 2Dx + 2Ey + F = 0,则点(x0,y0)对应的极线方程为Ax0x+Cy0y+D(x0+x)+E(y0+ y) + F = 0.特别地有:

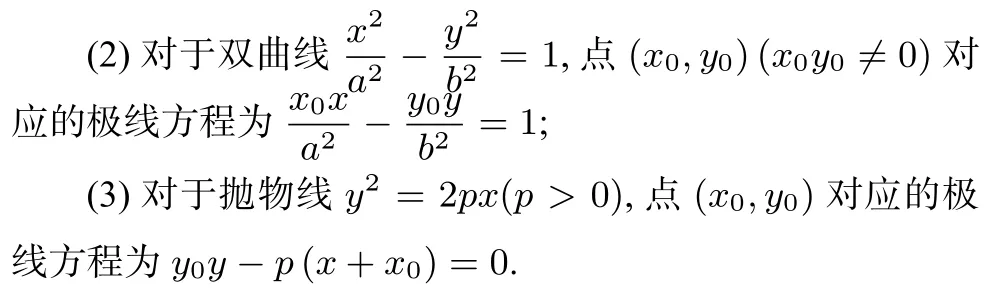
2 射影几何背景下的两种解法

2.1 第一种解法

当直线MN斜率不存在时,α=β= 90°,此时α-β= 0.

要使α-β最大,则tan(α-β)最大,且易知当直线MN,AB的斜率为正时,α-β为正才能达到最大.由基本不等√式可知,当且仅当tanβ=时, tan(α-β)最大,α-β取得最大值,此时直线AB的方程为x -- 4 = 0.

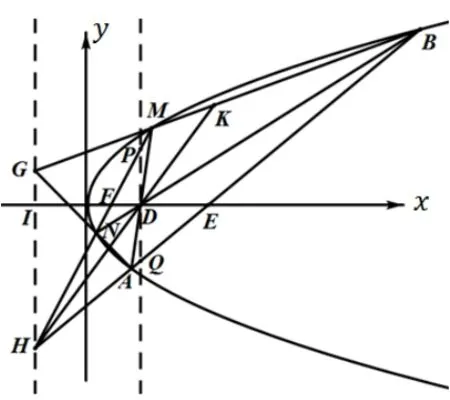
图3

在此解法中,由于交比在中心射影下不变,所以H(GK,MB) = H (D∞D,PQ) = -1(D∞为点D的无穷远点),即线段PQ被点D和点D的无穷远点调和分割,所以点D为PQ的中点.该结论由于其几何图形形似蝴蝶,被称为蝴蝶定理,最先于1815年英国的杂志《先生日记》中作为一个征求证明的问题首次刊出, 1944年,《美国数学月刊》第2期首次将其称为蝴蝶定理[4].该定理的证明方法数不胜数,至今仍被许多数学爱好者研究.

下面利用蝴蝶定理给出本题的第二种解法.

2.2 第二种解法

设直线MN方程为: y = mx - m,直线AB交x轴于点E,过点D作x轴的垂线分别交MN, AB于点P, Q,由极点极线的几何定义知GH为点D对应的极线,则GH方程为x = -2;又因为MN交GH于点H,则H(-2,-3m);由蝴蝶定理可得PD = QD,则P(2,m), Q(2,-m),所以|PQ| = 2m, |HP| =在ΔEFH中∠EFH = 180°-α,∠FEH =β,则∠EHF =α-β;所以

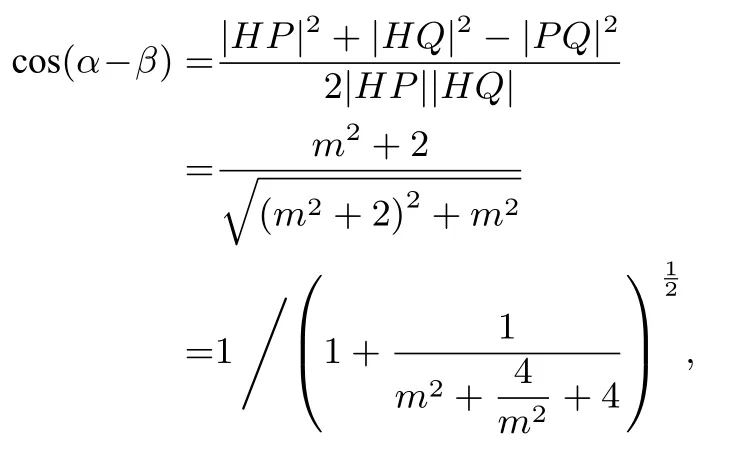
不难发现,本题中GH⊥x轴,且交点I与点D关于原点对称,α-β最大时,恰有kMN·kAB= 1.我们自然想到将题中的条件一般化之后,这些结论是否仍然成立?

3 试题中的结论

经过探究发现,点F、D为x轴上任意两点时,结论仍然成立,即有:

结论1设抛物线C : y2= 2px(p＞0),点F, D分别为x轴上任意两点,过点F的直线交C于点M, N,设直线MD, ND与C的另一个交点分别为A, B,直线BM, AN相交于点G,直线MN, AB相交于点H,直线GH交x轴于点I,则GH⊥x轴,且OI = OD.

证明设D(x0,0),由极点极线的几何定义知GH为点D对应的极线,则GH方程为x = -x0,所以GH⊥x轴,且OI = OD.

结论2设抛物线C : y2= 2px(p＞0),点F, D分别为x轴正半轴上任意两点,过点F的直线交C于点M, N,设直线MD, ND与C的另一个交点分别为A, B,记直线MN,AB的倾斜角分别为α,β,则当kMN·kAB= 1时|α-β|最大.

证明设D(x0,0), F(x1,0),直线MN方程为y =k(x - x1),直线MN, AB相交于点H;由结论1得H(-x0,-kx0- kx1),由蝴蝶定理得P(x0,kx0- kx1),Q(x0,-kx0+ kx1);则|PQ| = 2k(x0- x1), |HP| =在ΔPQH中

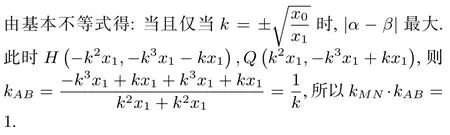
4 推广

结论1和结论2,还可以推广到椭圆和双曲线中,即有:

推广1设椭圆C := 1,点F, D分别为x轴上任意两点,过点F的直线交C于点M, N,设直线MD,ND与C的另一个交点分别为A, B,直线BM, AN相交于点G,直线MN, AB相交于点H,直线GH交x轴于点I,则GH⊥x轴,且OI·OD = a2.

推广2设双曲线C := 1,点F, D分别为x轴上任意两点,过点F的直线交C于点M, N,设直线MD,ND与C的另一个交点分别为A, B,直线BM, AN相交于点G,直线MN, AB相交于点H,直线GH交x轴于点I,则GH⊥x轴,且OI·OD = a2.

推广3设椭圆C := 1,点F, D分别为椭圆内坐标轴上任意两点,过点F的直线交C于点M, N,设直线MD, ND与C的另一个交点分别为A, B,记直线MN,AB的倾斜角分别为α,β,则当kMN·kAB= 1时|α-β|最大.

推广4设双曲线C := 1,点F, D分别为双曲线一支内部坐标轴上任意两点,过点F的直线交C于点M, N,设直线MD, ND与C的另一个交点分别为A, B,记直线MN, AB的倾斜角分别为α,β,则当kMN·kAB= 1时|α-β|最大.

椭圆和双曲线中的证明方法与抛物线相同,这里不再赘述.