磨损导致接触角变化对滚柱导轨副Archard模型的修正与仿真*

张巍，刘海亮，陈荣泽，付宏宇，索荣康

(1.内蒙古科技大学 工程训练中心，内蒙古 包头 014010；2.内蒙古科技大学 机械工程学院，内蒙古 包头 014010)

直线滚柱导轨副是重载机床的关键部件[1].针对其磨损的研究，张巍[2]研究了磨损量对滚动副各参数的影响规律.张赟[3]研究了油润滑下，4种微织构摩擦，实验证明微织构有一定的减摩能力.赵义鹏[4]考虑受垂直载荷下接触角变化，运用Archard、显微切削磨损理论分析了滚动导轨副的磨损过程.王民[5]分析了粘着磨损下，滚珠和滚道接触面微凸体的磨损过程，建立了滚珠和滚道接触面的分形磨损模型.Wang[6]建立了新的滚动导轨磨损系数计算模型.Zou[7]研究了滚动导轨的磨损对接触刚度的影响.根据磨损效应对滚珠在不同运行距离下接触变形的影响，其整体刚度衰减分为2个阶段.张巍[8]运用齐次变换矩阵，建立了考虑接触角变化的滚柱导轨副刚度模型，找到了接触角的变化对滚柱导轨副刚度曲线的影响规律.

借助Archard模型计算时忽略了接触角变化对磨损的影响.基于Palmgren公式，考虑变化的接触角建立了上、下排滑块变形模型.分析了磨损导致的接触角变化对上/下排载荷的修正和对磨损体积的修正.

1 滚柱-滚道接触分析

研究滚柱导轨副的磨损体积是研究其摩擦磨损性能的基础.随着磨损的加剧，滚柱的接触角也发生变化，同时会影响滑块的受力状态并导致磨损体积的变化.在精确的磨损计算时需要对接触角的变化导致的磨损量进行修正.

滚柱直线导轨副的滚柱与轨道之间的接触变形可视为1个有限长度的弹性圆柱体与1个刚度平面相接触产生的弹性变形.在滚柱回转中心建立坐标系Or.X为滚柱滚动方向，其正向为垂直于纸面向内，Y正向为水平向右，Z负向为铅锤方向，如图1所示.设α为滚柱与水平向偏角.l为滚柱有效接触长度，mm.Dd为滚柱回转直径，mm.

图1 滚柱坐标系建立

设Q为滚柱所受法向接触力.δ为法向力Q导致的滚柱与滚道单边变形量.δw为磨损导致的滚道法向位移量.如图2所示.由Palmgren公式可得：

(1)

式中：δ为滚柱中心相对导轨轨道的弹性变形量，mm；v为导轨材料的泊松比；E为导轨材料的弹性模量，GPa；Q为滚柱所受接触力，N.

设Qi/N为第i列滚柱所受法向接触力;δi/mm为第i列滚柱受Qi/N导致的滚柱初始变形量，i=1，2，3，4；Q0为滚柱所受法向初始预紧力，N；δ0为滚柱受初始预紧力导致的初始变形量，mm.Pw/N为滚道磨损量δw/mm所抵消的法向力.一般情况，滚动导轨副中滚动体的刚性远大于滚道的刚性.因此，认为滚柱不变形，变形和磨损全部由滚道承担.

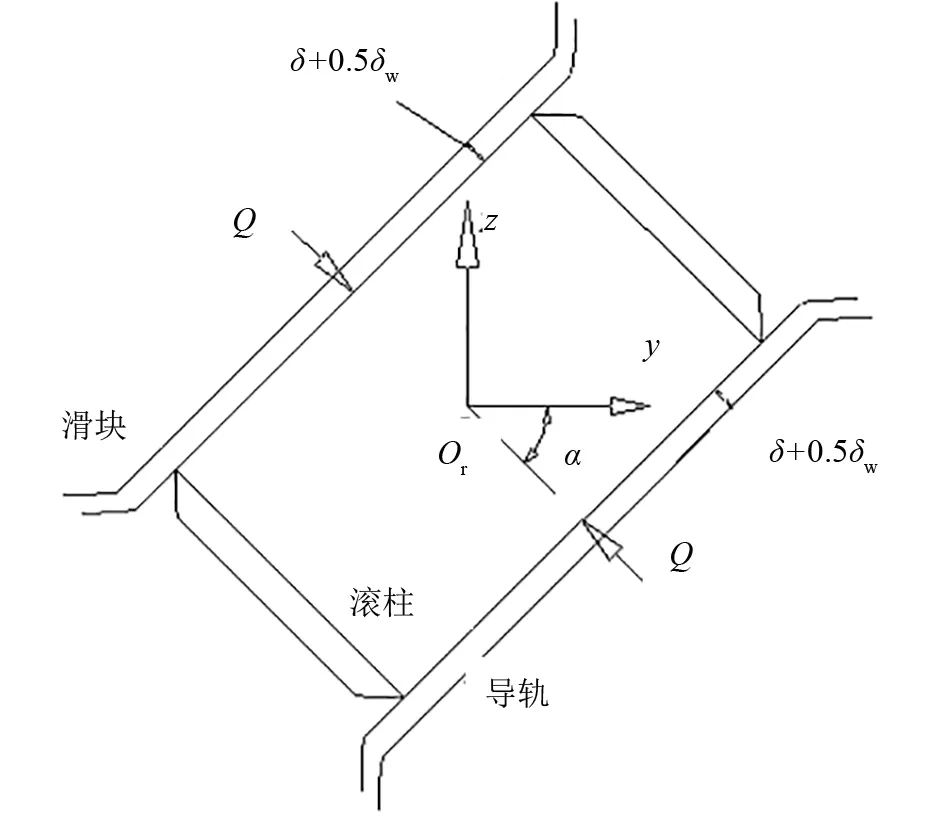
图2 滚柱与滚道接触变形

2 磨损导致滑块接触变形分析

如图3所示，设2个变形量δy，δz.

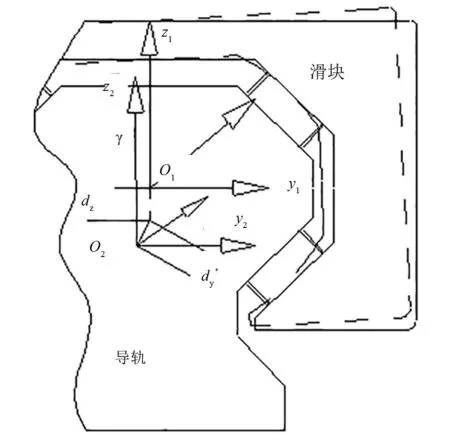
图3 滑块受载变形坐标系变化

滚柱导轨副的滑块在垂直外力的作用下，会同时产生纵向和横向的线性变形量(其中，由于沿X方向的轴向力主要由驱动滚珠丝杠承担，故认为X方向上不发生位移形变).在滑块几何中心建立坐标系，变形前和变形后的坐标系分别为O1，O2.

设δ0为初始预紧力Q0导致的滚柱初始变形量(双边变形量).滑块承受垂直外载荷时，由于预紧力的作用，上排滚柱综合变形为预紧力变形与外载荷变形的和减去磨损量的差值.下排滚柱的滑块为裙形结构，在预紧力作用下会产生扩张趋势.因此，下排滚柱的综合变形为预紧力变形减去磨损变形和外载荷变形的和.计算可得，上、下排滚柱的综合变形量为式(2).

(2)

3 垂直载荷滑块接触变形分析

当导轨副受垂直外载荷时，对滑块进行受力分析，建立滑块受力平衡方程.设n为单列同时承载的滚柱个数.由于滑块的对称性，上排2列滚柱变形一致，下2排滚柱变形一致.于是式(3)成立.如图4所示.

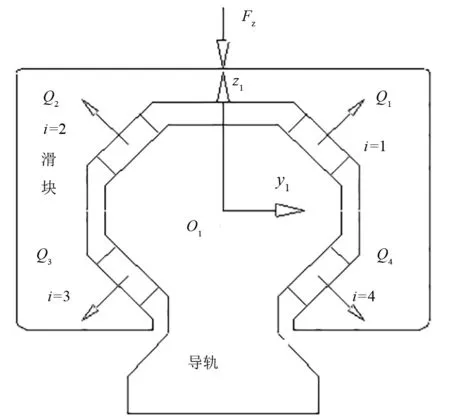
图4 滑块受力分析

(3)

4 磨损导致接触角变化分析

当滚柱导轨副滑块只承受垂直载荷时，随着垂直载荷的增加，上排滚柱受力增大而下排滚柱受力减小，上排滚柱通过增大接触角而起到抵消受载或者磨损的趋势，同时下排滚柱在预紧力的作用下产生导轨副的裙部外扩的趋势也随着外载荷和磨损的增加而产生变小的趋势.设上排滚柱初始接触角为α，磨损和受载综合作用后的接触角变为αw.α<αw.

根据上排滚柱双侧接触角状态图5可知：

(4)

化简可得变化后接触角的表达式：

(5)

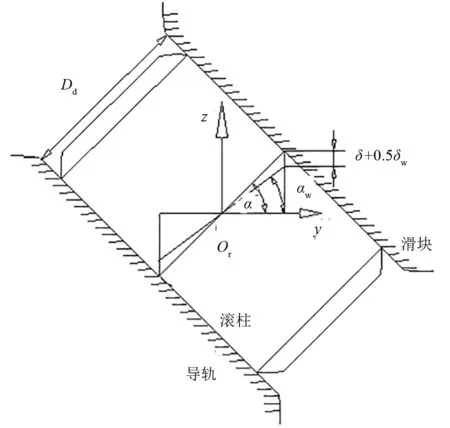
图5 滚柱接触角分析

由于预紧力的作用会使得滑块的裙部张开，在受到外载荷时裙部变形回缩，因此类似的，根据上排滚柱双侧接触角变化的分析可得到下排接触角具有与上排相同变化的规律.

5 接触角变化对Archard模型磨损体积的修正

如图6所示，为单个滚柱的受压截面图.

图6 磨损体积截面图

根据Archard磨损模型公式.

(6)

式中：△V/m3为滚道磨损体积；K为磨损系数；L为滚动磨损距离，m；P为外力载荷，N；PM为滚道材料硬度，N/m2.

结合公式(5)和公式(6)可得到磨损量导致接触角的变化对磨损体积的修正量.

(7)

6 磨损模型仿真

6.1导轨副相关参数

以某公司的LGR36型滚柱直线导轨副为研究对象，该型号导轨参数如表1所示.

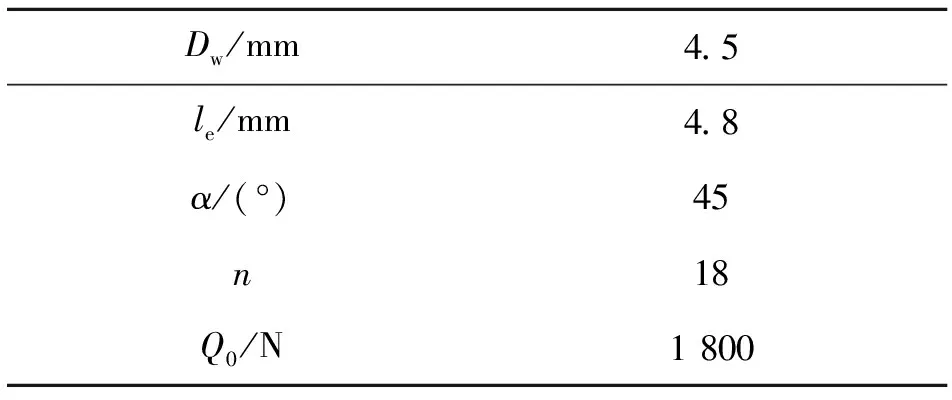
表1 LGR36型滚柱直线导轨副参数

6.2导轨副滚柱接触力计算

对于钢制导轨副，材料的弹性模量E=206 GPa，泊松比ν=0.3，因此，公式(1)可写为：

(8)

通过第一节公式仿真计算，可得滚柱接触力及外载荷之间的关系，如图7所示：

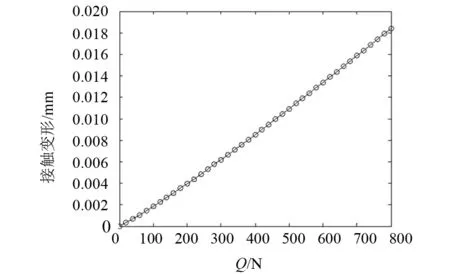
图7 接触力Q与滚道变形δ关系

6.3 滚道磨损量对接触角影响计算

通过第四节公式仿真计算，可得滚柱导轨副滚道的磨损与接触角之间的关系，如图8所示：

图8 磨损量对接触角的影响

6.4 滚道磨损量对滑块上、下排接触力的修正计算

通过第3节公式与第4节公式仿真计算，可得滚柱导轨副滚道的磨损量对滑块上、下排接触力修正的关系，如图9和图10所示.

图9 磨损量导致接触角变化对上排接触力的修正量

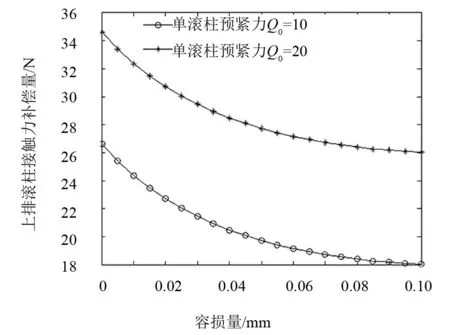
图10 磨损量导致接触角变化对下排接触力的修正量

6.5 滚道磨损量对滑块上、下排接触力的修正计算

通过第5节公式仿真计算，可得不同预紧等级下，滚柱导轨副磨损导致的接触角变化对磨损体积的修正关系，如图11所示.可得不同滑块受压下，滚柱导轨副磨损导致的接触角变化对磨损体积的修正关系，如图12所示.

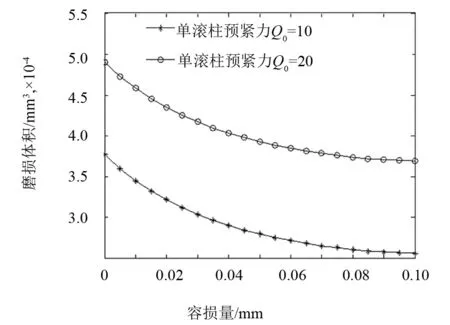
图11 不同预紧下磨损量导致接触角变化对磨损体积的修正量

7 分析与结论

从图7中可看出，滚柱导轨副中滚柱的接触力与滚道变形呈现趋于线性的变化关系.随着接触力的上升曲线微微呈现下凹.

从图8中可以看出随着磨损量的增加，滚柱的接触角逐渐变小.上、下排滚柱呈现同样的变化规律.从图8中可见随着磨损的发生接触角确实发生了微弱变化.在精密计算中不能被忽略.

从图9和图10中可以发现，随着磨损的发生接触角对上、下排的法向接触压力也有一定影响.随着磨损增加，上、下排法向接触力都呈现非线性变化趋势，磨损初期接触力变化较大，随着磨损的继续增加法向接触力的变化有减小趋势.上排法向接触力的变化量要比下排滚柱的大.

从图11和图12中可以发现，由于磨损量导致的接触角的变化对磨损体积有一定的影响，需要在计算磨损量时加以修正，从图中可以看出，磨损量较小时需要修正的磨损体积较大.磨损量达到一定值时，磨损体积的修正趋于一个很小的值，并保持平稳.相同外载荷下，单个滚柱预紧增加会使得磨损体积补偿量增加.单个滚柱预紧力不变，增加外载荷会使得磨损体积的补偿量增加.

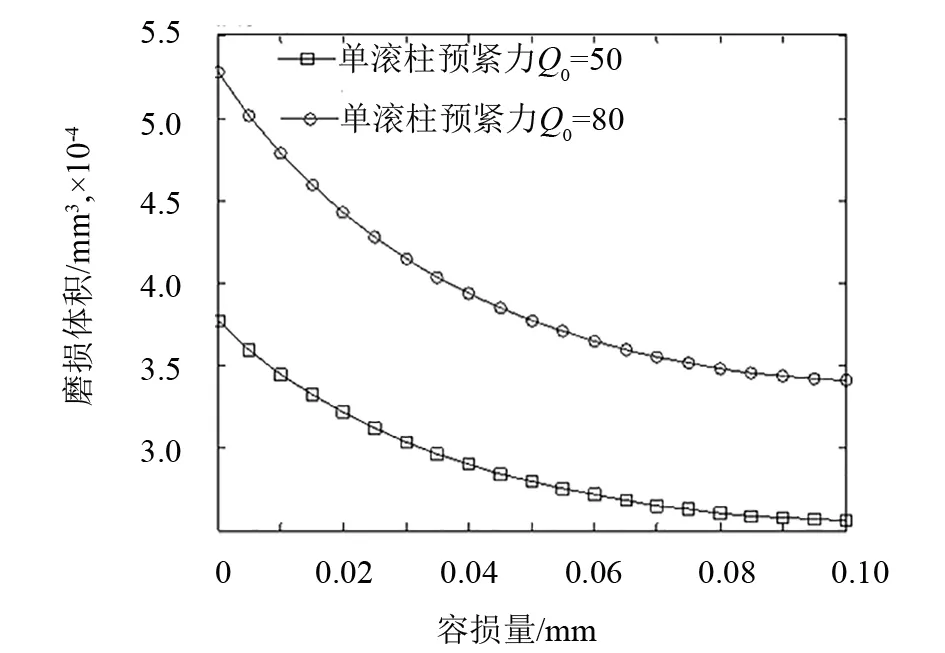
图12 不同受载下磨损量导致接触角变化对磨损体积的修正量

经过上述分析得出：1.考虑磨损量对接触角的变化对磨损模型的修正有一定的实际意义，为后续的滚动磨损分析打下了基础，可以在一定程度上揭示磨损初期磨损较为明显的现象.接触角的变化是导致磨损初期明显的原因之一.2.随着预紧力的丧失，上、下排的接触角变化趋于零，滑块受预紧力的裙部张开变形得以恢复，磨损体积的补偿量也趋于零，分析结果完全符合实际情况.证明了该模型的正确性.