小型风力发电机叶片损伤识别试验研究*
2022-08-04顾永强王晨
顾永强,王晨
(内蒙古科技大学 土木工程学院,内蒙古 包头 014010)
风力发电机叶片作为捕捉有效风能的主要部件,其正常运转是保证风电机组稳定运行和长远工作的关键原因[1].风电机组工作环境恶劣,在运行过程中会对叶片产生不同程度的损伤[2],影响风机正常工作,甚至产生安全问题,因此,对风机叶片损伤识别定位具有重要的工程应用价值.在目前众多的损伤识别方法中,结构的自振频率由于测量精度高、测量方法简单等优点,被广泛应用于机械、桥梁的损伤识别,但是无法对损伤位置进行定位.本文基于风力机叶片的实际工作情况,将其等效成悬臂梁结构,搭建了风机叶片模态测试实验平台,采集到了完整状态和3种损伤程度下叶片的振动响应信号,并运用自互功率谱法对振动信号进行处理分析,利用得到的完整状态和损伤状态下的模态参数对损伤程度和损伤位置进行了识别.
1 自互谱密度法
自互谱密度法是由峰值法演化而来的[3],该方法的主要思想是:由于输入信号是未知的,不能直接根据输入信号和输出信号直接得到结构的频率响应函数,因此通过数据采集到的信号,建立结构各点之间的自功率谱密度和互功率谱密度来表示频率响应函数[4],进而分析得到频率、振型、阻尼比等模态参数.
对实模态系统来说,由响应函数和激励函数xi(ω)关系可知,频率响应函数fk(ω)可表示为:
(1)
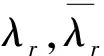
在结构激励无法测出的情况下,选择结构上某一响应点作为参考点,将这个参考点的输出响应作为其他响应点的输入,由于参考点与其他的响应点之间具有某种线性相关性,因此可建立参考点与响应点之间的传递函数,通过传递函数进行系统的模态识别[5].假设在结构上选取一固定点P作为参考点,则传递率可表示为:
(2)
假定环境激励是一个平直谱信号,且功率谱密度函数均匀覆盖于结构的所有模态,则可将其看作为一个常数C1,即可认为[6]:
fk(w)=f(ω)=C1.
(3)
对于结构的某一频率ω,序列αi(ω)就是其对应频率下的工作模态.结构上任何一点的动态位移响应xi(ω)都可以用k点的激励力fk(ω)和系统的传递函数hik表示:
(4)
式中:hi(ω)是集总频响函数.将式(4)代入到式(2)中可以得到:
(5)
由于P点是固定点,xp(ω)为P点的动态位移响应,对于一个确定的固有频率ωr=|λr|,Φpr是常数,因此式(5)又可表达为:
(6)
式中:C2是常数.
从上式可知,在固有频率ωr处的工作挠度曲线可以通过传递率曲线直接得到,可以近似的认为是结构的第r阶振型[7].
2 风机叶片振动试验
此次试验选择了玻璃钢材料的的小型叶片(1.5 m),通过振动数据采集器及采集分析软件(XL3308),万能试验机,力锤,压电式加速度传感器(YD81型),微型计算机,卷尺,电荷放大器(DHF-9双积分)等仪器,测定在力锤瞬时激励下加速度时程曲线图.
查阅相关文献[8,9],风力发电机叶片在工程事例中产生的损伤主要发生在根部,且以横向裂纹为主,针对此特点,本实验对叶片进行模拟裂缝损伤试验.对距离叶根40 cm叶片分别切割不同损伤面积的裂缝来模拟不同大小的损伤,叶片破坏后的工况如下表1所示,模型如图1所示.

表1 叶片损伤工况表

图1 距离叶根40 cm损伤叶片模型
布置试验装置时,将叶片尾部固定在万能试验机上,通过油泥将4个YD81压电加速度传感器逐个等距离安装在叶片表面上,从叶尖到叶根,传感器依次代表的是通道1,通道2,通道3和通道4,其距离为30 cm,其传感器安装情况如图2所示.

图2 传感器布置图
试验通过单点激励、多点采集的方法,得到叶片上不同测点在挥舞方向的振动响应情况[10].首先使用力锤敲击风力机叶片,振动产生的电信号经过压电式加速度传感器传递给动态数据采集器,采集分析软件进行进一步的处理和分析,得到其实验数据.
3 叶片模态参数辨识分析
通过XL3308动态数据采集器及采集分析软件,得到叶片在瞬时激励下的4个通道的自由振动信号,图3为实验瞬态激励所得到的4个通道加速度时程曲线图,设置信号所采用的采样频率为512 Hz,它可以较好的计算出200 Hz以下的频率.
对图3得到的4个通道时域数据进行预处理,抑制噪声对信号的影响.通过Matlab程序的数据处理,可得到4个传感器对应的的自功率谱图,以及互功率谱幅值相位图,传递率图以及相干函数图.
与自功率谱幅值相比,互功率谱对毛刺有一定的抑制作用[11],所以,工程实际中通常使用互功率谱进行结构的模态参数识别.参考通道与其他通道的互功率谱幅值图如图4所示,从图4可以初步得到各峰值对应的频率大约12,39.43,44.63 Hz.
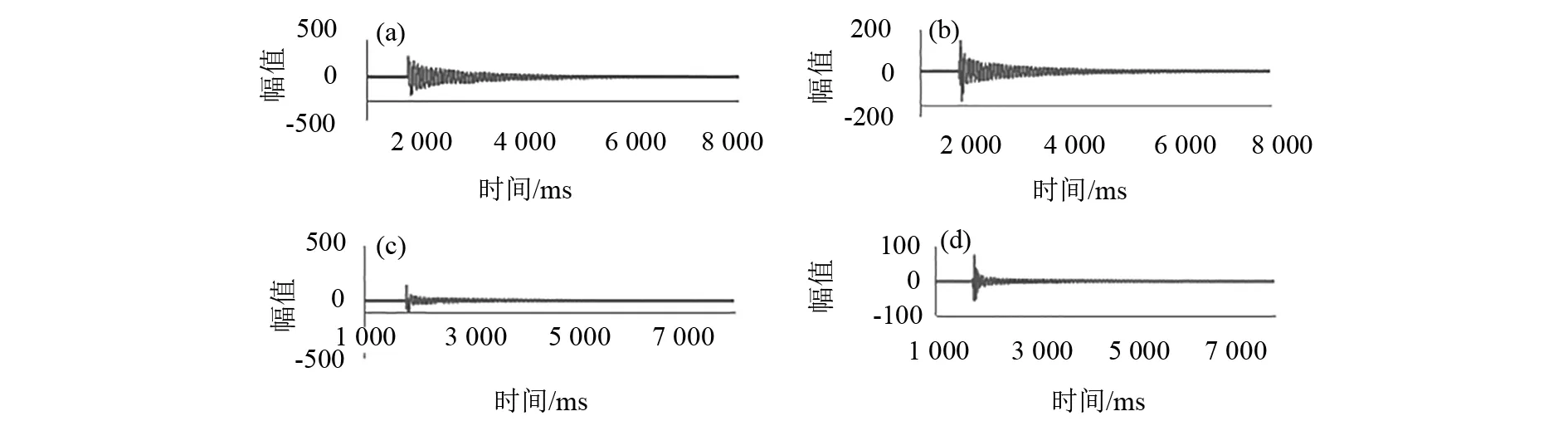
图3 力锤瞬时激励下加速度时程曲线图(a)通道1时域图;(b)通道2时域图;(c)通道4时域图;(d)通道4时域图

图4 参考通道与其他通道的互功率幅值图(a)1,2通道互功率谱幅值图;(b)1,3通道互功率谱幅值图;(c)1,4通道互功率谱幅值图
从互功率谱幅值图中,能初步得到结构的固有频率,但是由于噪声等因素产生的虚假模态(如毛刺),得到的固有频率不一定是真实频率,因此需要进一步通过互功率谱相位和相关函数进行判断.大量的工程结构表明,如果互功率谱幅值图中频率峰值,其对应的相干函数的相干性能值不低于0.95,且在该位置的互功率谱相位在0度或者180度(误差在正负30度以内),即可以认为该峰值频率就是叶片的真实固有频率值[12].
图5,6分别为参考通道与其他通道的互功率谱相位图和相干函数图,将前面得到的频率分别代入图5,6进行验证,判断这几个峰值频率的正确性,通过验证,得到叶片的一阶固有频率为12 Hz,二阶固有频率为44.63 Hz.

图5 参考通道与其他通道的互功率谱相位图(a)1,2通道互功率谱相位图;(b)1,3通道互功率谱相位图;(c)1,4通道互功率谱相位图

图6 参考通道与其他通道的相干函数图(a)1,2通道相干函数图;(b)1,3通道相干函数图;(c)1,4通道相干函数图
由前面介绍的理论可知,在进行振型识别时,振型的方向可以通过读取叶片固有频率在互功率谱相位或者传递率实部的值来确定,而振型的大小可以通过识别叶片固有频率在传递率曲线的值来确定.在确定各个传感器振型大小和方向后,采用归一化对振型幅值进行处理,利用曲线拟合出完整叶片的振型图.一般来说,叶片只需分析前两阶振型就能满足检测要求[13,14].叶片无损伤下一阶挥舞方向拟合曲线如图7所示,图7是工作挠度曲线,是叶片在外力下的相对变形,并不是严格意义上的振型.
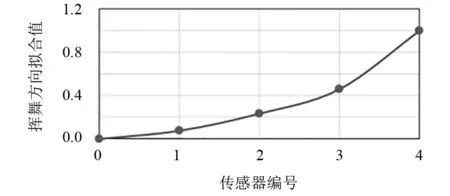
图7 叶片无损伤下一阶挥舞方向拟合曲线图
对损伤的叶片进行模态参数识别,可以得到不同工况下的频率和振型,其频率变化结果如表2所示.
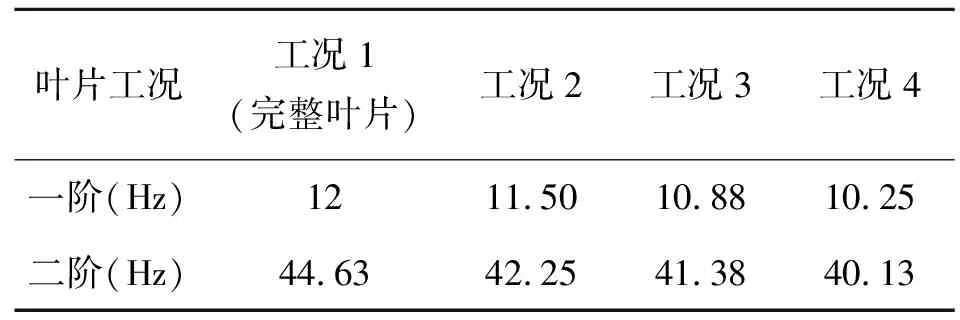
表2 损伤前后前两阶频率变化表
4 叶片损伤前后模态参数对比及分析
4.1 频率分析
由表2得,与完整叶片相比,在3种损伤程度下叶片的一阶、二阶频率都有下降.在工况2下一阶频率改变率为4.16%,随着损伤面积的增大,在工况4下一阶频率改变率达到14.58%,下降程度更多.此外,发生损伤后,一阶频率比二阶频率下降更加明显.其中工况4下二阶频率改变率仅有10.08%.因此可以通过固有频率的变化确定叶片是否发生损伤.
4.2 振型分析
结构位移模态振型变化率的表达式为:
(8)
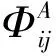
计算各位置处的一阶振型差变化率αij,并进行比较.图8为3种损伤程度下的一阶振型差变化率曲线图.由图8可知,裂纹所在位置与曲线峰值点相对应,当叶片某一局部出现裂纹时,其裂纹的周围区域模态振型与其他部分相比,振型差变化率明显大于其他无损伤位置,呈现凸起状,且随着损伤程度的增大,振型差变化率也增大,因此可以通过一阶振型差变化率对叶片损伤进行定位.
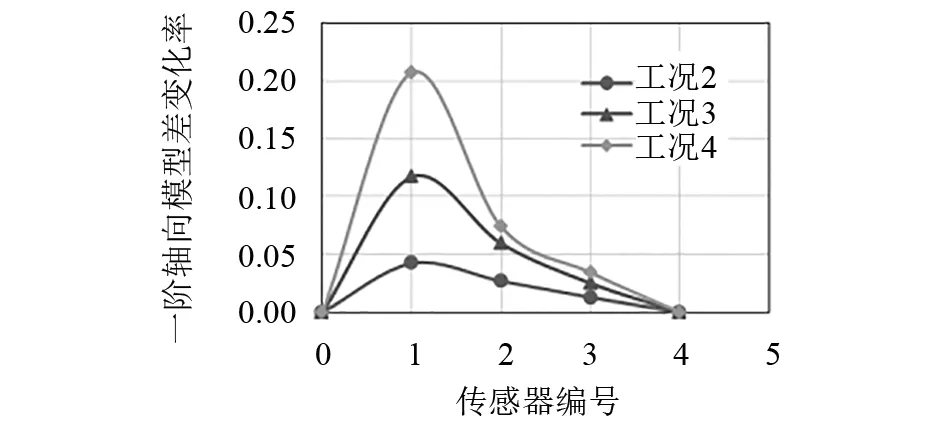
图8 3种损伤程度的一阶振型差变化率曲线图
5 结论
根据风力机叶片的实际工作情况,搭建了风机叶片模态测试实验平台,通过对比叶片损伤前后频率、振型,得出以下结论:
1)叶片发生损伤后,叶片的一阶、二阶频率都有降低,其中一阶频率比二阶频率下降更加明显,此外,随着损伤面积的增大,下降程度更多,所以可以通过各阶固有频率的下降作为判断叶片损伤的依据.
2)通过轴向振型差变化率曲线可知,叶片损伤周围区域模态振型与其他部分相比,变化更加明显,损伤所在位置与曲线峰值位置基本相吻合,表明轴向振型差变化率可以对叶片的损伤位置进行有效定位.
通过对叶片损伤的识别与定位,不仅能保证风力发电机安全稳定运行,还能优化叶片复合材料铺层,充分利用材料,具有重要的工程意义.
