考虑装配误差的行星滚柱丝杠副载荷分析与研究
2021-01-04刘柱范元勋
刘柱,范元勋
(南京理工大学 机械工程学院,江苏 南京 210094)
0 引言
行星滚柱丝杠主要由丝杠、滚柱和螺母3部分组成,具有将旋转运动转化为直线运动的特点[1]。相比行星滚珠丝杠,其具有更高的承载能力及使用寿命。行星滚柱丝杠在精密传动领域特别是航空航天领域已经得到了越来越多的关注和肯定[2-3]。
目前,国内外对于行星滚柱丝杠的理论研究已有一定基础,理论研究主要集中在运动学分析、轴向变形、动态特性以及传动效率等方面[4-7]。在螺纹牙载荷分布方面,杨家军等[8]依据Hertz 弹性接触理论,将滚柱作为整体,建立了刚度模型,得到了载荷分布与轴向刚度曲线;马尚君等[9-10]将滚动体等效成承受剪应力的矩形单元,建立了载荷分布计算模型,并与有限元解进行对比。上述研究为行星滚柱丝杠副的载荷分布研究奠定了理论基础,但均未考虑装配误差对滚柱两侧轴向分布的影响,且均假设各滚柱载荷分布相同,其对行星滚柱丝杠两侧载荷分布影响因素研究尚不充分。
本文根据行星滚柱丝杠副中螺纹牙两侧的变形协调关系,考虑装配误差对滚柱螺纹牙两侧产生的接触变形,建立了各滚柱的载荷分布计算模型,得出了各滚柱的载荷分布规律,分析了装配误差对行星滚柱丝杠中滚柱轴向载荷的影响规律。通过控制装配误差,有利于改善行星滚柱丝杠均载特性。
1 装配误差
行星滚柱丝杠是一种将旋转运动和直线运动相互转化的机构。其中滚柱、内齿圈和保持架等零件整合到圆螺母上,安装时直接将圆螺母沿着丝杠螺纹旋进就可以直接使用,如图1所示。

图1 行星滚柱丝杠结构
综合行星滚柱丝杠的结构形式和传动原理,行星滚柱丝杠在机构中的装配方法如图2所示。图2中,丝杠与驱动电机相连,通过螺纹副将动力传递给圆螺母,圆螺母则通过螺钉联接等方式与滑轨固连在一起作直线往复运动,轴承座和滑轨分别为丝杠和圆螺母起到定位的作用。
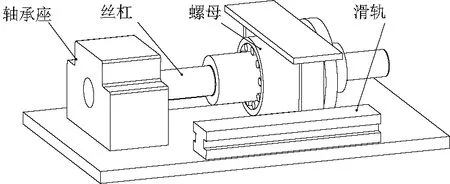
图2 行星滚柱丝杠装配方式
基于这种装配方式,行星滚柱丝杠的装配简图如图3所示。图3中,hs表示丝杠与轴承座配合后,其中心轴线与支撑平面的距离;hn表示与滑轨固连后,圆螺母中心轴线与支撑平面之间的距离。由于轴承座和滑轨竖直方向上尺寸误差的存在,致使丝杠与圆螺母在安装完成后二者的中心轴线在竖直方向上并不重合,因此hs≠hn。设t=hs-hn,当t>0时表示丝杠相对圆螺母向上偏移;t<0则表明丝杠相对圆螺母向下偏移。

图3 行星滚柱丝杠装配示意图
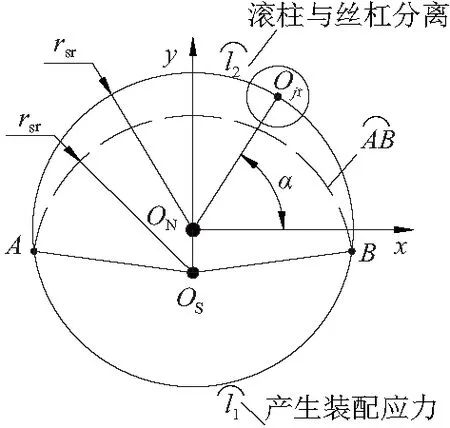
丝杠与滚柱中心距发生变化后,滚柱不再是均匀分布在丝杠四周,如图4所示。图4中,设滚柱与丝杠无装配误差时的中心距为rsr;滚柱个数为k。OS和ON分别表示丝杠和螺母的中心点;Ojr表示第j个滚柱的旋转中心;rjsr表示第j个滚柱与丝杠的中心距。根据三角形余弦定理可得:

图4 装配误差后滚柱与丝杠接触关系
(1)
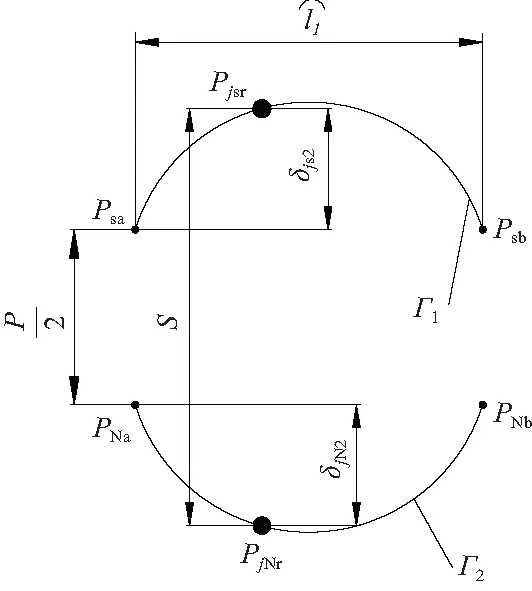
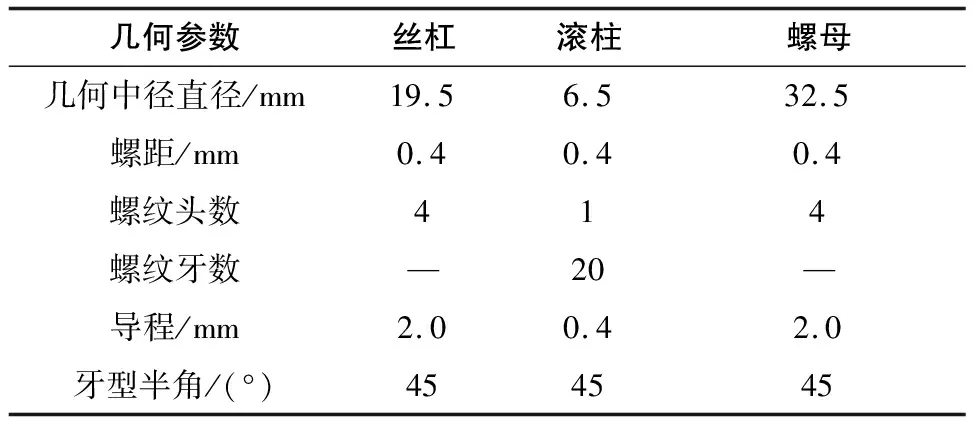
若rjsr 图5 与丝杠接触的滚柱范围 本文研究基于这样的假设,即所有弹性变形都在弹性范围内且不考虑丝杠轴段的弯曲变形,并且各滚柱两侧啮合点关于丝杠对称。装配应力会使行星滚柱丝杠在转动前螺纹牙就发生接触变形,且接触变形大小和滚柱与丝杠的中心距有关。设第j个滚柱丝杠侧因为装配应力产生的法向接触变形为δsj,将δsj正交分解为δsj1和δsj2。其中,δsj1为滚柱螺纹牙沿OS-Ojr方向的变形,δsj2表示滚柱轴向接触变形,β为接触变形δsj与δsj1的夹角,则 δsj2=δsj1·tanβ (2) 将丝杠和滚柱等效成圆柱体,半径为各自螺纹中径,滚柱丝杠侧各螺纹牙产生的接触变形为 δsj1=rsr-rjsr (3) 根据赫兹接触变形公式,第j个滚柱丝杠侧各螺纹牙由于装配误差产生的轴向载荷Fjsa如下: (4) 其中C为滚柱和丝杠的接触刚度。根据静力平衡条件,滚柱在螺母侧各螺纹牙接触变形δNj2与δsj2相等。 螺纹牙装配应力变形使得滚柱在丝杠和螺母两侧的啮合点在轴向方向产生位移,且第j个滚柱啮合点的轴向位移为δsj2。因为同一滚柱的螺纹牙接触变形相同,所以同侧相邻啮合点的轴向距离仍然为螺距P。滚柱两侧啮合点变化如图6所示。图6中,设A、B两点处的滚柱在丝杠和螺母两侧的啮合点Psa、Psb和PNa、PNb为参考点,曲线Γ1和Γ2分别为滚柱在丝杠和螺母侧的啮合点变化曲线。Pjsr和PjNr分别表示第j个滚柱丝杠和螺母两侧的啮合点。 图6 滚柱啮合位置变化曲线 设Pjs(i-1)和Pjs(i)为第j个滚柱与丝杠啮合的相邻两个接触点,假设丝杠在Pjs(i-1)Pjs(i)之间还有与其他z个滚柱的接触点。因此,Pjs(i-1)Pjs(i)被分成了z+1段,设每段的轴向内力为Fj,每段的距离为△Pi,所以丝杠在Pjs(i-1)Pjs(i)的轴向变形如下: (5) 滚柱和丝杠及螺母在电机施加轴向载荷时,以丝杠或螺母中任意相邻螺纹牙上的啮合点为研究对象,列出两个啮合点的变形协调方程: L+δi+1+ΔLsi=L+ΔLri+δi (6) 其中:L的长度等于螺距P;ΔLsi和ΔLri分别表示两啮合点间丝杠和滚柱的轴向变形。 第j个滚柱在丝杠和螺母两侧的总轴向力大小相等,得平衡方程: Fjs=Fjr (7) 丝杠轴向平衡方程: (8) 如图7所示,Faji表示第j个滚柱上与丝杠接触的第i个螺纹牙所受的轴向载荷,曲线为丝杠螺旋线。由图7可以得到多个滚柱的轴向变形物理方程如下: 图7 滚柱间轴向变形关系 (9) 通过联立式(5)-式(9),求出存在装配应力时电机施加载荷后每个滚柱两侧的载荷分布情况。 采用表1和表2中所列出的一组行星滚柱丝杠进行分析,滚柱个数为2,其额定承载能力为2 t。行星滚柱丝杠副中的丝杠、滚柱及螺母的材料为GCr15,弹性模量为2.12×1012,泊松比为0.29,装配误差t=0.5 mm。 表1 行星滚柱丝杠几何参数 表2 滚柱在圆螺母中的位置 通过matlab可计算出每个滚柱分别在丝杠与螺母两侧的螺纹牙载荷分布情况,计算结果如图8所示。由图8可知,滚柱2载荷为0,即滚柱1出现空载现象;滚柱1和滚柱3应为关于y轴对称,所以两侧的轴向载荷相等;滚柱4两侧的轴向载荷最大。 (a) 滚柱丝杠侧载荷分布情况 采用C3D8M实体网格对滚柱、丝杠和螺母进行划分。将丝杠和螺母上的接触面选择为接触副面,滚柱接触面为接触主面,因此滚柱网格划分的单元尺寸比丝杠和螺母要小[11]。行星滚柱丝杠在Abaqus中包含的六面体网格数量为4 065 429,具有9 685 012个节点,分析模型如图9所示。 图9 行星滚柱丝杠有限元载荷分析模型 边界条件设置如下:丝杠与电机相连接的端面选择完全固定约束,滚柱和螺母仅保留轴向移动自由度。模拟负载施加载荷在螺母端,建立与螺母端面耦合约束的参考点,在参考点上施加集中力。本次有限元分析分为3步,第1个分析步实现滚柱和丝杠及螺母螺旋曲面的精确接触;第2个分析步对丝杠施加移动距离0.5 mm,使行星滚柱丝杠副中产生装配应力;第3个分析步中施加螺母端的轴向载荷,数值为20 kN。有限元后处理模块求解出滚柱轴向载荷与matlab求解结果对比如图10所示。 由图10知,本文建立的考虑装配应力时的滚柱载荷计算方法与有限元方法结果吻合度较好。 图10 滚柱两侧载荷 1)建立了考虑装配误差影响的行星滚柱丝杠各滚柱两侧螺纹牙载荷分布计算方法。 2)通过算例分析表明,装配误差的存在会造成行星滚柱丝杠中与丝杠中心距过大的滚柱出现空载现象;参与啮合接触的滚柱两侧轴向载荷大小与滚柱和丝杠的中心距呈负相关,中心距越大,滚柱两侧载荷越小。 3)装配误差对滚柱两侧载荷分布影响不可忽略,在实际安装过程中,应提高其装配精度,减少各滚柱两侧载荷差异。
2 考虑装配应力滚柱载荷分布
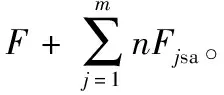

3 算例
3.1 算例


3.2 有限元验证


4 结语
