基于人工鱼群- 蚁群算法的UUV三维全局路径规划

胡致远， 王征， 杨洋， 尹洋

(海军工程大学 电气工程学院, 湖北 武汉 430033)

0 引言

水下无人航行器(UUV)具有体积小、机动能力强、智能化程度高、隐身性能好、作业风险低等特点，在海洋领域得以广泛应用。路径规划作为控制技术之一，能够保证UUV在具有障碍物环境的作业空间内，寻找到一条从起始点到目标点的最优路径。按照对环境的知晓程度，可以分为局部路径规划和全局路径规划。其中，全局路径规划适用于已知的海洋环境，为UUV的安全性和可靠性提供重要的支撑。

总体上看，路径规划算法可以分为传统算法和智能算法。相比于传统算法，智能算法具有简单、高效、适应性强、鲁棒性好等特点，被广泛应用于路径规划问题。应用较为广泛的有蚁群(ACO)算法、粒子群优化(PSO)算法、蜂群算法、人工鱼群算法(AFSA)等。除此之外，部分学者将萤火虫算法、烟花算法等用于路径规划问题，也得到了较好的研究成果。

ACO算法是意大利学者Dorigo等提出的一种新的模拟进化算法，是基于生物界群体启发行为的一种随机搜索寻优方法，在解决优化组合的问题上有良好的适应性，比较适合于求解三维路径规划问题。

围绕ACO算法的优化问题，文献[9]将告警信息素概念引入至ACO算法，减少了蚂蚁的无用搜索，提升了算法的整体收敛速度，但同时增加了算法的计算量；文献[10]将遗传算法的交叉操作结合到蚁群系统的路径寻优过程中，加强了蚁群系统的路径寻优能力；文献[11]将PSO算法与ACO算法相结合，利用PSO算法进行路径预搜索，优化了初始信息素配置，改善整体算法性能，但对于ACO算法的全局寻优能力缺乏考虑。

AFSA与ACO算法均属于智能仿生算法，在种群优化方面具有很多相似之处。围绕两者之间的融合问题，文献[12]计算了当前路径上的信息素和所有信息素累加和的比值，通过对比拥挤度因子与上述比值的关系，决定ACO算法是否依靠转移概率选取下一路径点。文献[13]在文献[12]的基础上，以AFSA搜索到的最优值更新ACO算法的初始信息素，解决了带时间窗的车辆路径问题。文献[14]中交替使用AFSA和ACO算法，不断地进行信息素更新和全局搜索，在解决工件数目较多的批调度问题时，具有较高的效率。因此对于两个算法的融合问题值得进一步研究。

本文采用栅格法对下载的真实海洋环境进行建模。考虑到传统ACO算法存在的初期搜索的盲目性、较为依赖初始信息素分布、易于陷入“早熟”等问题，将AFSA与ACO算法进行融合和改进，并通过仿真实验加以验证。

1 海洋环境获取和处理

1.1 海底地形获取

全局路径规划适用于已知的海洋环境。获取实际的海洋环境数据直接关系到UUV全局路径规划结果的有效性。

目前关于海底地形的数据库较多，数据的开源性便于用户根据需要下载对应的数据库数据。全球海陆数据库(GEBCO)包含2.9亿个海水深度的探测数据，数据精度能够满足路径规划研究的需要。

GEBCO提供了全球地图的显示插件，如图1所示。在插件上选取指定的海域框格，便可以下载对应的采样矩阵，用于后续的全局路径规划研究。

图1 GEBCO插件显示图Fig.1 GEBCO image

1.2 栅格法环境建模

目前针对环境建模方法主要包含栅格法、八叉树法和切线图环境表示法等。其中，栅格法建模具有操作简单、易于编程实现、与路径规划算法结合紧密等特点，能够将复杂的三维环境转换为计算机可以处理的数据文件。针对三维环境特点，采取等栅格平面法进行环境建模。

如图2所示，起始点和目标点之间的区域：-为路径规划区域，点位于平面，点位于平面。将点设为坐标原点，UUV的主航行方向设为轴，水平面内与轴垂直的方向设为轴，轴为深度方向，与水平面垂直。

沿轴方向，进行等距离切分，从而形成+1个垂直于轴并且平行于的栅格平面～+1。对任一平面沿着轴等分次，沿着轴方向等分次，从而在每个栅格平面中形成×个栅格。

为保证UUV航行的安全性，在每个栅格平面中，规定只要栅格中含有低于海洋深度或障碍物等情况的栅格均视为不可行栅格，图中用深色表示，其余栅格视为可行栅格，图中用浅色表示。

图2 栅格法建模示意图Fig.2 Schematic diagram of the grid model

通过栅格法建模后，三维路径规划问题可以转换为在多个垂直于主航行方向上的栅格平面中依次选取可行路径点～的问题。由于栅格平面沿轴方向均匀分布，因此研究中只需保存各路径点沿轴和轴方向的坐标信息，减小了计算机的存储量。各路径点之间连线形成的路径～便构成完整的三维路径。

1.3 搜索框设置

路径点搜索过程中，如果对下一栅格平面中的每个栅格点进行遍历搜索，将会导致搜索过程较为复杂，增加了算法的计算量。与此同时，UUV沿主航行方向航行时，受到其本身机动性限制，不可能在纵向和横向上有过大的位移，部分路径点将无法到达，失去研究意义。

综合考虑算法的计算成本和UUV的实际机动性能，进行搜索框设置如图3所示，进一步筛选可行路径点。搜索框由UUV的最大纵移距离和最大横移距离构成。当位于平面中的路径点搜索下一平面+1中的路径点+1时，只需要对搜索框中的可行路径点进行搜索即可。

图3 搜索框设置示意图Fig.3 Schematic diagram of the search box

2 融合算法设计

2.1 融合算法思路

ACO算法模拟自然界蚂蚁的觅食行为，通过信息素浓度的变化，指引蚂蚁寻找最优路径。ACO算法作为智能启发式搜索算法的一种，具有较强的适应性、鲁棒性、自组织性和分布式计算特性。但是，初始信息素的均匀分布使得算法初期具有一定的盲目性，算法的收敛速度因此降低。

AFSA是李晓磊博士于2002年提出的基于生物群体行为的智能算法。该算法模拟鱼群的觅食、聚群、追尾、随机等行为进行搜索寻优，具有简单、鲁棒性强、收敛速度快、初始参数选择不敏感等特点。因此，可以考虑将AFSA算法与ACO算法相结合，形成鱼群蚁群融合优化AFACO算法。

在算法初始阶段，利用AFSA进行路径预搜索，形成若干条可行路径。增加可行路径对应路径点的初始信息素分布，形成优化后的初始信息素分布。将优化后的初始信息素分布传递至ACO进行三维路径规划，从而降低ACO算法前期搜索的盲目性，提升整体算法的收敛速度。

2.2 融合算法流程

根据融合算法思路，制定算法流程，算法流程图如图4所示。主要步骤如下：

图4 融合算法流程图Fig.4 Flow chart of the fusion algorithm

1)使用GEBCO插件，下载路径规划研究所需的海域数据库，并进行环境地图的绘制；

2)设定起始点目标点信息，进行栅格法建模，确定划分的平面个数、栅格数量等；

3)设定AFSA相关参数，初始化人工鱼群分布；

4)分别以聚群和追尾为主要行为方式，穿插进行觅食和随机行为，形成新的人工鱼群分布，得到对应的食物浓度，根据食物浓度大小选择相应的鱼群分布；

5)若未达到鱼群算法最大迭代次数则继续循环，反之，增加当前鱼群对应路径点的初始信息素值，形成优化后的初始信息素分布；

6)设定ACO算法的相关参数，利用优化后的初始信息素，进行ACO算法的路径搜索；

7)计算路径适应度值，进行局部信息素和全局信息素更新；

8)判断是否达到了ACO算法的最大迭代次数。当达到最大迭代次数后，保存仿真结果，并进行结果的分析与处理。

3 AFSA的路径预搜索

3.1 基本的AFSA

人工鱼群的当前状态为，包含条人工鱼，则该状态下对应的食物浓度可以通过目标函数计算，并表示为：=()，在考虑路径长度最短问题时，目标函数即为路径的长度值。每条人工鱼的感知范围为，感知范围内其他人工鱼的数量为，移动步长为，拥挤度为。人工鱼与之间的距离,=‖-‖。

1)觅食行为

人工鱼在其感知范围内，随机选择另一状态，其对应的食物浓度若优于，则表明状态优于状态，人工鱼需要往该方向前进一步，状态更新为

(1)

如果并不优于，则重新随机选取状态进行比较。设置最大尝试次数为_。当尝试次数达到_时，若仍不满足觅食行为移动条件，则执行随机行为。

2)聚群行为

以人工鱼为中心，搜寻其感知范围内其他人工鱼的数量及中心位置。当>时，表明当前附近食物较为充足且不太拥挤，人工鱼向中心位置前进一步，否则执行觅食行为。状态更新公式为

(2)

3)追尾行为

以人工鱼为中心，搜寻其感知范围内其他人工鱼的数量及拥有最大食物浓度的人工鱼。当>时，表明当前附近食物较为充足且不太拥挤，人工鱼向前进一步，否则执行觅食行为。状态更新公式为

(3)

4)随机行为

人工鱼在感知范围内随机选取一个方向进行移动，状态更新公式为

=+*

(4)

3.2 AFSA设计

AFSA中，每一条人工鱼对应一种可行解，因此在三维路径规划问题中，可以将每条人工鱼视为一条可行路径。条人工鱼在第阶段的状态可表示为

(5)

由于起始点和目标点均已确定，即每条人工鱼表示的路径中起始点和目标点坐标固定不变。假设路径起始点坐标为(1,,)，目标点坐标为(+1,,)，人工鱼状态可以优化为

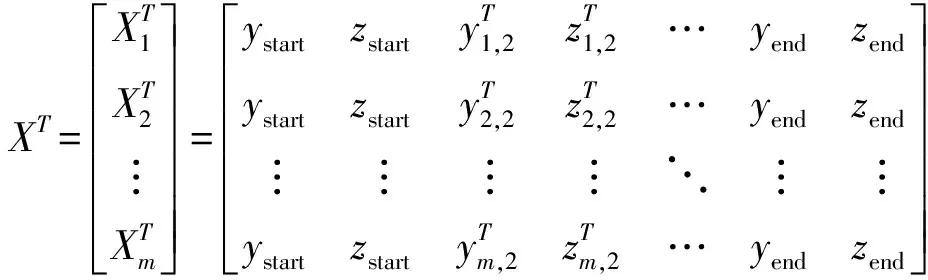
(6)

受到搜索框的限制，人工鱼的步长和最大横移距离和最大纵移距离存在的关系为

≤min (,)

(7)

4 ACO算法的路径规划

4.1 基本的ACO算法

传统ACO算法中，信息素通常分布在节点之间的连接上。对于三维路径规划问题，路径点即对应ACO算法的节点。由于路径点数量较多，节点之间的连接较为复杂，若将信息素存储于各路径点之间的连接上，势必增加了算法的空间复杂度。因此，考虑将信息素分布于各离散的路径点上，任意路径点对应一个信息素值。各路径点所包含信息素含量代表了对蚂蚁的吸引程度。

411 启发值大小

启发值关系到ACO算法的收敛性、稳定性以及求解的优化性。第个平面路径点，坐标(,,)到第+1个平面路径点+1，坐标(+1,+1,+1)的启发值,+1为

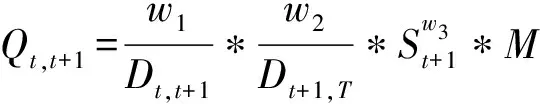
(8)

式中：、、为加权参数；,+1表示(,,)和(+1,+1,+1)之间的距离，计算公式为

(9)

+1,表示(+1,+1,+1)与目标点(,,)之间的距离，计算公式为

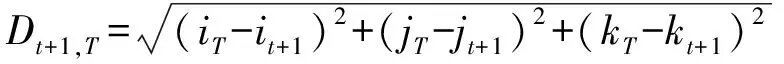
(10)

+1表示(+1,+1,+1)所在平面中可行路径点数量+1与总路径点数量的比值，

(11)

为路径深度方向变化值，通过相邻节点的深度坐标和+1进行计算，

(12)

按照实际求解问题，取1，取当前节点与目标点横坐标之间的差值，达到距离最短的设计原则；取正数，表示期望下一节点选择上要多考虑其可行性，保证UUV的航行安全。

412 转移概率

蚂蚁在路径搜索时，会依据路径点所含的启发值和信息素值计算转移概率。转移概率计算公式为

(13)

式中：+1表示路径点(+1,+1,+1)的信息素值；,+1表示两平面路径点之间的启发值；为信息素重要程度因子，其值越大，表示信息素在转移过程中作用越大；为启发值重要程度因子，其值越大，表示启发值在转移过程中作用越大。

413 信息素更新

为避免ACO算法陷入局部最优解，当蚂蚁搜寻到一个路径点或者寻找到一条可行路径后，需要进行信息素的局部更新和全局更新。

局部信息素更新目的是减小蚂蚁已通过节点的信息素值，增加未通过节点的被选择概率，实现全局搜索的目的。

局部信息素更新公式为

=(1-)

(14)

式中：为平面路径点的信息素；为局部信息素的衰减系数。

全局信息素更新在蚂蚁完成一条路径规划后，选择最佳路径，增加该路径上的信息素值，提高被选择的概率。信息素的局部更新和全局更新共同保证了ACO算法的成功搜索能力。

全局信息素更新公式为

=(1-)+Δ

(15)

(16)

式中：()为第只蚂蚁经过点路径长度；为全局信息素更新系数；为常量系数。

414 适应度函数

通过适应度函数判断路径规划结果的优劣程度。针对路径最短问题，当前路径的长度与适应度值密切相关。适应度函数设置为

(17)

式中：(path)表示路径path的总长度，可以通过累加相邻路径点坐标+1、的二范数求得。

4.2 改进ACO算法

ACO算法与AFSA具有一定的相似性：在不考虑信息素指导因素前提下，蚂蚁的搜索行为和AFSA中的觅食行为类似；蚂蚁优先选择信息素浓度高的路径与人工鱼的聚群和追尾行为类似。

但是，AFSA设置了拥挤度参数，在算法的初期可以避免个体过早地聚集到信息素较高的路径上，克服了“早熟”现象，提高了算法的全局寻优能力。

鉴于上述分析，将拥挤度因子思想引入传统ACO算法，将转移概率更新为

(18)

式中：+1表示当前选择的路径点拥挤度约束系数，根据路径点所含信息素浓度大小进行设定。假设+1平面中所有路径点所含的最大信息素浓度为，借鉴文献[12]中的思想，将拥挤度约束系数设置为

(19)

传统ACO算法路径点选取依照转移概率，按照轮盘赌的方法进行选择。由于各路径点之间的转移概率相差不大，如果依照轮盘赌的方法选择下一节点，不一定能完全保证具有较优转移概率的节点被选取。因此选取的路径点+1：

(20)

考虑到融合算法已经优化了初始信息素分布，因此在算法前期全局信息素更新系数选取较小的值，从而保证蚂蚁主要依靠初始信息素寻找路径；算法中期选取较大的值，避免信息素的堆积，增强算法的全局搜索能力；算法后期，由于较优路径基本搜索完毕，为了避免算法后期发散，选取较小的值。假设算法的最大迭代次数为，参考文献[21]，将的大小选取如下：

(21)

5 仿真结果分析

5.1 仿真实验环境

从GEBCO下载经度122.85°E～123.10°E，纬度24.15°N～24.40°N的海域数据集，数据沿经度和纬度方向每隔1 km采样，采样矩阵大小为30×30，UUV的主航行方向为沿经度方向。利用MATLAB软件对采样矩阵处理后，可以绘制采样的三维海洋环境，绘制出的海底地形图如图5所示。

图5 三维海底环境图Fig.5 Three-dimension submarine environment

依照栅格法建模，将研究海域沿经度方向切分30个栅格平面，并将起始点设置在第一个平面，目标点设置在最后一个平面。

仿真平台配置为Windows 7系统，Intel Core i5处理器，8 GB内存，算法利用MATLAB 2017A编程实现。

5.2 相关仿真结果

仿真中需要对算法相关参数进行设置。依据仿真实验环境设定，将栅格法参数设置记录于表1中。参照文献[12]和文献[16]中，关于AFSA和ACO算法的参数设置，将算法对应的参数列于表2和表3中。

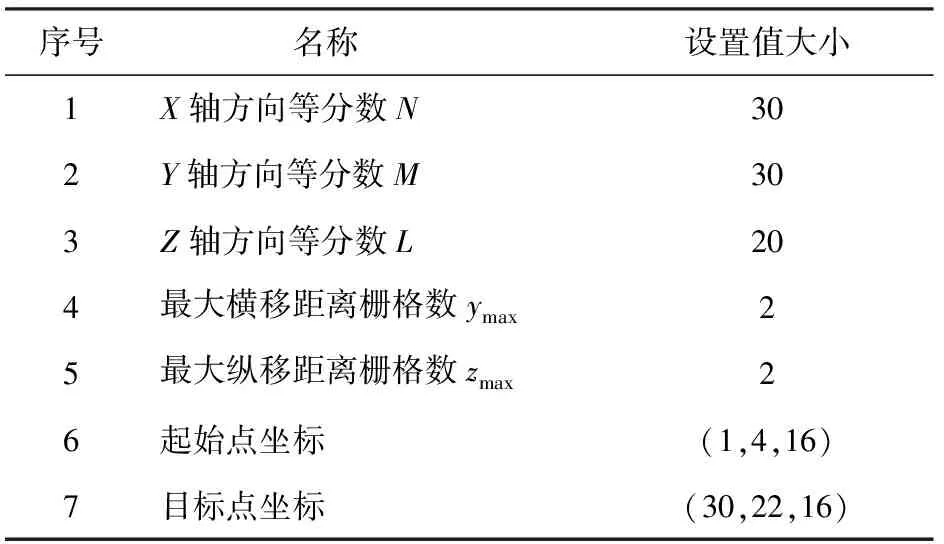
表1 栅格法参数设置

表2 AFSA部分参数设置

表3 ACO算法部分参数设置

按照融合算法的流程及参数设置，进行MATLAB编程仿真，经过AFSA预处理后结果如图6所示。

图6 AFSA预处理结果图Fig.6 Preprocessed results after AFSA

增加已搜索到的可行路径上路径点的信息素量，形成优化后的初始信息素分布。将优化后的初始信息素分布传递至ACO算法，进行仿真实验。为验证算法的有效性，在仿真中进行传统ACO算法、PSO算法和本文融合(AFACO)算法的对比实验。所得路径规划结果图、路径俯视图及适应度值变化趋势图如图7～图9所示。

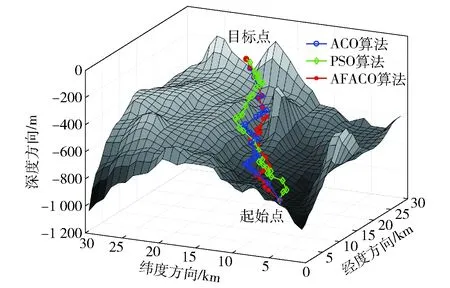
图7 路径规划结果图Fig.7 Path planning results

图8 路径结果俯视图Fig.8 Top view of path planning results

图9 适应度值变化趋势图Fig.9 Variation trend of fitness value

传统ACO算法在270次迭代时，达到最佳适应度值为41.398 1，PSO算法在267次迭代时，达到最佳适应度值为40.730 6，而本文融合算法在174次迭代时，达到最佳适应度值为40.033 8。

对算法连续仿真10次，将所得仿真结果的平均值记录于表4中。

表4 仿真结果(平均值)

5.3 仿真结果分析

从图6中可以看出，通过AFSA的预搜索，部分可行路径已经被找到，能够为初始信息素分布提供参考。

图7和图8表明传统ACO算法、PSO算法及本文的AFACO算法均能实现UUV的三维路径规划。结合图9的对比可以得到以下结论：

1)相比于传统ACO算法，AFACO算法和PSO算法在迭代初期的适应度值曲线能够较快的收敛，收敛速度较快；

2)与PSO算法不同，AFACO算法在算法后期仍具有较强的局部寻优能力，能够找到具有较优适应度值的路径，即具有较优路径长度的路径。

为了避免算法随机性带来的误差，表4计算了连续10次仿真结果的平均值。可以看出，AFACO算法在达到最小迭代次数时的耗时最小，与此同时，在最佳适应度值和最小迭代次数方面，较传统ACO算法及PSO算法均有一定的提升。

6 结论

本文充分利用了AFSA和ACO算法的特点，进行了人工鱼群- 蚁群融合算法的深入研究。通过对三维海洋环境的建模、融合算法的设计、ACO算法的改进等实现了UUV的三维路径规划。仿真结果表明，融合算法能够在保证获取最优路径的前提下，使用较少的迭代次数，收敛速度更快，算法的有效性得以验证。

[1] 钟宏伟.国外无人水下航行器装备与技术现状及展望[J].水下无人系统学报, 2017, 25(3): 215-225.

ZHONG H W. Review and prospect of equipment and techniques for unmanned undersea vehicle in foreign countries[J]. Journal of Unmanned Undersea Systems, 2017, 25(3): 215-225. (in Chinese)

[2] 严浙平,赵玉飞,陈涛,等.一种基于导航误差空间的无人水下航行器路径规划方法[J].兵工学报, 2014, 35(8): 1243-1250.

YAN Z P, ZHAO Y F, CHEN T, et al. A novel method of uuv path planning based on navigation error space [J]. Acta Armamentarii, 2014, 35(8): 1243-1250. (in Chinese)

[3] 曹晓明,魏勇,衡辉,等. 海流扰动下无人水下航行器的动态面反演轨迹跟踪控制[J].系统工程与电子技术, 2021, 43(6): 1664-1672.

CAO X M, WEI Y, HENG H, et al. Dynamic surface backstepping trajectory tracking control of unmanned underwater vehicles with ocean current disturbances[J]. Systems Engineering and Electronic, 2021, 43(6): 1664-1672. (in Chinese)

[4] AGHABABA M P, AMROLLAHI M H, BORJKHANI M. Application of GA, PSO, and ACO algorithms to path planning of autonomous underwater vehicles[J]. Journal of Marine Science and Application, 2012, 11(3): 378-386.

[5] 杜映峰, 陈万米, 范彬彬. 群智能算法在路径规划中的研究及应用[J]. 电子测量技术, 2016, 39(11): 65-70.

DU Y F, CHEN W M, FAN B B. Research and application of swarm intelligence algorithm in path planning[J]. Electronic Measurement Technology, 2016, 39(11): 65-70. (in Chinese)

[6] PANDEY P, SHUKLA A, TIWARI R. Three-dimensional path planning for unmanned aerial vehicles using glowworm swarm optimization algorithm[J]. International Journal of System Assurance Engineering and Management, 2018, 9(4): 836-852.

[7] 马焱,肖玉杰,陈轶,等.基于改进烟花- 蚁群算法的海流环境下水下无人潜航器的避障路径规划[J].导航与控制, 2019, 18(1): 51-59.

MA Y, XIAO Y J, CHEN Y, et al. Obstacle avoidance path planning of unmanned underwater vehicle in ocean current environment based on improved fireworks-ant colony algorithm[J]. Navigation and Control, 2019, 18(1): 51-59. (in Chinese)

[8] PU X, XIONG C, JI L, et al. 3D path planning for a robot based on improved ant colony algorithm[J/OL]. Evolutionary Intelligence, 2020(2020-04-13) [2021-03-30]. https:∥link.springer.com/article/10.1007/s12065-020-00397-6.

[9] MA Y N, GONG Y J, XIAO C F, et al. Path planning for autonomous underwater vehicles: An ant colony algorithm incorporating alarm pheromone[J]. IEEE Transactions on Vehicular Technology, 2018, 68(1): 141-154.

[10] 潘昕,吴旭升,侯新国,等.基于遗传蚂蚁混合算法的AUV全局路径规划[J].华中科技大学学报(自然科学版), 2017, 45(5): 45-49，76.

PAN X, WU X S, HOU X G, et al. Global path planning based on genetic-ant hybrid algorithm for AUV[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2017, 45(5): 45-49，76. (in Chinese)

[11] 朱佳莹, 高茂庭. 融合粒子群与改进蚁群算法的AUV路径规划算法[J].计算机工程与应用, 2021, 57(6): 267-273.

ZHU J Y, GAO M T. AUV path planning based on particle swarm optimization and improved ant colony optimization[J]. Computer Engineering and Applications, 2021, 57(6): 267-273. (in Chinese)

[12] 修春波, 张雨虹. 基于蚁群与鱼群的混合优化算法[J].计算机工程, 2008, (14): 206-207，218.

XIU C B, ZHANG Y H. Hybrid optimization algorithm based on ant colony and fish school[J]. Computer Engineering, 2008, (14): 206-207，218. (in Chinese)

[13] 邹挺. 基于蚁群和人工鱼群混合群智能算法在物流配送路径优化问题中的应用研究[D]. 苏州：苏州大学, 2011.

ZOU T. A study on the issue of vehicle route optimization upon ant colony algorithm, artificial fish swarm algorithm and hybrid swarm intelligence algorithm[D]. Suzhou：Soochow University, 2011. (in Chinese)

[14] 吕顺风. 蚁群鱼群混合算法在差异工件批调度中的应用[D].合肥：中国科学技术大学, 2017.

LÜ S F. Application of hybrid algorithms based on ant colony optimization and artificial fish swarm for batch processing machine with non-identical job sizes[D]. Hefei: University of Science and Technology of China, 2017. (in Chinese)

[15] MAYER L, JAKOBSSON M, ALLEN G, et al. The nippon foundation-GEBCO seabed 2030 project: The quest to see the world’s oceans completely mapped by 2030[J]. Geosciences, 2018, 8(2):63.

[16] 刘利强, 于飞, 戴运桃. 基于蚁群算法的水下潜器三维空间路径规划[J]. 系统仿真学报, 2008, 20(14): 3712-3716.

LIU L Q, YU F, DAI Y T. Path planning of underwater vehicle in 3D space based on ant colony algorithm[J]. Journal of System Simulation, 2008, 20(14): 3712-3716. (in Chinese)

[17] 丑强. 虚拟环境中基于八叉树的碰撞检测问题[D].长春：吉林大学, 2007.

CHOU Q. Collision detection in virtual environment based on octree[D]. Changchun：Jilin University, 2007. (in Chinese)

[18] 王磊. 海洋环境下水下机器人快速路径规划研究[D].哈尔滨：哈尔滨工程大学, 2007.

WANG L. Research on fast path planning for AUV in ocean environment[D]. Harbin: Harbin Engineering University, 2007. (in Chinese)

[19] DORIGO M, DI CARO G, GAMBARDELLA L M. Ant algorithms for discrete optimization[J]. Artificial Life, 1999, 5(2): 137-172.

[20] 李晓磊. 一种新型的智能优化方法- 人工鱼群算法[D]. 杭州：浙江大学, 2003.

LI X L. A new intelligent optimization method-artificial fish school algorithm[D]. Hangzhou：Zhejiang University, 2003. (in Chinese)

[21] 陈雄, 袁杨. 一种机器人路径规划的蚁群算法[J]. 系统工程与电子技术, 2008, 30(5): 952-955.

CHEN X, YUAN Y. Novel ant colony optimization algorithm for robot path planning[J]. Systems Engineering and Electronics, 2008, 30(5): 952-955. (in Chinese)