启发式搜索算法进行乐曲编辑的基本原理分析

戴幸

摘 要：该论文通过对启发式搜索算法进行乐曲编辑的基本原理进行分析，并对该算法实施乐曲编辑的主要步骤进行明确，最后，基于启发式搜索算法背景，对交互式计算机乐曲编辑系统进行乐曲编辑展开具体的实验与分析，重点解决的问题是搜索空间的限制、乐曲编码方法、确定评价函数。

關键词：乐曲编辑；启发式搜索算法；遗传算法；适应度；进化

一、启发式搜索的提出

启发式搜索算法是在状态空间搜索概念的基础上提出的。所谓状态空间搜索即针对某一个问题的求解的过程可以归纳为由问题初始的状态向目标状态转移并寻求路径的过程。归根到底，状态空间搜索即是两个不同状态中间的路径求解，其中不同点表现出来的为结果，路径所体现的则是过程；在很多情况下，一个问题的路径求解可能面临较大的分支，即部分求解条件存在一定的不确定性，这就使得求解的路径并非只有一条，从而构成了一副状态空间图，那么从状态空间图中寻找一个从初始到最终目标的路径过程便叫做状态空间搜索。

在绝大多数的状态空间搜索中，属于广度优先搜索或深度优先搜索，广度优先搜索是根据一定的顺序进行某一分支的搜索，该分支搜索完成之后再进行后续分支的搜索，最终以搜索到目标为结束标志。深度优先搜索则是按照层次从初始的状态逐层搜索，最终以搜索到目标为结束标志。

二、启发式搜索算法的基本原理

启发式搜索算法同样是以状态空间为基础的搜索方式之一，它的典型特征是预先对需要搜索的任何一个空间位置进行评估，从中筛选出最好的空间位置，然后按照这个位置作为搜索点展开新的搜索，直到寻找到最终的目标。利用启发式搜索算法能够有效避免无效的空间路径搜索，从而提升了搜索的效率。很明显，在启发式搜索算法中，对于空间位置的评估是非常重要的。当使用不同的评估策略时，获得的评估结果也是完全不同的。

一般情况下，启发式搜索算法的评估采取评估函数来表示，典型的如f（n） = g（n） + h（n），上述评估函数中，f（n）代表每一个位置n的评估函数，g（n）则代表了整个状态空间中从初始状态位置到n位置的真实代价，h（n）则代表了从位置n到目标位置的最优路径的代价。在评估函数中，h（n）是整个算法启发特征的表现，而g（n）函数是已知的，它主要表征了状态搜索的广度优先优势，当h（n） >> g（n）成立时，g（n）完全能够省略，从而有效提升了搜索效率。

当前，常见的启发式搜索算法包括有模拟退火算法、蚁群算法、人工神经网络和遗传算法。其中遗传算法作为来源于生物学领域进化论观点的一种算法，在搜索过程中可实现一定的并行性，整个搜索过程较为简单，可扩展性较强，具有良好的适应性，从而成为了启发式搜索算法中影响和应用最为广泛的算法。

三、乐曲编辑的遗传算法基本步骤

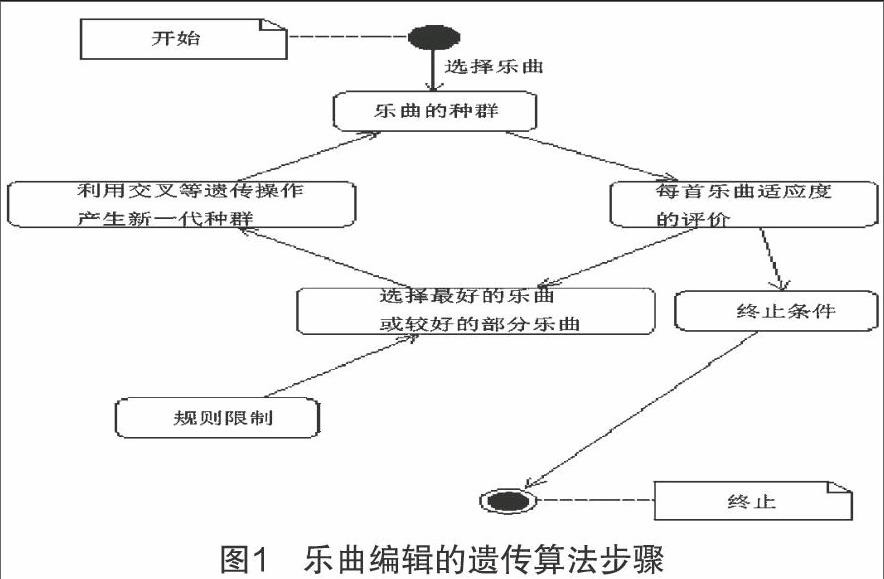
从遗传算法的本质来看，它具有典型的迭代特点。结合遗传算法的基本操作流程，可以获得乐曲编辑的遗传算法步骤。利用活动图，得到如图1所示的步骤：

上述步骤可以归纳为以下几个核心的过程：

（1）进行编码策略的选择，需要将域与乐曲的集合进行转换，结果为状态空间S；

（2）构建种群适应度评价函数；

（3）设置遗传策略，核心的操作主要包括有种群大小的确定，遗传操作（选择、交叉与变异）的具体方法，同时对遗传操作方法的各类概率参数进行确定；

（4）初始化种群；

（5）进行种群各位串解码后的适应度计算；

（6）根据遗传策略，多次重复进行遗传操作，判断新种群的性能是否达到既定的指标或者是否进行了足够的迭代次数。

四、乐曲编辑的遗传操作

在遗传算法中，进行乐曲编辑的遗传操作是在初始种群确定以及编码策略选择的基础上展开的，主要的遗传操作包含两种，一为交叉操作，二为变异操作。

交叉操作主要是以一定的交叉算子为基础进行，其根本的目标是在已经选择的种群个体中，通过两个不同位置个体的相同位置基因实施交换，以此来产生新的个体。在本次遗传算法的乐曲编辑中，交叉操作主要以单点交叉与两点交叉两种方式来展开。交叉操作执行之后 ，乐曲种群中将会产生更为优秀的种群个体，并进入到新的种群中。

五、结语

通过对启发式搜索算法进行乐曲编辑的基本原理分析，发现到目前为止，发达国家的一些研究人员针对计算机算法的乐曲编辑方式取得了不错的进展，一些基于算法的乐曲编辑系统也已经出现，典型的如Cybernetic Composer系统、CHORAL系统、EMI系统、ERNN系统、GenJam系统等，这些系统在一定程度上提升了乐曲制作过程中的人机交互能力。在国内，计算机算法乐曲编辑方面的研究绝大多数是基于理论的，具体的实践系统方面较少，这和国外相比具有较大的差距，需要在未来的研究过程中继续深入和完善。

参考文献：

[1]冯寅，周昌乐.算法作曲的研究进展[J].软件学报，2006，（02）：52-53.

[2]肖武雄.频谱音乐的曲式原则[J].星海音乐学院学报，2012，（04）：77-78.

[3]曹西征等.基于音高旋律元的柔和乐曲的自动作曲算法[J].自动化报，2012（10）：29-30.