自旋火箭弹横滚隔离系统的自抗扰控制

宋金超， 赵良玉

(北京理工大学 宇航学院, 北京 100081)

0 引言

自旋火箭弹是指弹体在飞行过程中绕其纵轴连续滚转的一类火箭武器，通常具有大长细比、多管(箱)发射、类抛物线飞行等特点。自旋体制具有简化控制系统组成，拓宽加工制造误差容限，提高突防能力，降低成本并提高打击效能等优势，得到了俄罗斯等军事强国的广泛关注和大力发展。然而，自旋火箭弹也存在一些特殊的动力学现象和制导控制问题，如一直困扰自旋火箭弹研制的锥形运动失稳等。随着信息化和智能化作战模式的来临，火箭武器也进入了全程制导的精确打击时代。为了进一步拓展作战任务范围和打击目标类型，对制导火箭弹提出了大机动、大落速、大落角等技术要求，这直接导致了用于自旋火箭弹惯性导航的横滚隔离系统，在大俯仰角(ϑ≥70°)情况下出现滚转陀螺超量程从而显著降低导航精度的现象，也使得大俯仰角飞行情况下自旋火箭弹横滚隔离系统的有效控制成了亟待解决的难题。

由于自旋火箭弹的低成本要求及弹体连续滚转的特点，使得其惯性导航系统广泛采用横滚隔离平台的形式以实现滚转通道的解耦。1986年，Imbault等在三轴稳定平台的基础上，取消方位稳定轴和俯仰稳定轴，只保留滚转通道的稳定回路以隔离弹体连续旋转，使惯性导航系统相对于惯性空间基本不转或者仅以很低的角速度滚转，故被称为横滚隔离平台。横滚隔离平台一方面隔离了弹体自旋，从而使滚转测量装置不受弹体自旋的影响，大幅度减小火箭弹对滚转陀螺的量程需求；另一方面大幅度减小滚转陀螺标度因数误差造成的导航误差，并提高系统的可观测性。针对横滚隔离平台的抗干扰及有效控制问题，国内外学者进行了广泛关注与研究。周琪等着重研究了隔离稳定回路的校正方案，通过采用超前滞后校正网络，对横滚隔离光纤捷联惯导稳定回路进行了优化设计，并在此基础上通过引入Stribeck模型模拟稳定回路摩擦力矩的非线性特性，建立了二阶离散自抗扰控制算法，有效地抑制了平台基座干扰。石永生等在横滚隔离的基础上，提出了静止基座捷联惯导系统(SINS)的两位置初始对准方案，通过改变绕旋转轴的惯性测量单元(IMU)侧倾角来提高可观测性，并且使对准误差最小。刘一鸣等针对恶劣弹载环境下，因滑环在传输过程中引入电气噪声而产生误差的情况，设计了一种采用伺服电机主动减旋的控制方法。2020年，宋金超等首次观测到大俯仰角条件下的横滚隔离平台失控现象，在建立自旋火箭弹横滚隔离系统数学模型的基础上，揭示了其失效机理，并通过设计该系统的比例- 积分(PI)控制器使其在阶跃扰动情况下能够正常工作。

进一步研究发现，自旋火箭弹在大俯仰角飞行情况下，若横滚隔离系统遭遇斜坡或正弦形式的扰动，其在PI控制器作用下仍然会出现滚转陀螺超量程并致其滚转隔离失效的现象。为此，本文在建立横滚隔离系统数学模型的基础上，通过理论分析和数值仿真揭示了PI控制器无法保证滚转隔离有效的机理，进而设计了一种自抗扰控制器，通过理论分析和数值仿真证明了该控制器可有效应对斜坡和正弦形式的扰动。

1 横滚隔离系统失效问题

1.1 横滚隔离系统控制原理

如图1所示，自旋火箭弹的横滚隔离控制系统主要由控制器、转矩电机、横滚隔离平台和捷联惯导系统构成。将传统的捷联惯导系统安装在横滚隔离平台上，即组成了横滚隔离二维捷联惯导装置。

图1 横滚隔离系统的物理组成示意图Fig.1 Schematic diagram of the roll-isolated system

为了满足初始对准和提高导航解算精度等工程实用化要求，横滚隔离系统的控制器通常仅将横滚隔离平台滚转角作为反馈输入量，控制目标是使该滚转角处于0附近，从而保证捷联惯导元件能够在不受弹体自旋的影响下工作。当因飞行状态变化导致横滚隔离系统受到扰动，原有运动平衡遭到破坏使平台滚转角不再为0时，通过反馈通道输入控制器的控制指令便不再为0，并使转矩电机向滚转角增量的反方向工作，直至消除扰动带来的滚转角变化。从控制系统的物理组成来说，可以将横滚隔离系统看作一类控制输入恒为0，而通过反馈量产生控制指令的特殊控制系统。

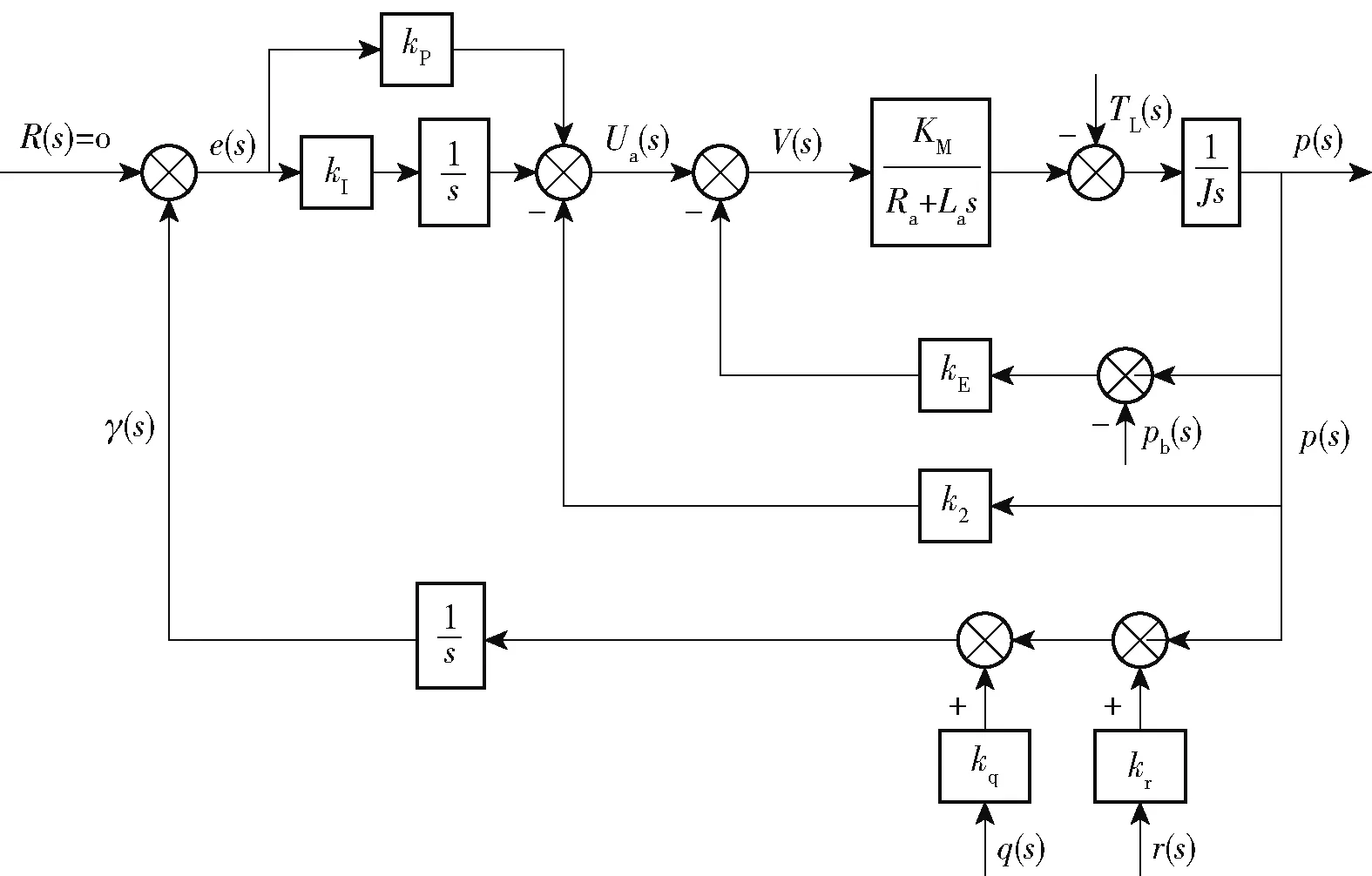
图2 采用PI控制器的横滚隔离系统结构图Fig.2 Schematic diagram of the roll-isolated system with PI control

1.2 斜坡和正弦输入的系统失效问题

以参考文献[16]采用PI控制器的横滚隔离系统为例，其结构如图2所示，四个扰动项分别为转矩电机负载(摩擦力矩等)()、弹体滚转角速度(与转矩电机定子转速相等)()、弹体俯仰角速度()及偏航角速度()。工程上认为，当横滚隔离平台的滚转角()接近0，且滚转角速度()不超过滚转陀螺量程150°s时，滚转隔离有效。

当自旋火箭弹在飞行过程中的姿态发生变化时，各扰动项的信号也会发生变化。由文献[17]可知，实现滚转通道隔离所用支撑轴承的摩擦力矩与转子相对转速之间基本符合正比关系，故当弹体姿态为变加速运动时，滚转、俯仰、偏航角速度及以摩擦力矩为主的电机负载转矩可以视为斜坡扰动信号；当弹体姿态在飞行中发生周期性振荡运动时，滚转、俯仰、偏航角速度及摩擦力矩可以视为正弦扰动信号。

选取与文献[16]相同的特征参数，即控制器参数=30、=150，滚转角速度反馈回路控制参数=5，电机电枢电阻=08 Ω、电感=0000 6 H，电机负载转矩=02 N·m、反电动势系数=494×10V/(°/s)、电磁转矩系数=0264 N·m/A，折合到电机轴上的转动惯量=0027 kg·m，电机定子转速(弹体滚转角速度)=4 4694°/s(15 r/s)。考虑到滚转角≈0而俯仰角ϑ超过70°，俯仰角及偏航角的增益系数=tan ϑsin和=tan ϑcos可视为主要与俯仰角变化相关。

假设各扰动项均以斜坡形式变化，弹体滚转角速度在02 s内从0以斜率22 347变化到4 4694°s，偏航角速度及俯仰角速度在02 s内从0以斜率150变化到30°s，电机负载转矩在02 s内从0以斜率1变化到02 N·m，俯仰角ϑ分别为45°和70°时，横滚隔离平台滚转角速度和滚转角的时间响应情况如图3和图4所示。可以看出，当俯仰角ϑ=45°时，横滚隔离平台仍能正常工作，然而其滚转角速度与阶跃扰动信号作用时相比急剧增大(与文献[16]中结果相比)；当俯仰角ϑ=70°时，平台滚转角速度超过陀螺量程150°s，滚转隔离失效，平台失控。

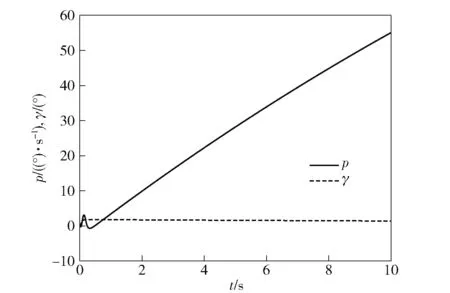
图3 斜坡信号作用下的滚转角速度及滚转角斜坡响应曲线(ϑ=45°)Fig.3 Response curve of roll angular velocity and roll angle under slope disturbances(ϑ=45°)

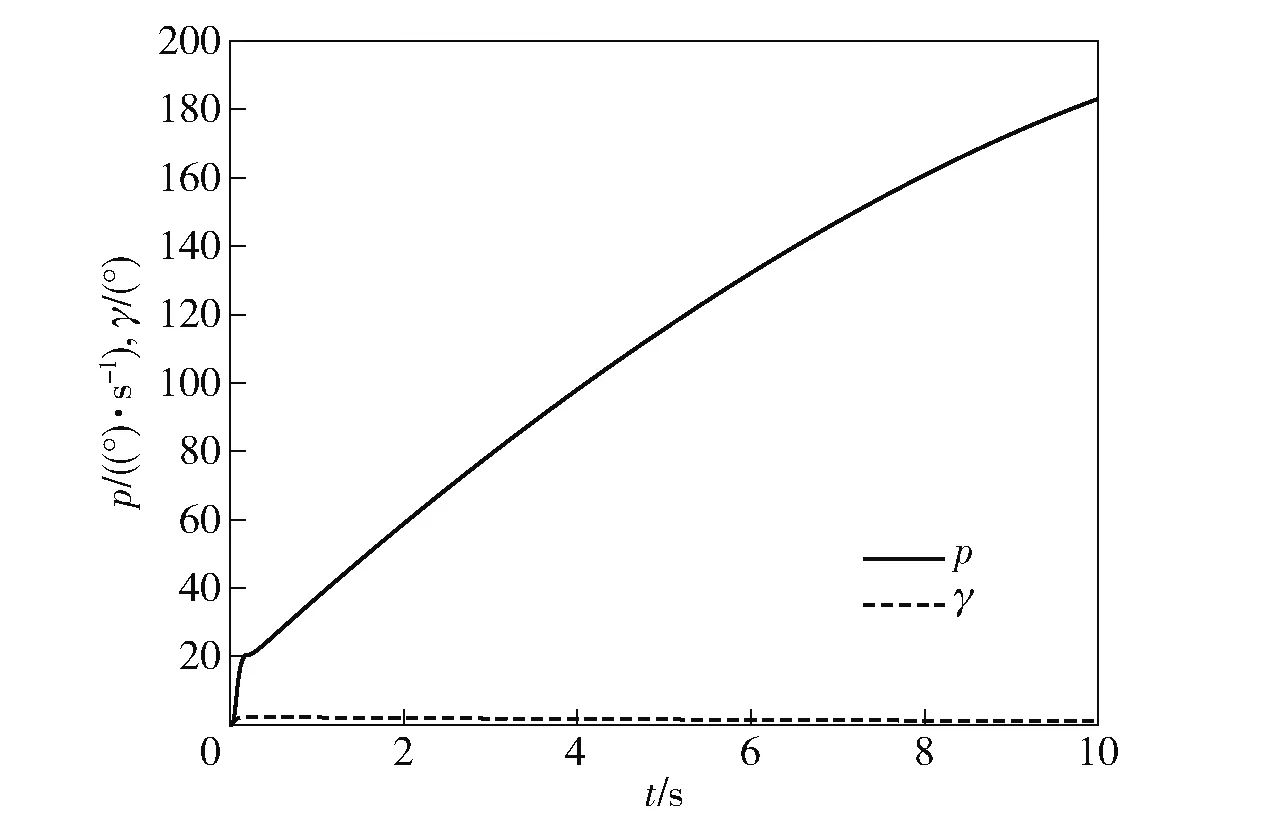
图4 斜坡信号作用下的滚转角速度及滚转角斜坡响应曲线(ϑ=70°)Fig.4 Response curve of roll angular velocity and roll angle under slope disturbances (ϑ=70°)

进一步考虑扰动项均以正弦形式变化，假设弹体滚转角速度幅值为4 4694°s、偏航角速度及俯仰角速度幅值为30°s、电机的负载转矩幅值为02 N·m，四者频率均为12π，俯仰角ϑ分别为45°和70°时，横滚隔离平台滚转角速度和滚转角时间响应曲线如图5和图6所示。可以看出，在俯仰角ϑ=45°时，横滚隔离平台的滚转角速度和滚转角在较小范围内振荡，平台仍能正常工作；在俯仰角ϑ=70°时，平台滚转角在更大的范围内振荡，且平台滚转角速度超过陀螺量程150°s，滚转隔离失效，平台失控。

图5 正弦信号作用下的滚转角速度及滚转角正弦响应曲线(ϑ=45°)Fig.5 Response curve of roll angular velocity and roll angle under sine disturbances(ϑ=45°)

图6 正弦信号作用下的滚转角速度及滚转角正弦响应曲线(ϑ=70°)Fig.6 Response curve of roll angular velocity and roll angle under sine disturbances(ϑ=70°)

总结以上两种仿真结果可知，当电机负载、弹体滚转角速度、偏航角速度和俯仰角速度均为斜坡或者正弦信号时，使用PI控制的横滚隔离系统在大俯仰角飞行情况下滚转隔离失效。

2 系统失效机理分析

2.1 系统模型及稳定性分析

基于图2所示结构图，自旋火箭弹横滚隔离系统的数学模型为

()=[()-()]

(1)

()=()-()

(2)

(3)

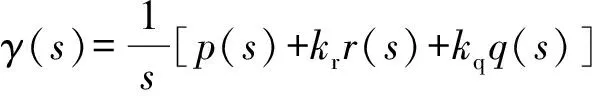
(4)

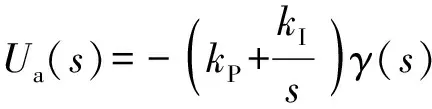
(5)

联立(1)式～(5)式可得输出项()、()的表达式。其中，()可以表示为

()=()()+()()+
()()+()()

(6)

式中：

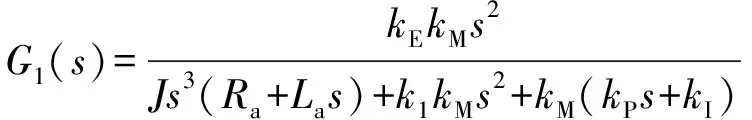
(7)

(8)

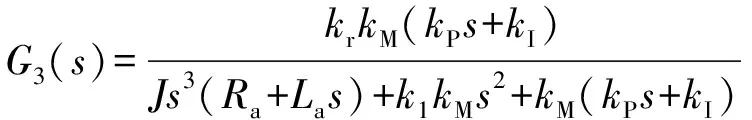
(9)

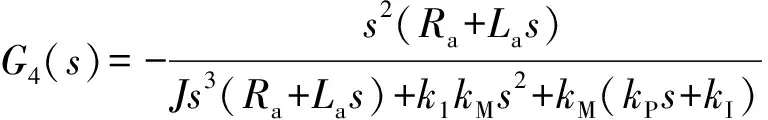
(10)

进而得到以()为输入、()为输出的闭环系统特征方程为：

++++=0

(11)

将各参数代入(11)式，由劳斯判据可判知此闭环系统稳定。

()可以表示为

()=()()+()()+
()()+()()

(12)

式中：

(13)

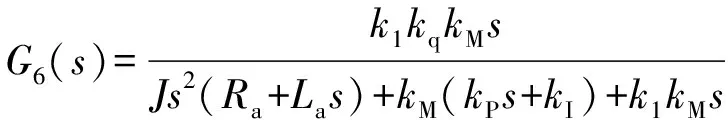
(14)

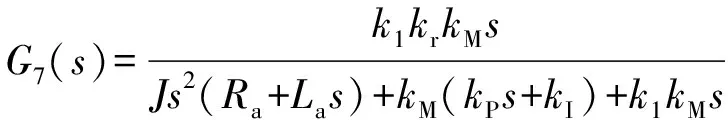
(15)

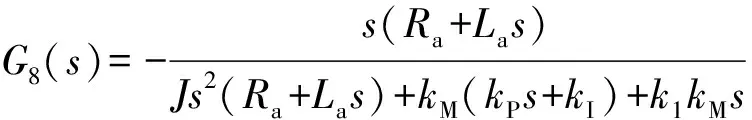
(16)

可得以()为输入、()为输出的闭环系统特征方程为

++(+)+=0

(17)

将各参数代入(17)式中，同样可由劳斯判据判知，此闭环系统稳定。

2.2 阶跃、斜坡及正弦信号稳态输出分析

在系统稳定的基础上，进行系统的稳态误差分析。在计算中，根据扰动信号形式不同，可以分为以下两种情况进行讨论。

221 扰动信号为阶跃和斜坡信号

当扰动信号为阶跃和斜坡信号时，可以直接采用终值定理分析稳态误差，为计算简便，阶跃和斜坡信号均采用单位信号。

1)当()、()、()及()为单位阶跃信号时，系统滚转角速度的稳态输出为

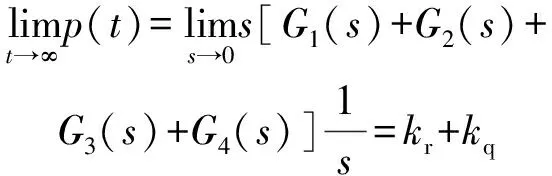
(18)

系统滚转角的稳态输出为

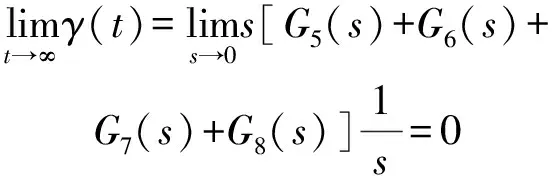
(19)

即滚转角速度的稳态值与偏航及俯仰角速度增益系数有关，而滚转角稳态值为0，这与文献[16]结果一致。

2)当()、()、()及()为单位斜坡信号时，系统滚转角速度的稳态输出为

(20)

系统滚转角的稳态输出为

(21)

可见，当四个扰动均为斜坡信号时，滚转角速度呈持续增大趋势直至无穷大，滚转角的稳态输出为一定值，且可以通过增大积分增益来减小该值，与图3、图4的仿真结果一致。

222()、()、()及()为正弦信号sin()

当()、()、()及()为正弦信号sin()时，终值定理不再适用，横滚隔离平台的滚转角速度和滚转角输出分别为

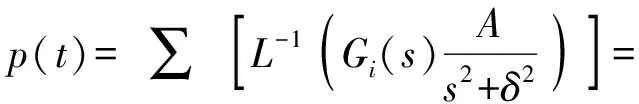
(22)

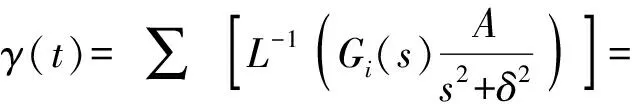
(23)

式中：是拉普拉斯逆变换；=|()|为四个扰动信号分别作用下的传递函数幅频特性，=∠()为上述四个传递函数的相频特性。可以看出，正弦扰动信号作用下的滚转角和滚转角速度为与输入同频率的周期振荡形式，且其幅值与和相关，并随俯仰角增大而急剧增大，导致横滚隔离系统失效，与图5和图6的仿真结果一致。

归纳上述数值仿真和理论分析结果可知，PI控制器作用下的横滚隔离系统可以消除一定形式的外界干扰，如阶跃形式的扰动信号或者小俯仰角飞行情况下的斜坡及正弦扰动信号。但在大俯仰角飞行情况下，若扰动为斜坡或正弦信号时，PI控制器作用下的横滚隔离平台滚转角速度超出滚转陀螺量程，横滚隔离系统失效，因此有必要设计适应信号形式范围更广的控制器。

3 横滚隔离系统的自抗扰控制器

3.1 自抗扰横滚隔离系统

韩京清等提出的自抗扰控制技术是一种性能更优、应用也比较广泛的控制方法。自抗扰控制器(ADRC)由微分跟踪器(TD)、非线性状态误差反馈控制律(NLSEF)和扩张状态观测器(ESO)组成。其核心思想是将系统模型的未知动态和外界干扰均看作系统输入，并进行自动估计和补偿，因此具有更强的适应性和鲁棒性。

自抗扰控制方法对系统精度要求不高，在各种干扰情况下也能够保持较好的控制效果，已广泛应用于电机控制等领域。近年来，随着机载计算机技术的发展，自抗扰控制方法在航空航天控制领域也得到了一些应用，并表现出较好的控制品质。为了解决当扰动为斜坡或正弦信号时，自旋火箭弹横滚隔离系统在大俯仰角飞行情况下的失效问题，本文提出使用自抗扰控制方法对横滚隔离系统原有的PI控制器进行优化设计。

在图2所示使用PI控制器的横滚隔离系统基础上，将PI控制器换为自抗扰控制器，得到采用自抗扰控制器的横滚隔离系统结构如图7所示。以滚转角速度为输出的横滚隔离系统，如(11)式所示为四阶系统，故需要采用四阶微分跟踪器、五阶扩张状态观测器对自抗扰控制器进行设计。

图7 自抗扰横滚隔离系统结构图Fig.7 Schematic diagram of the roll-isolated system with ADRC

3.2 四阶微分跟踪器设计

对于如下阶系统：

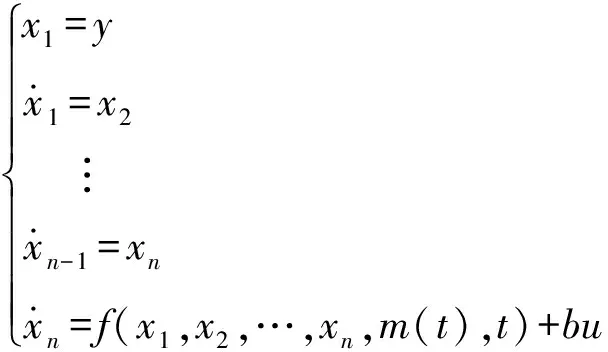
(24)

式中：为输出变量；为控制变量；为放大系数；()为外部干扰；(,,…,,(),)为总干扰(内部干扰与外部干扰之和)。由微分近似公式推导高阶微分跟踪器的方法，该阶系统近似微分传递关系为

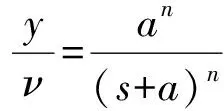
(25)

根据(25)式设计四阶微分跟踪器为

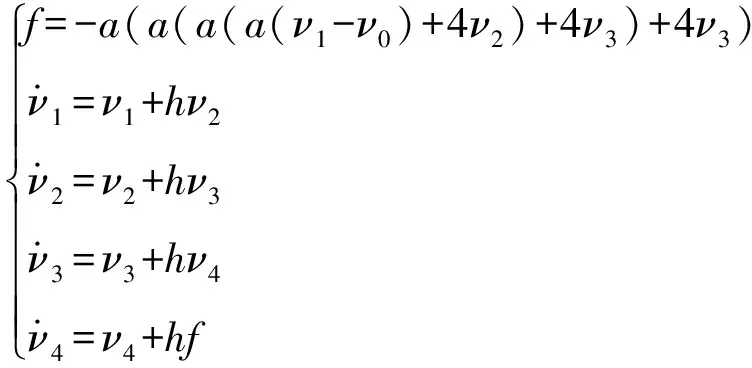
(26)

式中：为输入信号；、为高阶微分跟踪器参数，当取较大值,取较小值时，微分跟踪器具有较好性能。

3.3 五阶扩张状态观测器设计

将二阶系统三阶扩张状态观测器的设计方法推广至四阶系统，得到如下的扩张状态观测器：

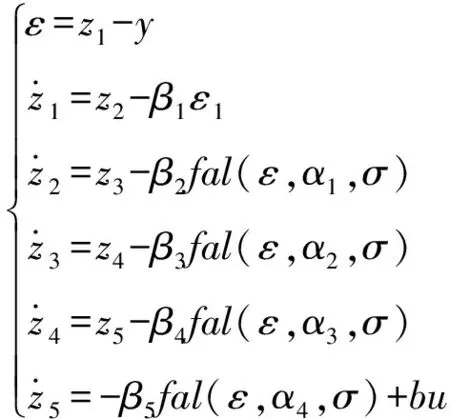
(27)

非线性反馈控制律为

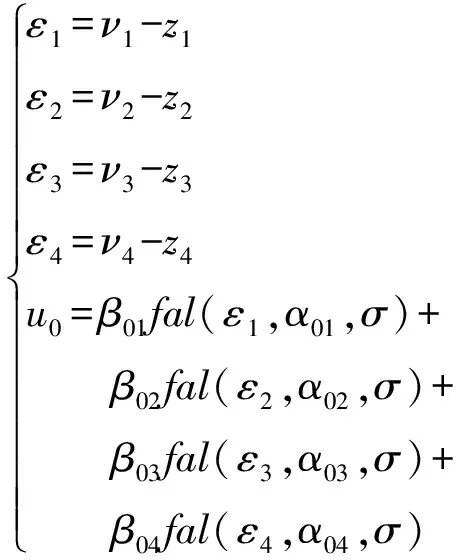
(28)

式中：为状态误差；、、、、为扰动估计值；、、、、、、、、、为扩张状态观测器ESO的增益参数；、、、、、、、为非线性状态误差反馈控制律NLSEF的参数。控制量由误差反馈控制量和扰动估计值求得：

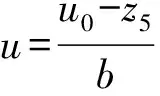
(29)

(26)式～(29)式即构成了横滚隔离系统的自抗扰控制器。

为验证四阶系统自抗扰控制器的有效性，取微分跟踪器TD的参数、分别为650、0000 5，扩张状态观测器ESO的增益参数、、、、分别为20 000、10 000、500 000、10 000、30 000，、、、分别为12、12、12、12，为05，非线性状态误差反馈控制律NLSEF的参数、、、分别为20、10、1 000、50，、、、分别为06、12、09、15。分别在输入信号为斜坡和正弦形式下，对系统进行仿真，得到输入信号与扰动估计值。图8给出了输入在2 s内以斜率15从0变化到30的斜坡信号与扩张状态观测器对扰动的估计值对比图。图9给出了输入为幅值30、频率12π的正弦信号与扩张状态观测器对扰动的估计值对比图。由图8、图9可知，在输入信号是斜坡及正弦形式时，此四阶系统的扩张状态观测器可以对扰动进行估计，自抗扰控制器有效。

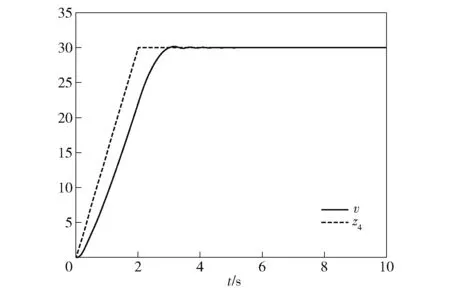
图8 斜坡输入信号与扰动估计值对比图Fig.8 Comparison of slope signal and disturbance estimation

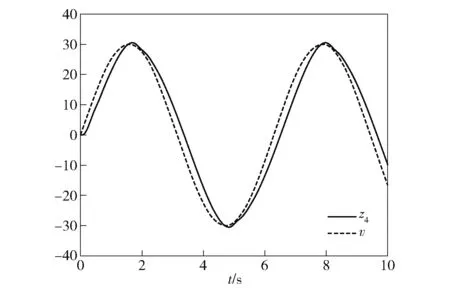
图9 正弦输入信号与扰动估计值对比图Fig.9 Comparison of sine signal and disturbance estimation

4 自抗扰横滚隔离系统的控制性能

为验证使用自抗扰控制器的横滚隔离系统在大俯仰角飞行情况下的工作有效性，使用与12节中相同的系统参数对横滚隔离平台的滚转角速度及滚转角进行仿真。

4.1 斜坡扰动下的自抗扰横滚隔离系统仿真

图10和图11分别给出了俯仰角ϑ=45°及ϑ=70°时，斜坡信号作用下横滚隔离平台滚转角速度和滚转角的时间响应曲线。可以看出，当弹体滚转角速度以斜坡形式快速变化时(斜率为22 347)，横滚隔离平台的滚转角速度仅保持1°s以内的低速变化，并有效避免了振荡，平台滚转角维持在0附近，滚转隔离有效，横滚隔离系统正常工作。

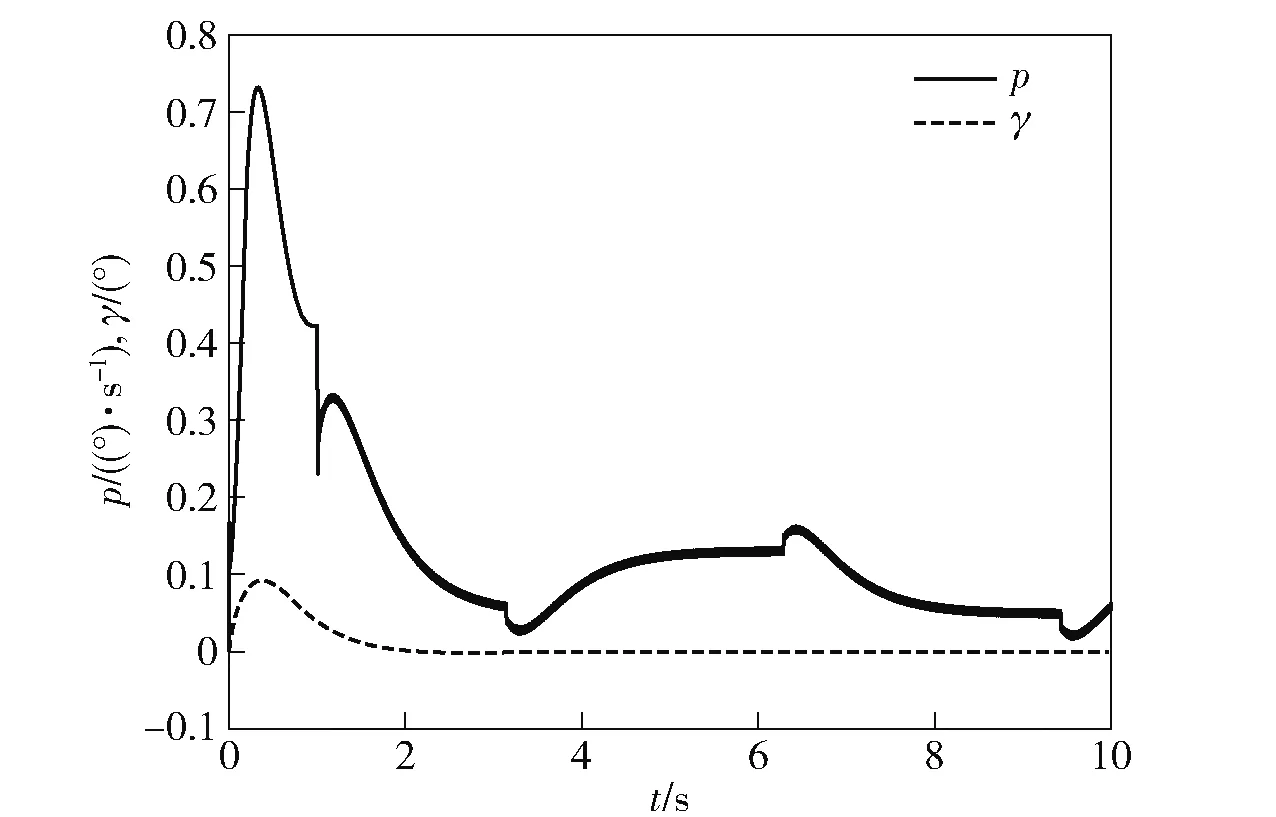
图10 采用自抗扰控制器时的滚转角速度及滚转角斜坡响应曲线(ϑ=45°)Fig.10 Response curve of roll angular velocity and roll angle under slope disturbances with ADRC(ϑ=45°)

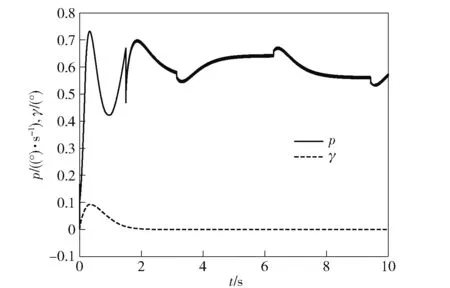
图11 采用自抗扰控制器时的滚转角速度及滚转角斜坡响应曲线(ϑ=70°)Fig.11 Response curve of roll angular velocity and roll angle under slope disturbances with ADRC(ϑ=70°)

4.2 正弦扰动下的自抗扰横滚隔离系统仿真

图12和图13分别给出了俯仰角ϑ=45°及ϑ=70°时，正弦扰动信号作用下横滚隔离平台滚转角速度和滚转角的时间响应曲线。可以看出，当弹体滚转角速度以正弦周期变化时，平台滚转角速度在1°s的较小范围内周期变化，平台滚转角同样维持在0附近，横滚隔离有效。

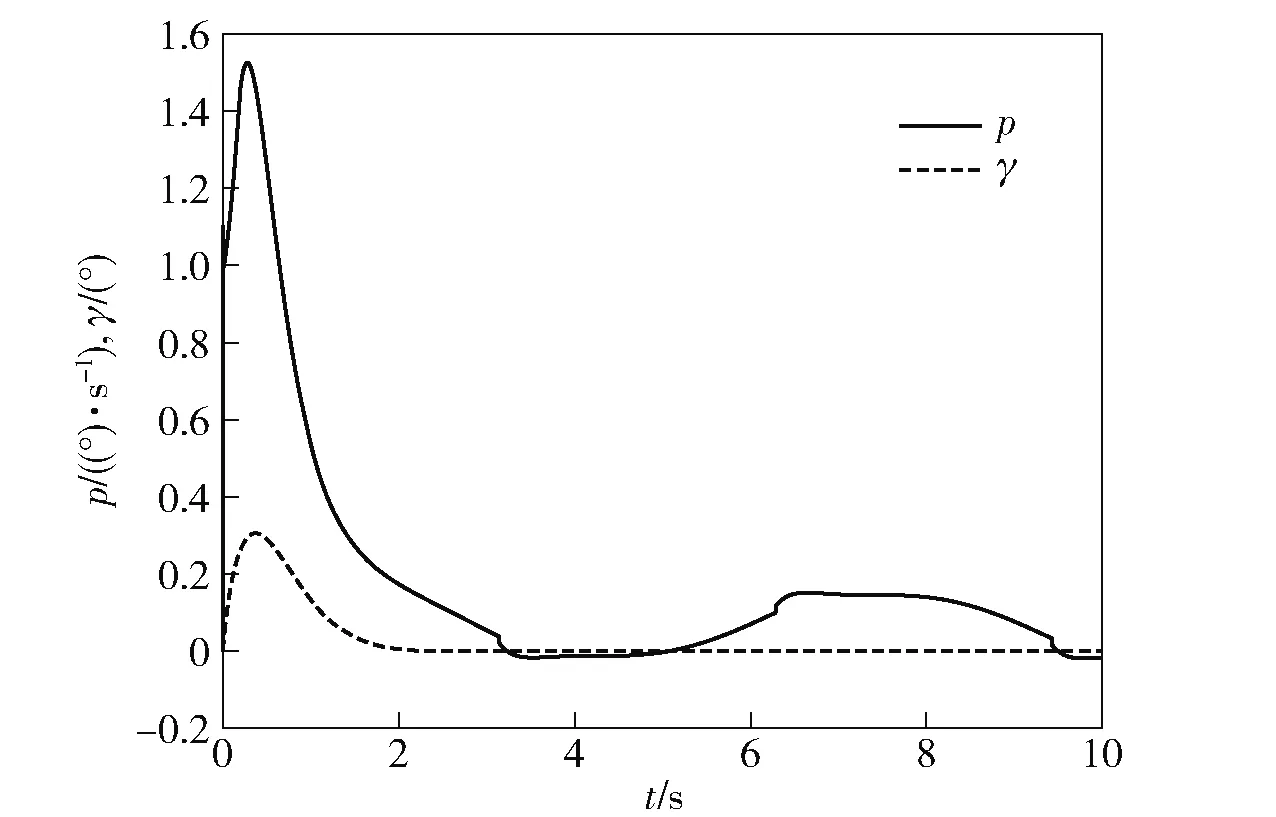
图12 采用自抗扰控制器时的滚转角速度及滚转角正弦响应曲线(ϑ=45°)Fig.12 Response curve of roll angular velocity and roll angle under sine disturbances with ADRC(ϑ=45°)

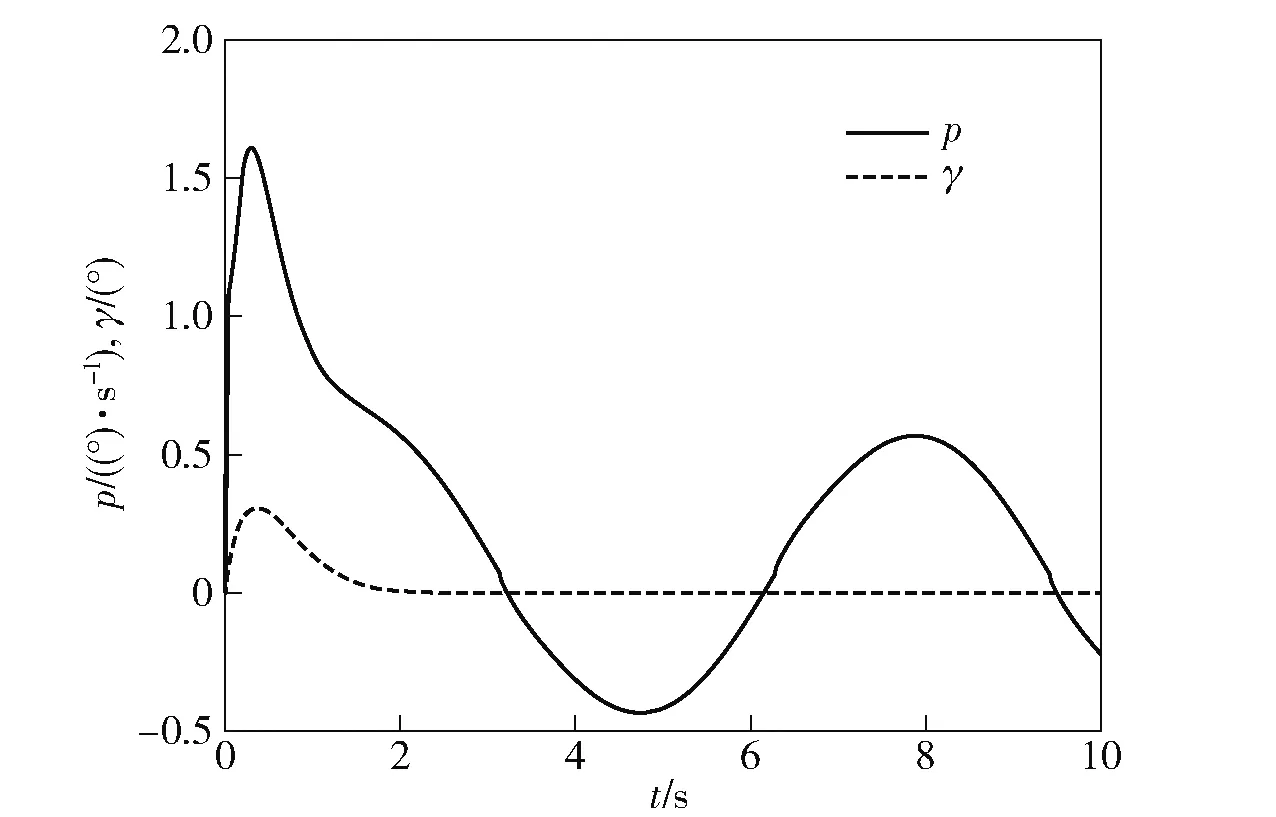
图13 采用自抗扰控制器时的滚转角速度及滚转角正弦响应曲线(ϑ=70°)Fig.13 Response curve of roll angular velocity and roll angle under sine disturbances with ADRC(ϑ=70°)

综合以上两组仿真结果可以发现，采用自抗扰控制器的横滚隔离系统，可以在自旋火箭弹大俯仰角飞行情况下，有效应对斜坡和正弦形式的干扰，并均可以将横滚隔离平台的滚转角速度控制在1°/s以内的较小范围内，将滚转角控制在0附近，从而保证滚转隔离有效，横滚隔离系统正常工作。

5 结论

1)当自旋火箭弹在大俯仰角飞行情况下，且扰动为斜坡或正弦信号时，采用PI控制器的横滚隔离系统会发生滚转陀螺超量程进而导致滚转隔离失效的现象。

2)在建立采用PI控制器的横滚隔离系统数学模型基础上，分别通过理论分析和数值仿真，揭示了斜坡和正弦扰动作用下滚转隔离失效的机理。

3)设计了自旋火箭弹横滚隔离系统的自抗扰控制器。数值仿真结果显示，所设计的自抗扰控制器可以应对大俯仰角飞行情况下的斜坡和正弦扰动，可将横滚隔离平台的滚转角速度控制在1°/s以内的较小范围内，并将滚转角控制在0附近，保证了滚转隔离的有效性。

[1] 杨树兴. 陆军多管火箭武器的发展与思考[J]. 兵工学报, 2016, 37(7): 1299-1305.

YANG S X. Progress and key points for guidance of multiple launch rocket systems[J]. Acta Armamentarii, 2016, 37(7): 1299-1305. (in Chinese)

[2] 陈成, 赵良玉, 谢浩怡, 等. 单通道控制旋转弹角运动的复分析方法[J]. 兵工学报, 2021, 42(2): 308-319.

CHEN C, ZHAO L Y, XIE H Y, et al. Complex analysis for angular motion of a spinning projectile with one pair of canards[J]. Acta Armamentarii, 2021, 42(2):308-319. (in Chinese)

[3] 雷娟棉, 张嘉炜, 谭朝明. 小攻角下船尾外形对旋转弹丸马格努斯效应影响的数值研究[J]. 兵工学报, 2017, 38(9): 1705-1714.

LEI J M, ZHANG J W, TAN Z M. Influence of boattail on the Magnus effect of spinning non-finned projectile at small angles of attack[J]. Acta Armamentarii, 2017, 38(9): 1705-1714. (in Chinese)

[4] 王波兰, 李克勇, 杨永强. 近程/末端旋转导弹发展及关键技术综述[J]. 上海航天, 2017, 34:1-6.

WANG B L, LI K Y, YANG Y Q. Review of development and key techniques of rolling airframe missiles[J]. Aerospace Shanghai, 2017, 34: 1-6. (in Chinese)

[5] 张平, 赵志明, 贾波, 等. 尾翼稳定火箭弹高原姿态运动规律研究[J]. 兵工学报, 2016, 37(8): 1345-1350.

ZHANG P, ZHAO Z M, JIA B, et al. Research on attitude motion law of rockets on plateau[J]. Acta Armamentarii, 2016, 37(8): 1345-1350. (in Chinese)

[6] 丁天宝, 何朝, 王良明, 等. 高速旋转炮弹宽海拔弹道解算方法[J]. 兵工学报, 2021, 42(1):209-213.

DING T B, HE Z, WANG L M, et al. Calculation method of firing trajectory of high spinning projectile adapted to wide altitude[J]. Acta Armamentarii, 2021, 42(1): 209-213. (in Chinese)

[7] 杨树兴, 赵良玉, 闫晓勇. 旋转弹动态稳定性理论[M]. 北京: 国防工业出版社, 2014.

YANG S X, ZHAO L Y, YAN X Y. Dynamic stability of spinning missiles[M]. Beijing: National Defense Industry Press, 2014. (in Chinese)

[8] IMBAULT J, TJULIN H, KINNEY R, et al. Mini-RIMS-a miniature roll-stabilized inertial measurement system[C]∥Proceedings of the 7th Conference on Sounding Rockets, Ballons and Related Space Systems. Ocean City, MD, US: AIAA, 1986:35-43.

[9] YANG Z L, MO B, NIE Z. Design on MEMS Based Roll-Isolated SINS in Spinning Projectile[J]. Telecom Market, 2013(5): 46-51.

[10] 李杰, 赵诣, 刘俊, 等. 高旋弹药飞行姿态测量用半捷联MEMS惯性测量装置研究[J]. 兵工学报, 2013, 34(11): 1398-1403.

LI J, ZHAO Y, LIU J, et al. Research on semi-strapdown MEMS inertial measurement device for flight attitude measurement of high-speed rotating ammunition[J]. Acta Armamentarii, 2013, 34(11): 1398-1403. (in Chinese)

[11] 李杰, 刘俊. 旋转弹用半捷联惯性测量系统数据传输技术[J]. 弹箭与制导学报, 2014, 34(4): 57-60.

LI J, LIU J. Research on data transmission technology for rotating ammunition with semi-strapdown inertial measurement system[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2014, 34(4): 57-60. (in Chinese)

[12] 周琪, 秦永元, 赵长山. 旋转弹用横滚隔离捷联惯导稳定回路设计[J]. 中国惯性技术学报, 2009, 17(4): 383-387.

ZHOU Q, QIN Y Y, ZHAO C S. Design on stabilization loop of roll-isolated SINS in spinning projectile[J]. Journal of Chinese Inertial Technology, 2009, 17(4): 383-387. (in Chinese)

[13] 周琪, 秦永元, 杨鹏翔. 横滚隔离激光捷联惯导系统稳定回路自抗扰控制[J]. 测控技术, 2009, 28(11): 95-100.

ZHOU Q, QIN Y Y, YANG P X. Active disturbance rejection control of the stabilizing loop for roll-isolated laser gyro strapdown inertial navigation system[J]. Measurement & Control Technology, 2009, 28(11): 95-100. (in Chinese)

[14] SHI Y S, WANG B, DONG M J, et al. Research of Roll-Isolated Gimbal Platform and a Two-Position Initial Alignment Scheme of SINS in Spinning Projectile[J]. Advanced Materials Research, 2012, 383-390: 4115-4120.

[15] 刘一鸣, 李杰, 王一焕, 等. 旋转弹用轴向减旋平台控制系统设计[J]. 电子器件, 2017, 40(4): 965-972.

LIU Y M, LI J, WANG Y H, et al. Design of the control system for axial anti-rotation platform used in rotating ammunition[J]. Chinese Journal of Electron Devices, 2017, 40(4): 965-972. (in Chinese)

[16] SONG J C, YANG S X, XIONG F F. Control failure of the roll-isolated inertial navigation system under large pitch angle[J]. Chinese Journal of Aeronautics, 2020, 33(10): 2707-2715.

[17] 朱爱华, 朱成九, 张卫华. 滚动轴承摩擦力矩的计算分析[J]. 轴承, 2008(7): 1-3.

ZHU A H, ZHU C J, ZHANG W H. Analysis on calculation of friction torque of rolling bearings[J]. Bearing, 2008(7): 1-3. (in Chinese)

[18] 韩京清, 王伟. 非线性跟踪- 微分器[J]. 系统科学与数学, 1994, 14(3): 177-183.

HAN J Q, WANG W. Nonlinear tracking-differentiator[J]. Journal of Systems Science and Mathematical Sciences, 1994, 14(3): 177-183. (in Chinese)

[19] 韩京清. 自抗扰技术：估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008.

HAN J Q. Active disturbance rejection control technique-the technique for estimating and compensating the uncertainties[M]. Beijing: National Defense Industry Press, 2008. (in Chinese)

[20] 赵春哲, 黄以. 基于自抗扰控制的制导与运动控制一体化设计[J]. 系统科学与数学, 2010, 30(6): 742-751.

ZHAO C Z, HUANG Y. ADRC based integrated guidance and control scheme[J]. Journal of Systems Science and Mathematical Sciences, 2010, 30(6): 742-751. (in Chinese)

[21] 唐彬彬, 徐道明, 吴若鸷. 永磁同步电机自抗扰控制调速系统[J]. 电机与控制应用, 2020, 47(3):12-16.

TANG B B, XU D M, WU R Z. Active disturbance rejection control speed regulation system for PMSM[J]. Electric Machines & Control Application, 2020, 47(3): 12-16. (in Chinese)

[22] 岳彬, 马文, 呼卫军. 高超声速飞行器的自适应容错控制[J]. 兵工学报, 2021, 42(3): 521-529.

YUE B, MA W, HU W J. Adaptive fault-tolerant control of hypersonic vehicles[J]. Acta Armamentarii, 2021, 42(3): 521-529. (in Chinese)

[23] 韦常柱, 琚啸哲, 徐大富, 等. 垂直起降重复使用运载器返回制导与控制[J]. 航空学报, 2019, 40(7): 322782.

WEI C Z, JU X Z, XU D F, et al. Guidance and control for return process of vertical takeoff vertical landing reusable launching vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(7): 322782. (in Chinese)

[24] 张茜丹, 尹达一. 自抗扰控制器在高阶系统中仿真实现[J]. 航天控制, 2018, 36(1): 3-13.

ZHANG X D, YIN D Y. Simulation study of active disturbance rejection controller for high order systems[J]. Aerospace Control, 2018, 36(10): 3-13. (in Chinese)