一类四阶常微分方程两点边值问题的奇摄动

胡永生

(福建农业职业技术学院 通识教育学院, 福建 福州 350007)

0 引言

奇摄动问题广泛出现于物理学、医学、生物学、力学和天文学等相关的数学模型中.从实际问题中抽象出来的数学模型,常常是非线性,变系数的微分方程,一般又附以非线性的边界条件或初始条件.这导致绝大多数情况下无法获得精确解.求近似解的一种最有效的方法是摄动法,也称渐近方法[1],如变形坐标法,平均法,匹配渐近展开法,合成展开法,WKB法以及微分不等式理论等[1-5].在工程应用中,弹性梁模型可以表达为一个四阶常微分方程.弹性梁是现代飞机、轮船、桥梁、建筑等最基本也是最重要的结构,所以四阶常微分方程的各种边值问题,引起了众多学者的关注和研究[6-11].由于四阶微分方程的各类问题往往都具有现实背景,除了方程本身是一个重要的因素外,方程所附加的边值条件或初值条件,往往也起着重要作用,不同类型的初(边)值条件,对应着不同的现实模型.如两点简单支撑的弹性梁、一端简单支撑,一端自由活动的弹性梁就对应着不同的边界条件[12-13].通常情况下,对于四阶常微分方程初(边)值问题的研究,人们更多采用通过变换将四阶边值问题转化为二阶微分方程组,进而利用锥拉伸锥压缩不动点定理、拓扑度理论以及上下解方法等方式进行研究.但是,借助于伸展变换的引入,利用匹配渐近展开法和Van Dyke匹配原则[1,3-4],很多高阶微分方程的初(边)值问题也能求得渐近解.现研究一类四阶常微分方程的边值问题,先由匹配渐近展开法分别构造外部解和内层解,再通过Van Dyke匹配原则将内外解匹配“缝接”,得到边值问题一致有效的复合解.

1 预备知识

1.1 内(外)解与匹配渐近展开法[1]

1.2 Van Dyke匹配原理[1,3]

1964年,斯坦福大学航空航天系Milton 在处理翼型布局理论的一些奇异摄动问题过程中,需要解决以下系统的“内层解”与“外层解”的匹配问题[5].

提出了一种匹配原则(Van Dyke匹配原理),即

2 渐近解的构造

考虑如下一类四阶常微分方程两点边值奇摄动问题

(1)

其中0<ε≪1是小参数.注意到边值问题(1)的方程中左边两项的导数阶数差为2,由文[3]可知，该边值问题将在左右端点各存在一个边界层.

2.1 外部解的构造

由文[3]可知,假设边值问题(1)的外部解的二阶渐近展开式为

yo(x,ε)=y0(x)+εy1(x)+ε2y2(x)+…

(2)

将式(2)代入边值问题(1)的第一个方程,并平衡方程两边关于ε的同次幂可得

(3)

式(3)的解分别为

(4)

由于外部解不满足任何边界条件,故Ai,Bi,(i=0,1,2)为待定积分常数,需要在之后的匹配中确定.因此,边值问题(1)的外部解的二阶近似为

(5)

2.2 x=0处边界层解的构造

(6)

当λ=1时,其特异极限为

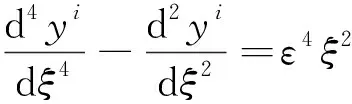
(7)

由于yi应在点x=0处一致有效,而当x=0时ξ=0,故方程(7)应满足的初值条件为

(8)

为求得点x=0处边界层解的渐近展开式,假设yi具有如下形式

yi=Y0(ξ)+εY1(ξ)+ε2Y2(ξ)+…

(9)

将式(9)代入到式(7)和式(8)，并平衡关于ε的幂，可得

(10)

(11)

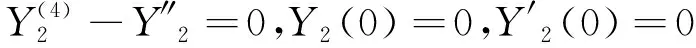
(12)

方程(10)～(12)的通解分别为

Yi=ci0+ci1ξ+ci2eξ+ci3e-ξ,(i=0,1,2)

(13)

对于Y0,显然应有系数c02=0,否则Y0→+∞,(ε→0),将导致无法与外部解匹配.再将方程(10)中初始条件代入可得c00=-c01,c03=c01,故

Y0(ξ)=-c01+c01ξ+c01e-ξ

(14)

同理可得

Y1(ξ)=1-c11+c11ξ+(c11-1)e-ξ

(15)

Y2(ξ)=-c21+c21ξ+c21e-ξ

(16)

至此,可得边值问题(1)在点x=0处边界层函数的二阶近似为

yi=-c01+c01ξ+c01e-ξ+ε(1-c11+c11ξ+(c11-1)e-ξ)+

ε2(-c21+c21ξ+c21e-ξ)+O(ε3)

(17)

其中,常数ci1,(i=0,1,2)需要在与外解的匹配中确定.

2.3 x=0处三项边界层解与三项外解的匹配

三项外解

利用伸展变量表示

展开为ε的幂级数

yo=B0+ε(A0ξ+B1)+ε2(A1ξ+B2)+…

三项外解的内展开

三项内解

yi～-c01+c01ξ+c01e-ξ+ε(1-c11+c11ξ+(c11-1)e-ξ)+ε2(-c21+c21ξ+c21e-ξ).

利用外解变量表示

展开为ε的幂级数(为避免展开式中出现ε的负数幂导致无法匹配,令c01=0),

yi=c11x+ε(1-c11+c21x)+ε2(-c21)+…

三项内解的外展开

A0=c11,B0=0,A1=c21,B1=1-c11,B2=-c21.

至此,可将边值问题(1)的外解改写为

(18)

2.4 x=1处边界层解的构造

(19)

令ε→0,易知,当v=1时，式(19)的特异极限为

(20)

由于yI应在x=1处一致有效,而当x=1时ζ=0,故式(20)应满足的初值条件为

yI′(0)=-2ε,yI″(0)=3ε2

(21)

现假设边值问题(1)在点x=1附近的边界层函数具有如下形式

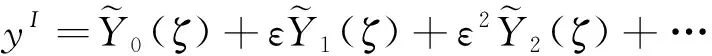
(22)

将式(22)代入到式(20)和式(21)并平衡两端关于ε的同次幂,可得

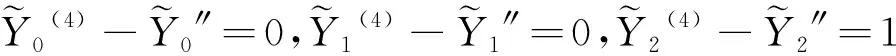
(23)

分别满足的初始条件为

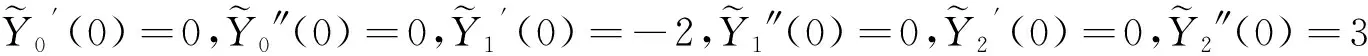
(24)

联立式(23)和式(24),并剔除指数增长项，可得

至此,可得边值问题(1)在点x=1处的边界层函数的二阶近似为

(25)

其中常数ki0,(i=0,1,2)需要在与外解的匹配中确定.

2.5 x=1处三项边界层解与三项外解的匹配

三项外解

利用伸展变量表示

展开为ε的幂级数

三项外解的内展开

三项内解

利用外解变量表示

展开为ε的幂级数

三项内解的外展开

至此,式(25)可改写为

(26)

由式(5)、式(17)和式(26),以及文[3]可知,边值问题(1)具有以下一致有效的二阶渐近解

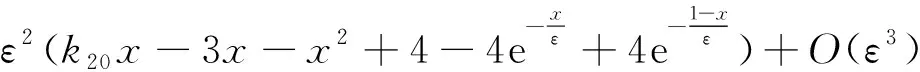
(27)

注二阶近似下k20∈R.

3 四阶常微分方程边值问题渐近解的数值验证

为验证以上渐近展开法所得渐近解的正确性,现取定ε=0.001,k20=1,将边值问题(1)的二阶渐近解式(27)与数值解对照,结果见表1.

表1 渐近解与数值解的对照

由表1可见,根据匹配渐近展开法得到的渐近解式(27),相对于数值解达到了较高的精度,这验证了渐近解的正确性.

4 结语

相比于各文献中采用的锥拉伸锥压缩不动点定理、拓扑度理论、上下解方法、全连续算子的Schauder不动点定理等方法,对四阶常微分方程边值问题的研究,匹配渐近展开法和Van Dyke匹配原则能简便快速地获得边值问题的任意阶渐近解,并且具有足够高的精度.同时,对于完全四阶常微分方程以及其他类型的边界条件,依托于实际应用,仍具有进一步研究的意义.