基于峭度的可变步长随机信息梯度算法

景绍学， 孙 伟, 张 翔

(淮阴师范学院 物理与电子电气工程学院, 江苏 淮安 223300)

0 引言

参数估计是利用动态系统的观测数据建立数学模型的过程,该数学模型可以反映系统的某些动态特性[1]．目前,在系统辨识和参数估计方面已有大量的研究成果[2-4]．参数估计过程中的一个重要问题是选择模型结构[5]．动态模型有很多种,如:线性模型、非线性模型、确定性模型、随机模型等,其中FIR模型是较简单的模型[6-8]．研究结果表明,只要阶数足够高,FIR模型能够以任意精度逼近任何稳定的线性系统．近几十年来,FIR模型在系统辨识、参数估计和信号处理中得到了广泛的应用[9-11]．如：为了辨识时变FIR模型,基于系统参数的预估计,提出了一种解耦卡尔曼滤波算法[9];针对具有二值观测数据的FIR模型辨识问题,推导了一种基于极大似然的辨识算法,并对其性能进行了讨论[10];为了估计线性时变马尔可夫模型,提出了一种无偏FIR滤波器[11]．尽管对某些FIR模型的辨识效果良好,但现有的算法大多只涉及白噪声或正态分布噪声的FIR模型．

脉冲噪声通常可见于许多工业信号中,如图像信号、音频信号和通信信号等[12-13]．基于现有辨识准则的算法，如：最小二乘(LS)准则、均方误差(MSE)准则和最大似然(ML)准则，可能会产生不能令人满意的辨识结果[14-15]．主要原因有:LS和MSE准则仅捕获数据中的二阶统计量,而ML准则需要数据分布的先验信息,而许多情况下是未知的．为了考虑高阶统计量,人们研究了许多非均方误差准则,其中信息准则受到广泛关注[16-17]．与均方误差准则相比,信息准则采用了某种熵,如Shannon熵、Renyi熵和交叉熵来推导辨识算法[18-19]．基于信息准则的算法在非高斯环境下表现出优异的性能[20-21]．

因此,为了辨识带有脉冲噪声的FIR模型,推导了一种基于信息准则的算法,其名称为随机信息梯度算法．本文的主要工作如下:

1) 为了获得脉冲噪声下FIR模型的精确估计,提出了一种基于最小误差熵的随机信息梯度算法;

2) 由于梯度算法收敛速度慢,算法中引入了基于峭度的可变步长;

3) 为了实现该算法,通过理论分析和实验仿真,给出了一种确定最大步长的实用方法．

本文描述了所要估计的FIR模型，提出了一种基于峭度的变步长随机信息梯度算法，通过几个数值算例验证了所提出的算法，最后给出了主要结论．

1 问题描述

考虑图1所示的FIR模型,其中u(k)和y(k)分别是系统的输入和输出．B(z-1)是由阶数为nb的FIR函数描述的线性动态模型．FIR模型受到脉冲噪声v(k)的污染．

图1 FIR模型框图

从图1可以看出,输出y(k)可以写成

y(k)=B(z-1)u(k)+v(k)=

b1u(k-1)+b2u(k-2)+…+bnbu(k-nb)+v(k)=φT(k)θ+v(k)

(1)

其中

(2)

2 辨识算法

对于式(1)所示的参数化模型,定义瞬时误差为

e(k)=y(k)-φT(k)θ

(3)

若误差的概率密度函数为f(e),则误差的Shannon熵可以表示为[22]

H(e)=E[-logf(e)]

(4)

其中未知的f(e)可通过Parzen窗口方法估计得到[19],即

(5)

式中κσ(·)表示核宽度为σ的核函数．

定义Δeki=e(k)-e(i),f(e)的一个窗长L的估计可通过下式得到[23]

(6)

因此,误差熵H(e)在k时刻的一个估计为

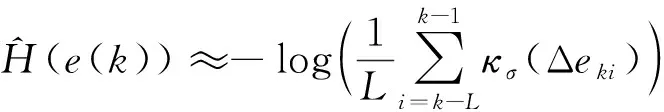
(7)

采用高斯核函数,上述误差熵对于参数的梯度为

(8)

于是得到估计参数向量θ的随机信息梯度(SIG)算法为

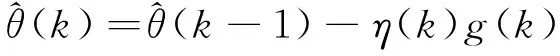
(9)

其中η(k)表示步长,本文将利用峭度获得一个可变步长．

众所周知,SIG算法收敛较慢．为了加速算法收敛,采用了如下的变步长策略[24]:

η(k)=ηm(1-e-α|K(e(k))|)

(10)

其中η(k)表示最大步长(接下来给出经验公式);α为[1,10]的一个松弛因子,由用户确定;K(·)表示一个受误差影响的可变峭度．

(11)

式中,ξ可在(0,1)之间选择,其典型值在[0.1,0.4]之间．为了获得灵活的峭度,引入可变因子ρ(k),得到

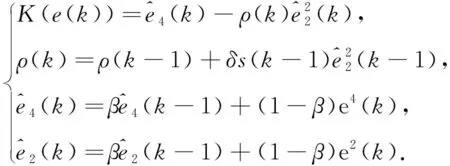
(12)

其中s(k-1)表示K(e(k-1))的符号,常数δ,β可分别在(0,0.1)和(0,1)范围内取值．

3 实验

考虑如下的FIR模型

y(k)=0.5u(k-1)+1.1u(k-2)+0.8u(k-3)+

0.6u(k-4)+0.2u(k-5)+0.1u(k-6)+v(k)

(13)

实验时,u(k)采用一个伪随机序列,v(k)为一个脉冲噪声．数据长度为600．用c表示脉冲添加的百分比．例如,c=5%时,随机添加N×c=600×5%=18个脉冲噪声到数据序列中．本文中,Parzen窗长度取值为3,高斯核函数的核宽度取值为1．所用数据的曲线如图2所示．

1) 不同ηm时

为验证ηm对所提算法性能的影响,令ηm=0.01,0.05,0.10时利用所提出的VSS-SIG算法对上述FIR模型进行辨识．不同ηm时的估计误差曲线如图3所示．

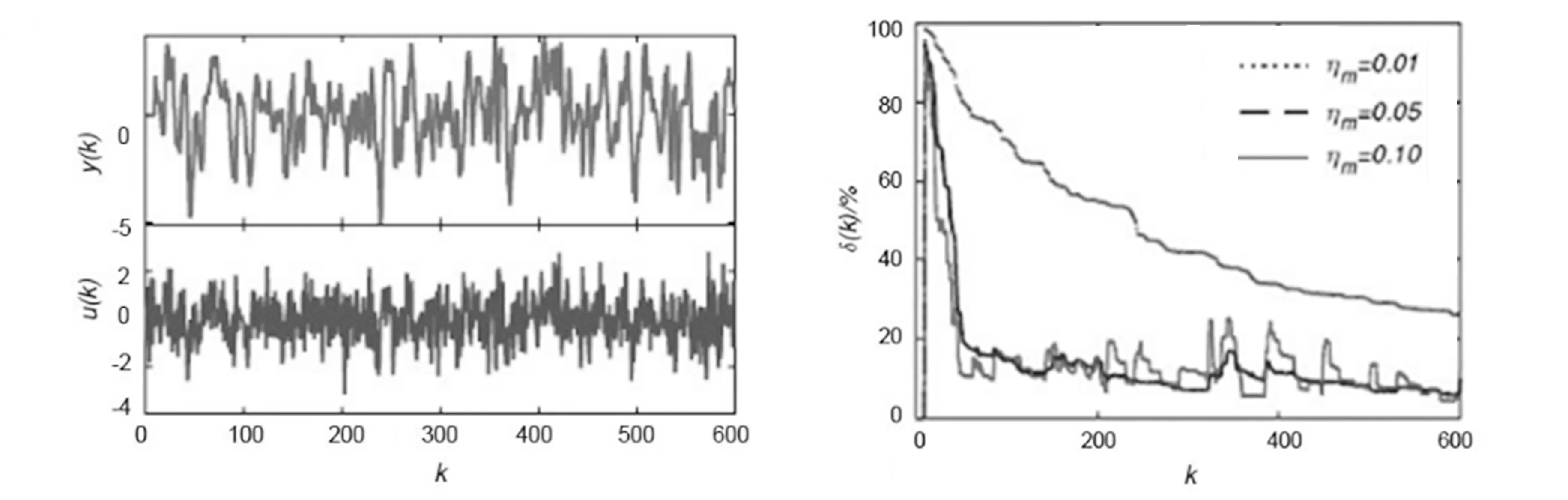
图2 数据曲线 图3 不同ηm时的误差曲线

分析可见: ①总体上看,对于给定的一个ηm,参数估计误差随辨识的进行而减小; ②ηm取较小数值时(如0.01),估计误差变化缓慢,但是估计误差波动较小;相反,ηm取较大数值时,算法收敛很快,但误差波动较大; ③对于较小数据集的辨识,较大的ηm可以迅速地得到交精确的估计值,但是过大的ηm会带来参数估计值的大幅波动．

2) 不同α时

测试了α对所提算法性能的影响．不同α时的误差曲线如图4所示．分析可见： ①对于给定α,估计误差随k的增加而减小; ②误差曲线的开始,3条曲线差别不大;随后,曲线开始分化:较小的α对应的曲线在上面,较大的α对应的误差曲线在底部．结果表明,较小的α会导致步长的快速衰减,从而带来相对较慢的收敛速度,但是差别不大;反之亦然．

图4 不同α时的误差曲线 图5 不同n时的误差曲线

3) 不同n时

取n=2,4,6时,分别估计了上述模型,得到的误差曲线如图5所示．从图中可以看出,3条曲线很难区分,表明参数维数对算法性能的影响不大．

4) 不同c时

分别取c=10%,30%和50%,使用本文算法对上述FIR模型参数进行了辨识,误差曲线如图6所示．由图6可见3条曲线的差别不大,表面所提的算法对不同添加的噪声有较好的抑制能力．

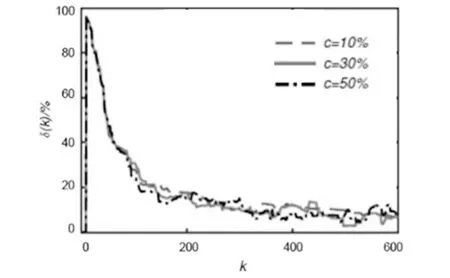
图6 不同c时的误差曲线

4 结束语

为了识别脉冲噪声扰动的FIR模型,提出了一种基于最小误差熵和峭度的可变步长SIG算法．基于该信息准则推导了随机信息梯度算法,该算法在脉冲噪声环境中给出参数向量的准确估计．为解决SIG算法收敛缓慢的问题,提出了一种基于峭度的可变步长SIG算法．为了实现该算法,基于大量数值仿真,给出了确定最大步长的简单公式．实验结果表明,对于脉冲噪声下的FIR模型,该算法能获得准确的估计,且具有较快的收敛速度．