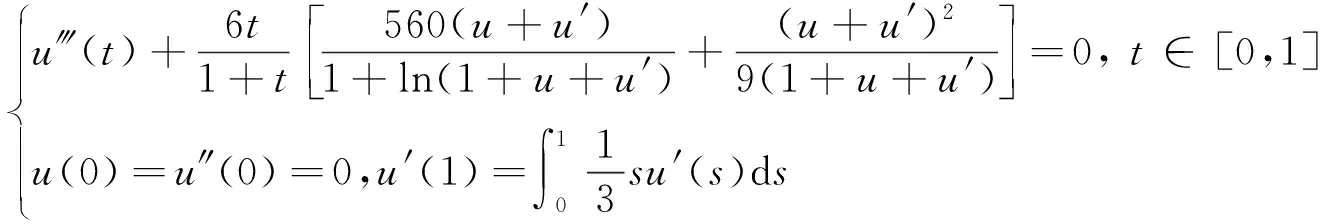一类三阶积分边值问题的正解
2022-06-17张广新杨赟瑞刘凯凯
张广新, 杨赟瑞 , 刘凯凯
(兰州交通大学 数理学院, 甘肃 兰州 730070)
0 引言
基于常微分积分边值问题在地下水流、等离子物理等领域的广泛应用,越来越多学者致力于此类问题正解的研究[1-4],并借助不动点定理、上下解方法结合极值原理、Leray-Schauder度理论等建立了一些有意义的研究成果,特别是偶数阶积分边值问题.
2011年,Ma[1]利用全局分歧方法结合Krein-Rutman定理研究了四阶积分边值问题
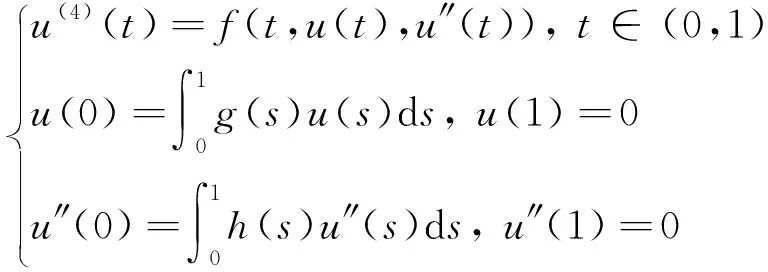
(1)
正解的存在性.
2020年,杨璐[2]基于Leggett-Williams不动点定理,研究了一类含双参数的四阶积分边值问题
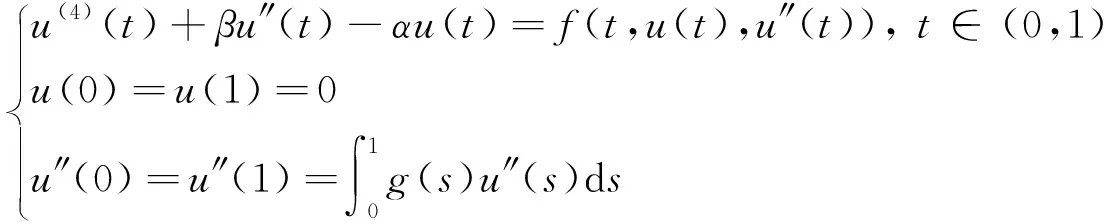
(2)
三个正解的存在性.但是,对奇数阶三阶积分边值问题正解的研究尚不多见[5-7].
2013年,杨佳[6]借助Guo-Krasnoselskill不动点定理研究了带积分边界条件的三阶边值问题
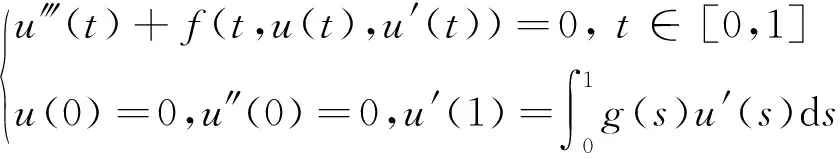
(3)
单调正解的存在性.
近来,何燕琴等人[7]利用混合单调算子方法建立了三阶积分边值问题
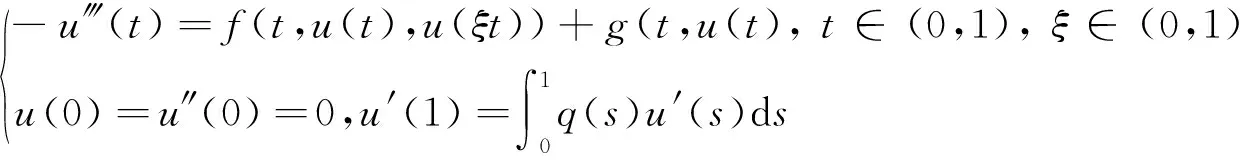
(4)
单调正解的存在性.
基于上述工作,本文利用Guo-Krasnoselskill不动点定理研究一类三阶积分边值问题
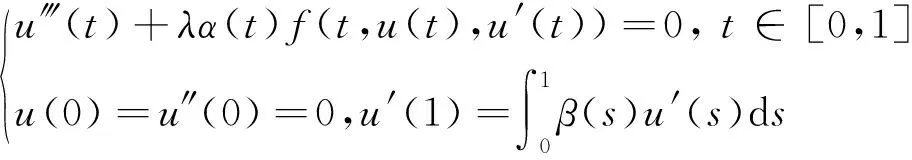
(5)
正解及两个正解的存在性.注意到,积分边值条件包含两点边值条件以及非局部条件.因此,本文完善并推广了一些三阶边值问题正解的研究结果[6,8].
1 预备知识
首先,给出本文需要的假设条件、相关定义和主要工具:
(A1)f∈C([0,1]×[0,+∞)×[0,+∞),[0,+∞));


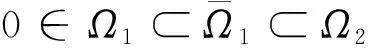
1)‖Tu‖≤‖u‖,u∈P∩∂Ω1,且‖Tu‖≥‖u‖,u∈P∩∂Ω2;
2)‖Tu‖≥‖u‖,u∈P∩∂Ω1,且‖Tu‖≤‖u‖,u∈P∩∂Ω2,
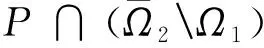
引理1 边值问题(5)有唯一解
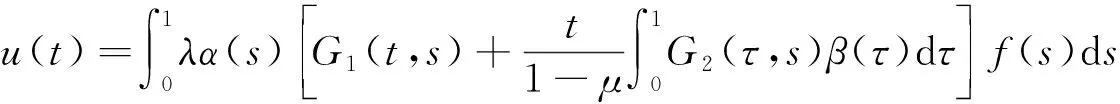
(6)
其中
证明过程类似于文[6],故此省略.
引理2Gi(t,s)(i=1,2)有以下性质:
(7)
(ii) 对∀t,s∈[0,1],有(1-t)(1-s)≤G2(t,s)≤1-s
(8)
(9)
证明(i) 当0≤s≤t≤1时,
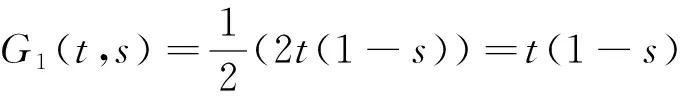
(ii) 不难验证,对任意的(t,s)∈[0,1]×[0,1],有(1-t)(1-s)≤G2(t,s)≤1-s成立.
记E=C1[0,1],对任意的u∈E,定义
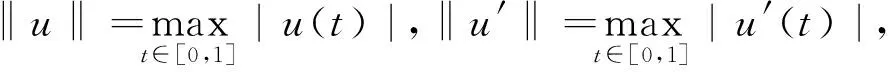
引理3 若(A1)~(A3)成立,则边值问题(5)的唯一解u满足u(t)≥0,u′(t)≥0,且

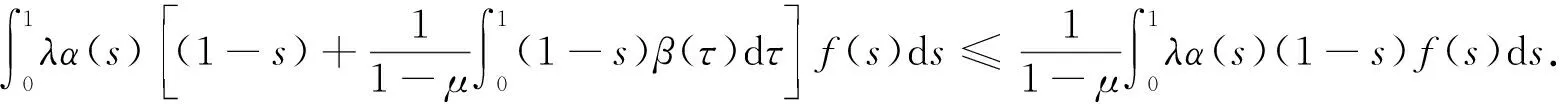
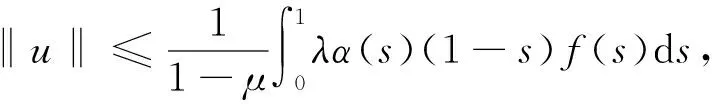
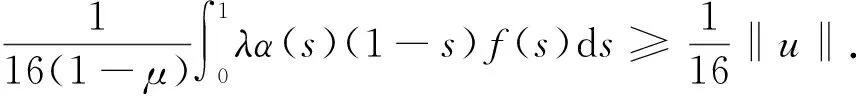
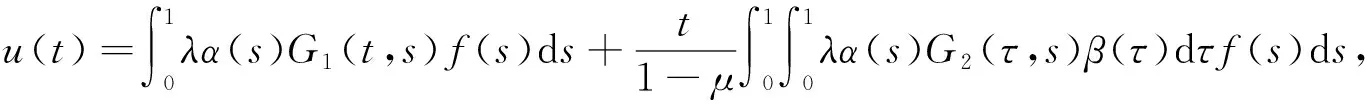
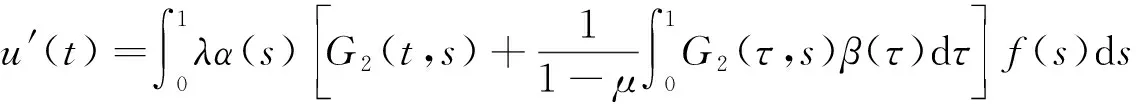
(10)
所以u′(t)≥0.由引理2可知,对任意的t∈[0,1],有

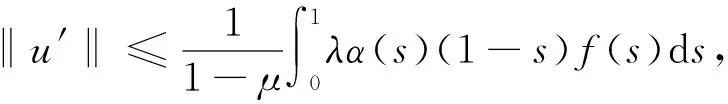
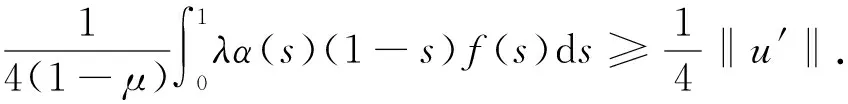
证毕.
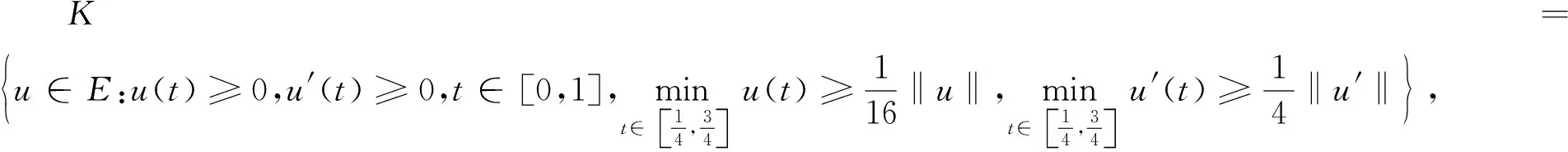
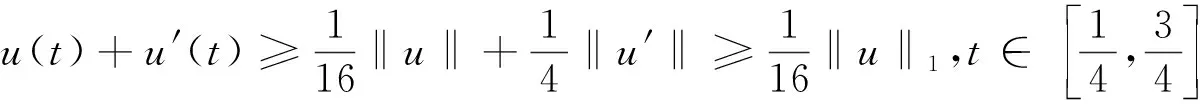
(11)
在K上定义算子T为
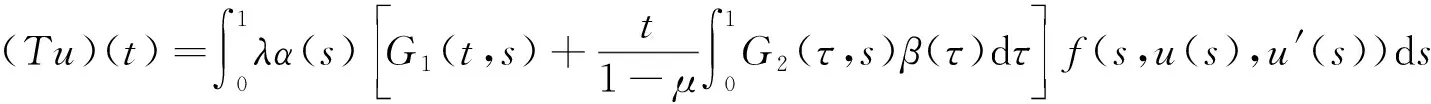
(12)
则边值问题(5)有解等价于算子T存在不动点.
引理4 若(A1)~(A3)成立,则T:K→K是全连续算子.
证明对任意的u∈K,有

(13)
因此(Tu)≥0,(Tu)′≥0.由式(12)、式(13)以及引理2知
和
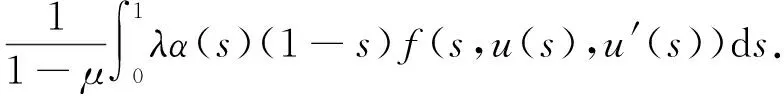
所以
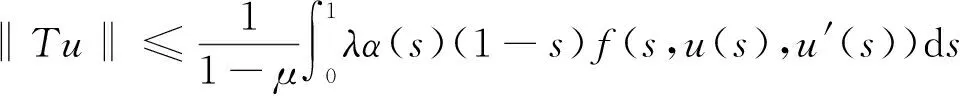
(14)
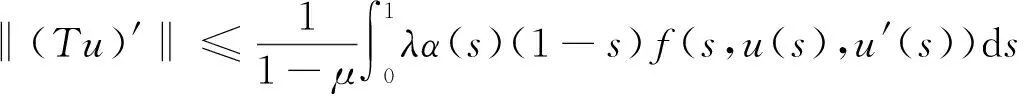
(15)
因此,结合式(12)~(15)及引理2,可得
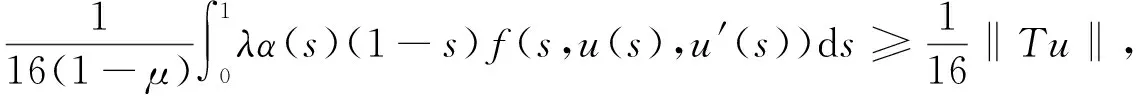
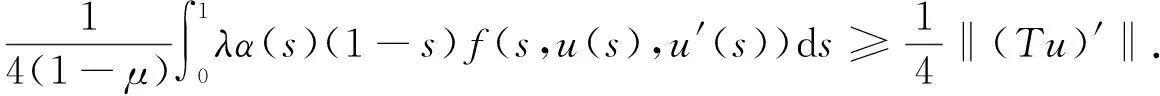
所以Tu∈K.
假设um,u∈k且‖um-u‖1→0(m→∞),则存在M1>0,使得对任意的自然数m,有‖um‖1≤M1.令
M2=sup{f(t,u,u′):(t,u,u′)∈[0,1]×[0,M1]×[0,M1]},
则对任意的t∈[0,1],由引理2可知,
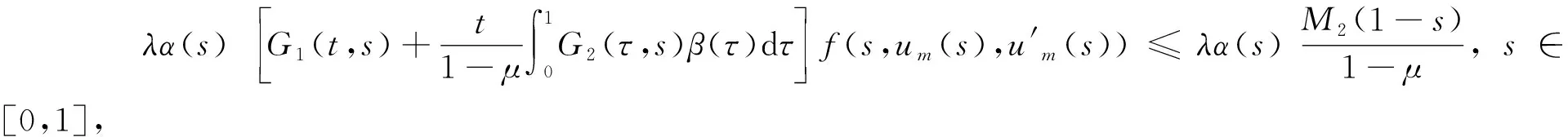

由勒贝格控制收敛定理可知,当t∈[0,1]时,有
和
从而
‖(Tum)-(Tu)‖1=‖(Tum)-(Tu)‖+‖(Tum)′-(Tu)′‖→0, (m→∞),
即T是连续算子.再利用Arzela-Ascoli定理不难证明T:K→K是全连续的.证毕.
2 主要结论
定义
定理2 若(A1)~(A3)成立,则边值问题(5)至少存在一个正解,当且仅当下列条件之一成立:
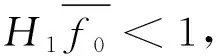
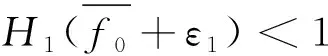
(16)
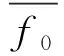
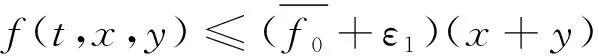
(17)
令Ω1={u∈E:‖u‖1<ρ1},则由式(17)可知,对任意u∈K∩∂Ω1,有
于是
同理可得
‖Tu‖1≤‖u‖1,u∈K∩∂Ω1
(18)

(19)
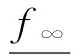
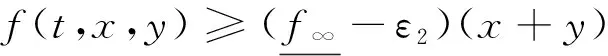
(20)
令ρ2≫ρ1,Ω2={u∈E:‖u‖1<ρ2},则由式(11)和式(20)可知,对于任意的u∈K∩∂Ω2,有
于是
同理可得
从而,由式(19)可知
即
‖Tu‖1≥‖u‖1,u∈K∩∂Ω2
(21)

(ii)的证明与(i)相似,故此省略.证毕.
定理3 若(A1)~(A3)和下述条件成立:
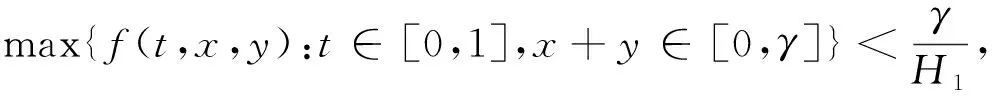
则边值问题(5)至少存在两个正解u1,u2,且满足0<‖u1‖1<γ<‖u2‖1.
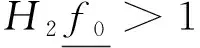
‖Tu‖1≥‖u‖1,u∈K∩∂Ωz
(22)
其中Ωz={u∈E:‖u‖1 ‖Tu‖1≥‖u‖1,u∈K∩∂Ωδ (23) 其中Ωδ={u∈E:‖u‖1<δ}. 记Ωγ={u∈E:‖u‖1<γ},则由条件(ii)可知,对任意的u∈K∩∂Ωγ,有 ‖Tu‖1=‖Tu‖+‖(Tu)′‖<γ=‖u‖1. 即 ‖Tu‖1<‖u‖1,u∈K∩∂Ωγ (24) 因此,由式(22)和式(24)及定理1可知,边值问题(5)存在正解u1,且z≤‖u1‖1<γ;同时,由式(23)和式(24)及定理1可知,边值问题(5)存在正解u2,且γ<‖u2‖1≤δ,故边值问题(5)至少存在两个正解u1,u2,且满足0<‖u1‖1<γ<‖u2‖1.证毕. 例1 考虑三阶积分边值问题 (25) 例2 考虑三阶积分边值问题 (26)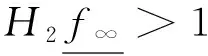
3 应用举例