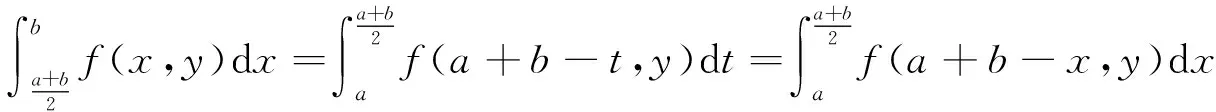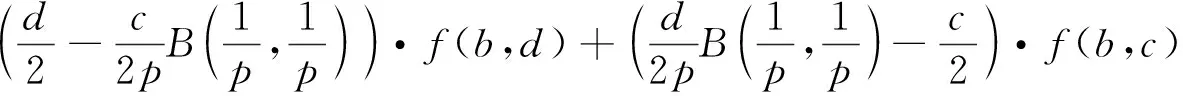一个二元p-凸函数的Hermite-Hadamard不等式
2022-06-17柏振宇柏传志
柏振宇, 柏传志
(1.江苏大学 数学科学学院, 江苏 镇江 212013; 2.淮阴师范学院 数学与统计学院, 江苏 淮安 223300)
0 引言
不等式在几乎所有数学分支中都是非常有用的工具.例如约束优化问题中的可行集就是用不等式表示的.不等式在自然科学以及数学的所有分支处理各种各样的问题中是不可或缺的工具.例如, 随机分析和概率中的切比雪夫和马尔可夫不等式[1],矩阵理论中的哈达玛不等式[2],控制理论中的李雅普诺夫不等式,经济学中经常用来处理均衡问题的变分不等式.
许多不等式的存在与凸性有关.集合的凸性的定义如下:
设X是实数域R上向量空间V上的一个集合.如果∀x,y∈X, ∀λ,μ∈R+,且λ+μ=1,有λx+μy∈X,则称X是一个凸集.
凸体(非空紧凸集)的几何性质导致了许多不等式的产生,如Brunn-Minkowski不等式和Blashcke-Santalo不等式,它们分别与两个凸体的和与积的体积有关.后来,凸性被扩展到具有不同运算的不同数学结构,如偏序集、格、度量空间.
设X是一个凸集,f:X→R.如果∀x,y∈X, ∀λ,μ∈R+且λ+μ=1,有
f(λx+μy)≤λf(x)+μf(y),
则称f是一个凸函数.
凸函数作为一类重要的函数,具有很多重要的性质,特别是在函数极值、数学规划、控制论等许多领域都有着广泛的应用.对于一元凸函数的性质和应用已经有非常广泛的研究[3-5].十九世纪末,Hermite 和 Hadamard在研究凸函数的性质时,分别独立地得到了下面的不等式.
若f:[a,b]→R是一个可积的凸函数,则
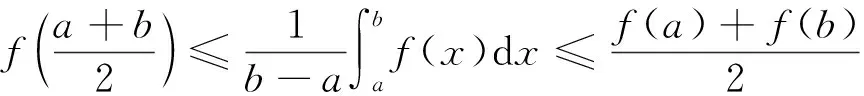
(1)
称为Hermite-Hadamard的不等式.函数凸性产生了大量不等式,Jensen不等式和Hermite-Hadamard不等式,都是基于凸性的最主要的两个不等式.
理论和应用的发展导致了一类新的凸性,如B-凸性,p-凸性等.许多作者研究了经典凸函数的多种不等式,并将其推广到新的凸类型.到目前为止,一元凸函数的Hermite-Hadamard不等式问题的研究,有着丰富的成果[6-7].本文将给出二元p-凸函数的Hermite-Hadamard型不等式.
1 预备知识和引理
多元凸函数的研究是近几十年形成和发展起来的一个新的数学分支,在数学规划和控制论等领域有着广泛的应用.
定义1[8]设D是R2上的一个凸集,函数f在D上有定义, 如果对于∀λ∈(0,1),∀(x1,x2),∀(y1,y2)∈D,有
f(λx1+(1-λ)y1,λx2+(1-λ)y2)≤λf(x1,x2)+(1-λ)f(y1,y2)
(2)
则称函数f为D上的凸函数.
注1n元凸函数可类似地定义.式(2)可推广到n元连续凸函数.
最近,文[9]给出并证明了特殊区域上的多元凸函数的Hermite-Hadamard不等式.
定理1(二元凸函数的Hermite-Hadamard不等式) 设函数f:[a,b]×[c,d]→R是二元连续凸函数, 则
(3)
文[10]给出了p-凸集与p-凸函数的概念,如下.
定义2[10]设U是Rn的一个子集及0 定义3[10]设U⊆Rn是一个p-凸集与f:U→R.如果∀t,s∈[0,1]且tp+sp=1,使得 f(tx+sy)≤tf(x)+sf(y), ∀x,y∈U. 则称f为p-凸函数. 为证明本文的一个结果,给出下面的定义. 定义4 对于 ∀(a1,b1),(a2,b2)∈R2, 如果a1≤a2,且b1≤b2,称(a1,b1)(a2,b2).对于f:R2→R, 如果 f(a1,b1)≥f(a2,b2), ∀(a1,b1)(a2,b2), 则称二元函数f是序减的.如果上式不等式反向,则称二元函数f是序增的. 最近, Eken[11]研究了p-凸函数的Hermite-Hadamard不等式, 推广了式(1).结果如下. 定理2[11]设f:[a,b]→R+是一个可积的p-凸函数.则 受文[9,11]的启发,本节将定理2推广到二元p-凸函数的情形. 下面,先给出一个引理. 引理1 设U⊆R2是一个p-凸集, 函数f:U→R且是一个二元p-凸函数,则 (i) 如果f关于第二变元是非增的,则对于固定的y0,F(x)=f(x,y0)是一元p-凸函数; (ii) 如果f关于第一变元是非增的,则对于固定的x0,G(y)=f(x0,y)是一元p-凸函数. 证明证(i), (ii)类似可证.任取x1,x2,使得z1(x1,y0),z2(x2,y0)∈U,∀t,s∈[0,1]且tp+sp=1,有 f(tz1+sz2)≤tf(z1)+sf(z2), 即 f(tx1+sx2,(s+t)y0)≤tf(x1,y0)+sf(x2,y0). 因为t+s≤tp+sp=1,而f关于第二变元是非增的,故 f(tx1+sx2,y0)≤f(tx1+sx2,(s+t)y0). 于是,由上两式,得 F(tx1+sx2)≤tF(x1)+sF(x2). 结论成立. 性质1[11]对于a>0,[0,a)是一个p-凸集. 定义beta函数为 有关其性质, 参见文[12]. 定理3 设f:[a,b]×[c,d]→R+是一个可积的p-凸函数,如果f是序减的,则 A1f(a,c)+A2f(a,d)+A3f(b,c)+A4f(b,d) (4) 其中b>a≥0,d>c≥0,且 证明先证明式(4)的左边.因为f为二元p-凸函数, 故 (5) 因为 (6) 令t=a+b-x,则 (7) 故由式(5)~(7),得 (8) 又因为 (9) 令t=c+d-y,则 (10) 于是再由式(5), 及式(8)~(10),得 下面,证明式(4)的右边.作变量代换 于是 (11) 根据引理1, 有 (12) 将式(12)代入式(11), 得 (13) 再作变量代换 根据引理1,得 (14) 同理,有 (15) 将式(14)与(15)代入式(13), 得 定理4 设f:[a,b]×[c,d]→R+是一个可积的p-凸函数.令 则 (i) 如果f是一个二元序减函数,那么g是一个二元p-凸函数; 证明(i) 对∀w1(t1,s1),w2(t2,s2)∈[0,1]×[0,1],λ,μ≥0且λp+μp=1.则有 (16) 其中 根据条件f是可积的p-凸函数, 且是序减的,以及λ+μ≤1,有 (17) 将式(17)代入式(16),得 g(λw1+μw2)≤λg(w1)+μg(w2). (ii)令 于是 (18) 其中 应用p-凸函数的Hermite-Hadamard不等式(4)的左边,可得 注3 定理4是文[11]中定理3.9的推广.
2 主要结果