对尺规作图的再理解

摘要：关于尺规作图的教学在我们的课堂中应该怎么教，教到什么程度，值得我们思考，以2021年福建省一道中考试题为例，阐述尺规作图的基本思路、操作流程与原理分析，对教学的实践进行思考，引导关注几何教学，发展学生核心素养.

关键词：尺规作图;几何教学;初中数学

中图分类号：G632文献标识码：A文章编号：1008-0333（2022）14-0026-03

收稿日期：2022-02-15

作者简介：林龙海（1977.8-），男，福建省福州长乐人，本科，中学一级教师，从事初中数学教学研究.

尺规作图是初中数学几何教学中的一块重要内容，隶属于几何与图形板块，中考对尺规作图的考查常常涉及多种方式，试题往往以不同的形式呈现，但无论何种形式，了解作图的基本过程、理解作图的基本原理、掌握作图的基本技能与方法是解决问题的关键所在.

1 对尺规作图的知识应用再理解

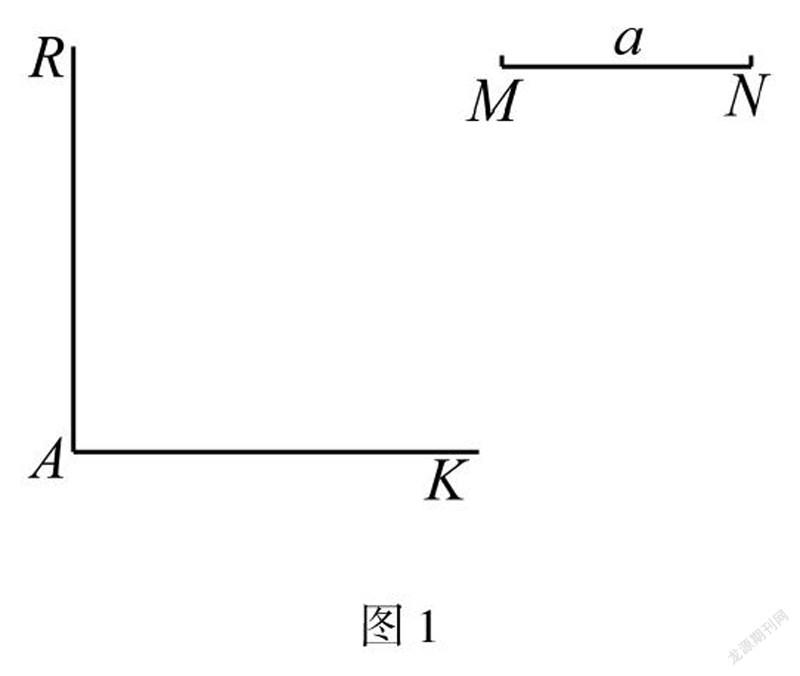
（2021·福建）如图1，已知线段MN=a，AR⊥AK，垂足为A.

（1）求作四边形ABCD，使得点B，D分别在射线AK，AR上，且AB=BC=a，∠ABC=60°，CD∥AB;（要求：尺规作图，不写作法，保留作图痕迹）

（2）略.

1.1 试题分析

本题的作图并没有明确指明使用哪一种基本作图方式，属于基本作图的应用，需要学生根据题意来选择怎样的基本作图操作来实现求解.此类试题的解决在于首先要明确几何图形的基本性质，然后根据其基本性质，使用几个基本的尺规作图进行叠加或组合完成.

1.2 解法分析

下面给出10种不同的解法，从不同角度、不同方式来重新认识一下尺规作图.

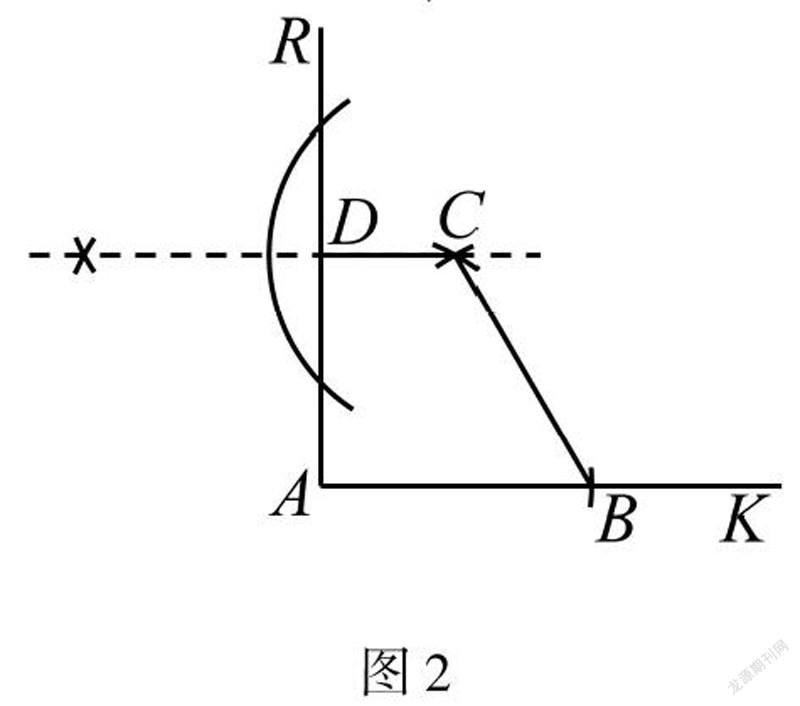
解法1作垂线得到点D

如图2，使用“作一条线段等于已知线段”，以点A为圆心，a为半径画弧，在射线AK上作AB=a，作出点B，再次使用这个基本作图，作出等边三角形ABC，再过点C作CD⊥AR，垂足为点D，得到点D.

分析看到60°想到等边三角形，看到AR⊥AK想到作垂线得出CD∥AB.解法1使用2种基本作图得到答案.

解法2作菱形得到点D

如图3，同解法1得到点B和点C，再分别以点A，C为圆心，a为半径画弧，两弧交于点E，得到菱形ABCE或菱形ABEC，直线CE与AR交点即为点D.

分析看到60°想到等边三角形，为了得到CD∥AB，想到菱形的性质：对边平行，作菱形出平行.解法2使用5次同一种基本作图得到答案.

解法3作菱形得到点D

如图4，同解法2得到点E，再以点C为圆心，a为半径画弧，交AR于点F，得到菱形ACFE，菱形ACFE的对角线CE与AF的交点即为点D.

分析看到60°想到等边三角形，看到AR⊥AK为了得出CD∥AB，故利用菱形的性质：对角线互相垂直，作点D.

解法4作一个角等于已知角得到点D

如图5，同解法1得到点B和点C，在点C处利用“作一个角等于已知角”得到∠DCE=∠ABC，直线CD与AR的交点即为点D.

分析看到60°想到等边三角形，为了得到CD//AB想到了平行线的性质：同位角相等，两直线平行，作同位角相等得到答案.

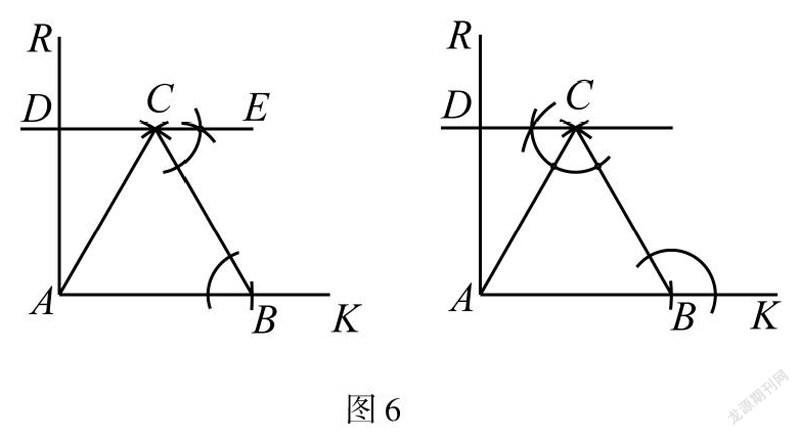
解法5作一个角等于已知角得到点D

如图6，同解法1得到点B和点C，在点C处再用“作一个角等于已知角”，作出∠BCE=∠ABC或∠DCB=∠CBK，直线CD与AR的交点即为点D.

分析看到60°想到等边三角形，为了得到CD∥AB想到了平行线的性质：内错角相等，两直线平行，作内错角相等得到答案.

解法6作线段垂直平分线，作一个角等于已知角得到点D

如图7，同解法1得到点B和点C，“作线段AB 的垂直平分线”，过点C作CE⊥AB于点E，得到AE=BE，用“作一个角等于已知角”，过点E作∠AED=∠ABC，得到△AED≌△EBC，ED∥BC，利用全等的对应边相等，得到ED=BC，故四边形EBCD是平行四边形，CD∥AB.

分析看到60°想到等边三角形，为得到CD∥AB故作出平行四边形，由平行四边形的对边平行，得到答案.使用了3种基本作图得到答案.

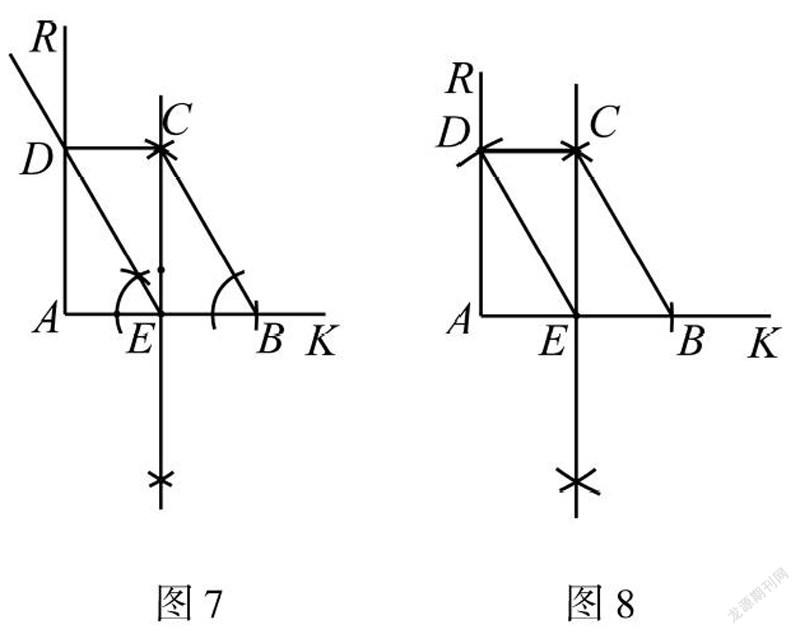
解法7作线段垂直平分线，作一条线段等于已知线段得到点D

如图8，同解法1得到点B和点C，再作线段AB 的垂直平分线得到点E，过点E作ED=BC，作点D.

分析看到60°想到等边三角形，为了得到CD//AB，利用AR⊥AK想到作矩形，利用矩形的对边平行.

解法8作线段垂直平分线，过一点作已知直线的垂线得到点C

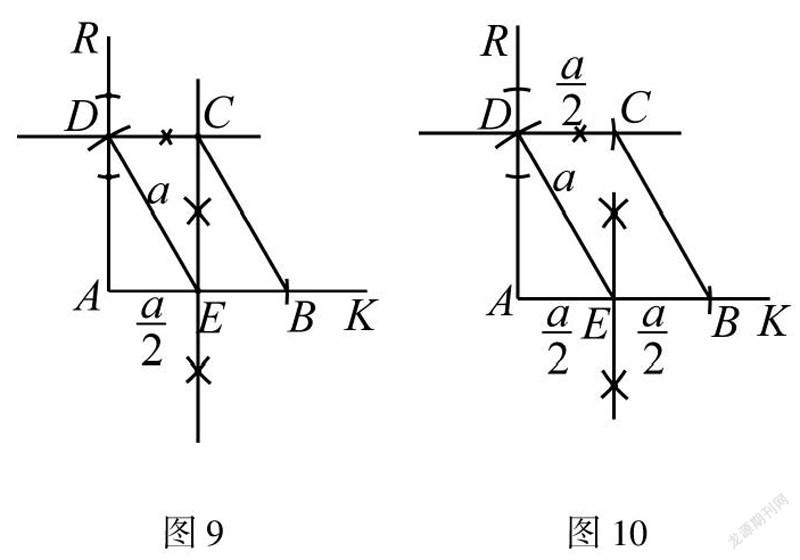
如图9，同解法1得到点B，作线段AB的垂直平分线交AB于点E，过点E作ED=AB，得到△AED为含30°的直角三角形，作点D，过点D作AR的垂线交线段AB的垂直平分线于点C.

分析看到60°，AR⊥AK想到含30°的直角三角形，为了得到CD∥AB，作CD⊥AR.使用了3种基本作图得到答案.

解法9作线段垂直平分线，过一点作已知直线的垂线得到点C

如图10，同解法8得到点D，过点D作AR的垂线，再过点D作DC=AE，得到点C.

分析看到60°，AR⊥AK想到含30°的直角三角形，為了得到CD∥AB，作CD⊥AR，利用DC=AE得到点C.

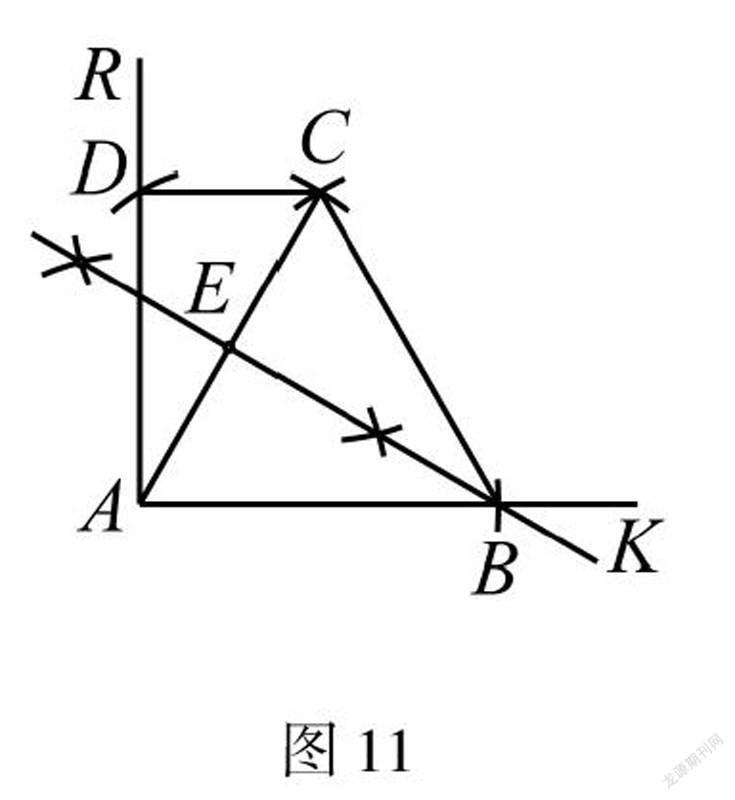
解法10作线段垂直平分线得到点D

如图11，同解法1得到点B和点C，作线段AC 的垂直平分线交AC于点E，再以点E为圆心，EC为半径画弧，交AR于点D，作点D.

分析看到60°想到等边三角形，为了得到CD∥AB，看到AR⊥AK想到去得到∠ADC=90°，利用直径所对的圆角为90°，得到答案.

上述10种解法，大多采用1种多次使用或2种或3种基本的尺规作图组合完成，依据几何性质，找到相应的基本作图，产生出不同的解法.

2 对尺规作图的教学意义再理解

2.1 在尺规作图教学中，可以利用一题多解与多解归一方式培养核心素养

本题内涵丰富，解法多样，多种解法都能回归到最基本的尺规作图，教学中对每一种解题方法给出逻辑思考，让学生在历练基本作图的基础上，知法明理，结合直觉思维与逻辑推理，在动脑、动手的学习中培养学生的数学思维，形成良好的直觉思维和几何直观等核心素养.

2.2 在尺规作图教学中，可以利用逆向思维方式培养探究意识

尺规作图不仅是一种操作，更是对数学思维和探究的一种过程，一种溯源过程.教师在教学中，要引导学生先自行独立思考，尝试各种解法，洞察学情，以学定教.

2.3 在尺规作图教学中，可以利用经典著作与故事渗透中国传统文化的教育

尺规作图是数学文化长廊中的不可多得的耀眼明珠，广大数学爱好者围绕着它，产生了许多有趣的数学问题，利用经典著作与故事，可以更好地传播数学文化，在操作与求证过程中，能深刻体会到尺规作图彰显了数学独特的文化魅力.

参考文献：

[1] 周建勋.无锡市中考尺规作图题的命制及思考[J].中学数学月刊，2014（11）：43-45.

[2] 章飞.三个基本作图的方法思辨与教学实施[J].中学数学教学参考（中旬），2021（7）：2-4.

[3] 顾香才.一道尺规作图题的多种作法与教学启示[J].中学数学教学参考（中旬），2020（4）：40-42.

[4] 刘芳.对尺规作图教学的三个思考[J].初中数学教与学，2010（2）：27-29.

[责任编辑：李璟]