浅析情境教学法在数学教学中的应用

张滨

[摘  要] 一直以来，情境教学法深受广大教育工作者的喜爱. 这种教学方法可避免传统教学方式的单一性，对调动学生的学习兴趣，激发探究欲具有显著的促进作用. 文章从三方面谈一些拙浅的看法：新奇情境，激发探究兴趣;现实情境，解决实际问题;实验情境，自主建构新知.

[关键词] 情境;兴趣;问题;探究

情境教学法是指教师在教学中有意识地创设或引入一些生动具体或带有感情色彩的场景，让学生在情境体验中激发情感，从而更好地理解所学内容. 这种教学方法最早于1930年由英国语言学家提出，主要是将一些生活或社会现象经加工提炼后，寓教于具体情境中，对学生学习产生直接或间接的影响. 真实、情深意长是它的主要特征，学生在丰富的情境中能获得知情意行的统一.

新奇情境，激发探究兴趣

众所周知，兴趣能有效地提高学生学习的积极主动性，使得学生在学习中获得学习的成就感与满足感. 但兴趣并非是人与生俱来的，需要教师通过一定的教学手段润物细无声地进行渗透，让学生在不知不觉中产生学科兴趣. 创设新奇的教学情境就是激发学生兴趣常用的教学手段之一，教师以丰富有趣的内容吸引学生的目光，能让学生全身心地投入到问题的探究中.

学习机制学说提出学习的发生一般都起源于情境，尤其是新奇的情境会触发学生的好奇心，推动学生产生求知的本能. 因此，教师在情境创设时可结合学生认知结构的发展水平，以趣味横生的教学情境来刺激学生的感知系统，使学生对教学内容保持长久的兴趣与探究的欲望.

案例1  “轴对称”的教学.

这是一个相对而言比较重要，却又有点抽象的内容. 为了激发学生的探究欲，笔者以“将军饮马”的小故事进行课堂导入，让学生在这个奇特的故事中感知“对称”对生活的影响.

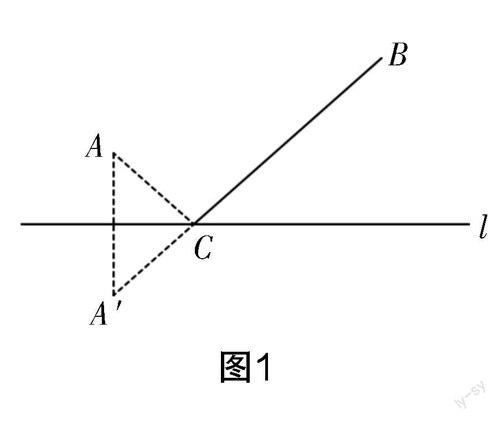
情境：古希腊不仅有我们耳熟能详的神话故事，还有丰富的历史故事. 相传在两千多年前，一位机智勇猛的大将军提出一个奇怪的问题让部下去研究.如图1所示，假设我们在点A处（草地）将马喂饱之后，准备再牵着马去河边（直线l）饮水，待马儿吃饱喝足后将马牵回营地（点B处），整个过程怎么走，路程最短？

将领们对这个问题是百思不得其解，直到数学家海伦提出解决问题的办法，大家才恍然大悟，这就是历史著名的“将军饮马”问题，此问题一直沿用至今. 聪明的同学们，你们有办法来解答这个经典问题吗？

学生都被这个精彩、新奇的故事所吸引，一个个都积极开动脑筋，跃跃欲试. 有学生提出可尝试运用物理学中的“镜面成像”来解决问题，也有学生提出要寻找一个新的点C等.

眼看此情境已经成功地激起了学生的探究兴趣，笔者则趁热打铁，利用多媒体的动画演示功能向学生展示了探究点C的过程. 此时，那些原本猜测得差不多的学生一个个都表现出兴奋、激动的表情，成就感不言而喻. 而拥有其他想法的同学，在直观的多媒体演示中也产生了直观形象的认知体验，很快就形成了情感上知情意行的统一.

一个短小的历史故事，点燃了所有学生的探究热情. 在学生自主猜想的基础上揭晓答案的方式，使得猜对的学生产生了满满的成就感，同时也获得了其他学生情感上的认同，有效地促进了学习动机的形成. 因此，新奇的情境对激趣与引发探究欲具有重要影响.

现实情境，解决实际问题

弗赖登塔尔提出：“数学与生活有着密切的联系，它源自生活又应用于生活. ”现代心理学研究证明，与生活经验有联系的学习材料能有效地激起学生的探究欲. 因此，数学教学可从学生的生活出发，创设与学生生活经验相契合的情境，以揭示数学概念或方法的发生发展历程，让学生从中感悟相应的数学思想，形成良好的数学思维品质.

案例2  “二次函数”的概念教学.

学习这个概念之前，学校刚组织过三人篮球赛的活动. 因此，笔者将此活动作为情境创设的材料，让学生在运球、投篮所行走的路线中感知二次函数. 在此基础上，再引入学生所熟悉的正方形面积与边长相对应关系的变化规律问题. 随着几个生活材料的引入，学生在教师的引导下，逐渐体会到关系式之间的联系、曲线的存在等数学问题.

同时，笔者还引入表格让学生填写，鼓励学生通过表格的观察，发现各个量之间的内在关系，从而找出相应的函数关系式，体会这些变化与一次函数有怎样的区别. 课堂随着生活情境的深入，学生在教师的点拨下，获得y=ax2+bx+c（a≠0）的二次函数关系式.

为了深化知识的内涵，笔者鼓励学生将此关系式与之前接触过的“一元二次方程”进行比较，从它们的异同点中感知各自的特点. 如此，学生从生活材料中提炼出二次函数，也体验到二次函数与其他知识的异同点. 在情境的帮助下，学生自主揭开抽象的二次函数的面纱，使得学习过程异常轻松、愉快.

创设生活情境值得注意的是，材料必须是在学生认知范围内的，最好是学生有着切身体会的内容，如此能快速调动学生参与的积极性，让学生在材料的观察、分析与类比等中推导、提炼出相应的概念与规律. 除此之外，教师还可反过来，引导学生将知识应用于所创设的现实情境中，以提高学生的灵活应用能力.

案例3  “二次函数”的应用.

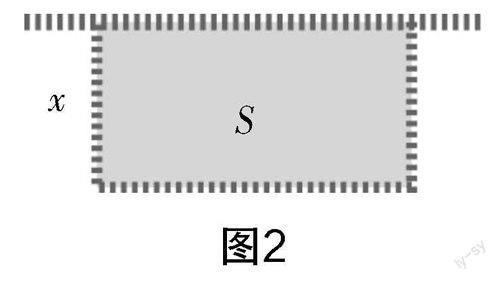
问题：如圖2所示，李伯伯准备用50 m长的篱笆在一堵墙墙边围出一个长方形的小菜园，你能写出小菜园的面积S（m2）与宽x（m）之间存在的函数关系式吗？该菜园的长与宽分别为多少时，面积最大？

从题意看，该菜园的长为（50-2x），S与x之间的函数关系式为S=x·（50-2x）. 分析可知当x的值为12.5时，该小菜园的面积最大（过程略）.

这是将二次函数运用到生活实际中的情境，学生通过该情境的分析与思考，对二次函数的应用价值有了更为深刻的理解. 学生在知识的活学活用中形成了良好的解题能力，为数学核心素养的形成与发展夯实了基础.

实验情境，自主建构新知

杜威的“在做中学”的理念对数学教学产生了深远的影响. 随着新课改的推进，这种教学方法越来越受关注. 平时教师用得比较多的就是创设实验情境，让学生在动手操作中感知、体验并领悟问题的发生与解决过程，从而自主建构新知.

学生在实验情境的体验过程中，手、口、眼、耳、脑等各个感官系统都会参与活动过程. 整个过程不仅有丰富的语言作为基础，还有图文结合的支持. 学生在直观形象的实验观察中衍生出良好的逻辑思维能力，为深刻理解并掌握新知提供了保障.

案例4  “菱形的性质”的教学.

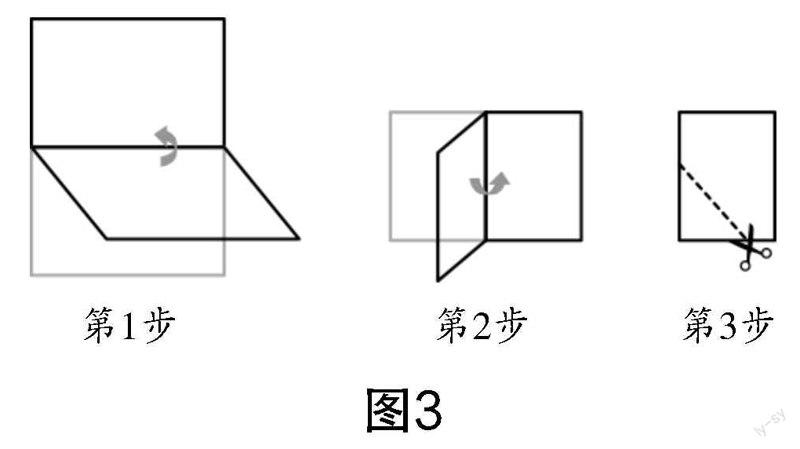
（1）如图3所示，取一张A4纸，纵横各对折一次，沿着虚线剪下并展开.

（2）独立思考，观察展开后图形的角、边、线以及对称性，提出看法.

（3）小组合作学习. 思考以下几个问题：①从展开图的边来观察，其位置与数量有什么特殊的关系？②观察展开图的角，思考其邻角与对角之间具备怎样的特殊关系. ③观察展开四边形的对角线，它们具有怎样的关系？④被对角线分割后形成的角之间具有怎样的特点？⑤思考该图形是不是轴对称图形. 若是，对称轴在哪儿？有几条？它们之间的位置关系是怎样的？

随着活动的深入，学生在亲自动手操作中独立思考，并在小组合作交流中探讨教师提出的各个问题. 整个过程民主、和谐，教师对学生的合情推理给予充分的肯定，以鼓励学生大胆地猜想，最后各组总结汇报问题的答案. 不知不觉，本节课的教学重点与难点任务，就在实验情境中得以有效完成.

总之，情境教学法在当前初中数学课堂中应用得较为广泛. 教师不论选择哪种形式的情境，其目的都在于激发学生的探究欲，为学生提供新颖、丰富的学习环境，优化课堂结构的同时更好地完成教学任务. 除了上述几种方法之外，教师还可根据实际情况创设开放、拓展的情境，让学生产生更多的情感体验，为建构与完善知识体系奠定基础.