基于加权平均随机递归梯度下降算法
2022-05-20费经泰郝庆一程一元
费经泰,郝庆一,程一元,孙 钊
(1.巢湖学院 数学与统计学院,安徽 巢湖 238024;2.安庆师范大学 数理学院,安徽 安庆 246133;3.安徽建筑大学 数理学院,合肥 230601)
0 引 言
在大规模机器学习问题中,常常考虑如下的优化问题[1]:
(1)
其中,n表示样本的数目,d表示样本的维度,每个分量函数fi是凸的,并且具有连续的Lipschitz梯度。这里假定ω*是问题(1)的最优解。
对于问题(1),传统的方法采用的是确定性梯度下降算法(GD)[2],GD算法的迭代公式如下:
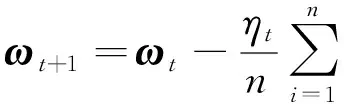
其中,ηt表示学习率。可以看到每迭代一次要计算全部样本的梯度,故计算的复杂度较高,所以后续学者提出了随机梯度下降算法(SGD)[3],迭代公式如下:
ωt+1=ωt-ηt∇fit(ωt)
SGD算法每次只选取一个样本进行迭代,因此计算量大大减少,并且随机梯度是真实梯度的无偏估计,即E[∇fit(ωt)]=∇F(ωt)。但随着迭代的进行,SGD算法所产生的方差也在不断加大。因此即使在强凸条件下也仅具有次线性的收敛速度。[4-6]
为了克服上述问题,2013年,Johnson[7]提出了方差缩减梯度下降算法(SVRG),该算法采用正则化的随机梯度,迭代公式如下:

它仍是真实梯度的无偏估计,即E[vt]=∇F(ωt)。并且文献[7]证明了随着迭代进行,方差在不断地减小,从而在强凸条件下能够达到线性收敛速率,因此得到广泛应用。此后有学者相继提出一些改进或者相似的方差缩减类算法,具有代表性的有随机平均梯度算法(SAG)[8],该算法每轮随机选择一个样本计算梯度,其他样本的梯度保持不变,最后再将整个样本的梯度进行平均来更新参数值。随机加速平均梯度下降算法(SAGA)[9]将SAG算法中的梯度替换思想和SVRG的方差缩减思想相结合,从而在强凸条件下收敛速度更快些。但SAG算法和SAGA算法需要用一张梯度表来储存每个样本的梯度,故占用内存比较大。2017年,Nguyen[10]提出了随机递归梯度下降算法(SARAH),该算法在更新梯度的过程中使用了递归方法,所以不需要对梯度进行保存,并且在迭代的过程当中方差也在减小,因此也是有效的方差缩减算法。
本文在传统的SARAH算法基础上,提出了一种基于加权平均思想的方差缩减算法—WA-SARAH算法,证明了该算法在强凸条件下具有线性收敛速率,并且得到了更好的收敛阶,最后在经典机器学习数据集上,算法的实验结果表现良好。
1 SARAH算法和WA-SARAH算法
本节先介绍传统的SARAH算法,算法的流程如下:

算法1 SARAH算法输入:初始向量ω0,内循环数m,学习率η1:for s=1,2,…,do2: ω0=ω~s-13: v0=1n∑ni=1儊fi(ω0)4: ω1=ω0-ηv05: for t=1,…m-1,do6: 随机选择一个样本it7: vt=儊fit(ωt)-儊fit(ωt-1)+vt-18: ωt+1=ωt-ηvt9: end for10: ω~s=ωt; t从0,1,2,…,m 随机选取11:end for
SARAH算法采取的是两层循环迭代,外层循环计算样本的全梯度,内层循环计算正则化的随机梯度。不同于经典的方差缩减梯度下降算法(SVRG),SARAH算法的内层循环中随机梯度采取的是递归地更新方式,它是最优下降方向的有偏估计,即
E[vt]=∇F(ωt)-∇F(ωt-1)+vt-1≠∇F(ωt)
现对上述算法进行推广,提出一种基于加权平均随机递归梯度下降算法(WA-SARAH),具体见算法2。从算法2中可以看到SARAH算法是WA-SARAH算法的一种特殊情形。

算法2 WA-SARAH算法输入:初始向量ω0,内循环数m,学习率η1:for s=1,2,…,do2: ω0=ω~s-13: v0=1n∑ni=1儊fi(ω0)4: ω1=ω0-ηv05: for t=1,…m-1,do6: 随机选择一个样本it7: vt=p儊fit(ωt)-儊fit(ωt-1) +vt-18: ωt+1=ωt-ηvt9: end for10: ω~s=ωt; t从0,1,2,…,m 随机选取11:end for
对WA-SARAH算法中第7行中的vt的更新方式
vt=p[∇fit(ωt)-∇fit(ωt-1)]+vt-1
(2)
重新进行改写,得到如下:
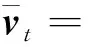
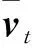
2 WA-SARAH算法收敛性分析
本节将给出WA-SARAH算法的收敛性分析,为此先给出相关的假设和引理。
假设1:(L-光滑).每个fi:Rd→R,i=1,2,…n是L-光滑的,即对任意的ω,ω′∈Rd,存在常数L>0,使得
‖∇fi(ω)-∇fi(ω′)‖≤L‖ω-ω′‖
假设2:(μ-强凸).函数F:Rd→R是μ-强凸的,即对任意的ω,ω′∈Rd,存在常数μ>0,使得
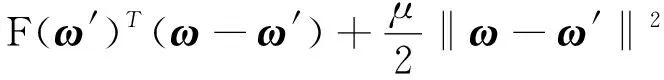
假设3:每个fi:Rd→R,i=1,2,…n是凸的,即对任意的ω,ω′∈Rd,有
fi(ω)≥fi(ω′)+∇fi(ω′)T(ω-ω′)
引理1[2]:如果F是凸函数并且L-光滑,则对任意的ω,ω′∈Rd,有
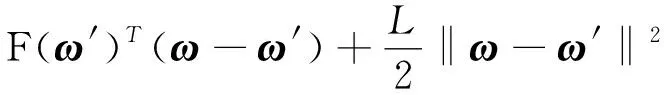
(3)
2L[F(ω)-F(ω*)]≥‖∇F(ω)‖2
(4)
(5)
引理2[2]如果F是强凸函数,则对任意的ω∈Rd,有
2μ[F(ω)-F(ω*)]≤‖∇F(ω)‖2
(6)
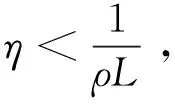
证明由ωt+1=ωt-ηvt,有
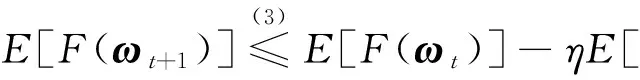

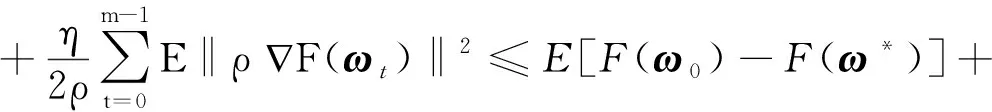
引理4在假设1的条件下,根据WA-SARAH算法,对∀t≥1,有
证明E‖ρ∇F(ωj)-vj‖2=
E‖[ρ∇F(ωj-1)-vj-1]+[ρ∇F(ωj)-ρ∇F(ωj-1)]-[vj-vj-1]‖2=
‖ρ∇F(ωj-1)-vj-1‖2+‖ρ∇F(ωj)-ρ∇F(ωj-1)‖2+E‖vj-vj-1‖2+
2ρ(ρ∇F(ωj-1)-vj-1)T(∇F(ωj)-∇F(ωj-1))-
2(ρ∇F(ωj-1)-vj-1)TE[vj-vj-1]-
2ρ(∇F(ωj)-∇F(ωj-1))TE[vj-vj-1]=
‖ρ∇F(ωj-1)-vj-1‖2-ρ2‖∇F(ωj)-∇F(ωj-1)‖2+E‖vj-vj-1‖2
(7)
其中
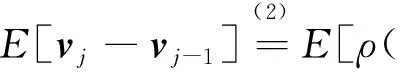
注意∇F(ω0)=v0,则‖ρ∇F(ω0)-v0‖2=(ρ-1)2‖v0‖2。(7)式两边对j=1,2,…,t相加并取期望得
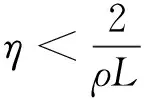
证明对于∀j≥1,有
E‖vj‖2=E‖vj-1-ρ(∇fij(ωj-1)-∇fij(ωj))‖2=
上式两边对j=1,2,…,t相加得
(8)
由引理4可得
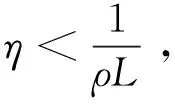
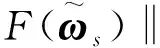
其中合理地选择ρ,η和m,使得
证明由引理5可得
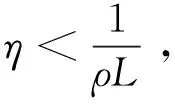
根据F的强凸性,结合∇F(ω0)=v0可得
迭代可得
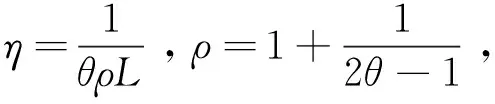
3 数值实验和结果讨论
下面通过数值实验来验证算法的效率,这里采用标准的机器学习数据集:Mnist数据集和合成logistic回归数据集(Synthetic logistic data)。其中Mnist数据集中训练集样本数n=6 000,维度d=784,测试集样本数n=1 000。logistic回归数据集中训练集样本数n=10 000,维度d=100,测试集样本数n=3 000。采用的机器学习回归任务是带L2正则项的logistic回归:
其中,(xi,yi)为给定样本数据,λ是正则化参数,F(ω)是一个强凸光滑的损失函数。
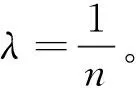

(a) synthetic data训练集下收敛速率 (b) minist data训练集下收敛速率图1 不同加权系数ρ下收敛速率对比图
图2表示不同随机梯度下降算法(SGD,SVRG,SAGA,SARAH,WA-SARAH)在训练集下收敛速率对比图。从图中可以看到SAGA算法在训练集下收敛速度稍快一些,但该算法所占内存较大。SGD算法和SVRG算法在迭代前期效果比SARAH算法和WA-SARAH算法好一些,但到了迭代后期,SARAH算法和WA-SARAH算法下降地更快些,即更加逼近最优解。
图3为在不同测试集下,不同算法在当前迭代下错误率对比图。随着迭代地进行,最终可以看到SAGA算法的错误率比其他算法要低些,其次是WA-SARAH算法和SARAH算法,SGD和SVRG的错误率要相对高一点。从而说明本文所提算法的有效性。
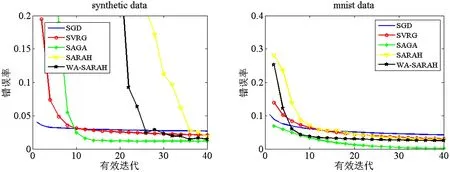
(a) synthetic data测试集下错误率 (b) minist data测试集下错误率图3 不同算法在不同测试集下错误率对比图
