Virtually正则模

王永铎, 刘世杰

(兰州理工大学 理学院, 甘肃 兰州 730050)

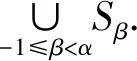
定义1称模M是virtually正则的,如果M的每个有限生成子模同构于M的直和项.称模M是完全virtually正则的,若M的任意子模是virtually正则的.称M是半完全virtually正则的,若M的每个有限生成子模是virtually正则的.

例11)zZ是virtually正则的,但不是正则的.

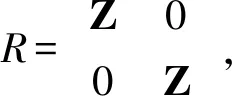
下面的例子说明virtually正则模的商模和直和项不一定是virtually正则的.

例21)zZ是virtually正则的,而Z/4Z不是.

证明由文献 [2]中的例2.7可知M是virtually半单模,则M是virtually正则的.而Z/4Z的有限生成子模2Z/4Z到Z/4Z的任意直和项都不能建立同构.

命题1设M是virtually正则模.若M=M1⊕M2是M的一个分解且有Hom(M1,M2)=0,则M2是virtually正则模.

证明对M2的任意有限生成子模K,由M是virtually正则模知K≅N使得M=N⊕N′.由Hom(M1,M2)=0及文献[5]中的引理1.9知M1是M的完全不变子模,则M∩M1=(N⊕N′)∩M1=(N∩M1)⊕(N′∩M1).由Hom(M1,N)=0(若Hom(M1,M2)≠0,则有非零同态f:M1→N≅K→M2与Hom(M1,M2)=0矛盾)知N∩M1=0(如果有非零元x∈N∩M1,则M1→N∩M1→N非零),则M1≤N′,N′=M1⊕(N′∩M2),即M=N⊕M1⊕(N′∩M2)=M1⊕M2.故M2≅N⊕(N′∩M2),所以N同构于M2的直和项,即M2是virtually正则模.

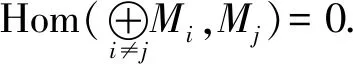
证明以n=2为例,其余类推可证.

⟹ 对M的任意有限生成子模N,由T=R1⊗R2知TN=e1N⊕e2N,其中(e1,0),(0,e2)是T的中心正交幂等元(e1R2=e2R1=0且e1+e2=1T).eiN(i=1,2)是Mi的有限生成子模,由RiMi是virtually正则模知eiN≅Ki≤⊕Mi(i=1,2).则N≅K1⊕K2≤⊕M.

⟸ 设T=R1⊗R2.则T-模M=e1M⊕e2M,其中(e1,0),(0,e2)是T的中心正交幂等元.显然eiM(i=1,2)是Ri-模也是T-模.则Hom(Mi,Mj)=0(i≠j).(若有非零映射f:0≠e1m1∈Te1M→e2m2∈Te2M),则有f((1,0)·e1m1)=f(e1m1)=e2m2≠0,而(1,0)f(e1m1)=(1,0)e2m2=0).由命题1可知Mi是virtually正则模.

命题2设R是环,M是左R-模.则以下几条成立.

1) 设I是R的理想且IM=0.则M是virtually正则的R/I-模当且仅当M是virtually正则的R-模.

2) 若M是virtually正则的,则M的每个有限生成子模是M的同态像.若M的每个有限生成子模是M投射的,反之也成立.

3) (完全)virtually正则模有Morita不变性.

4) 若M是virtually正则模,W是M的有限生成子模且包含M的可嵌入到W的所有子模,则W是virtually正则模且存在K≤⊕M使得K≅W,M=K⊕K′.特别的,若W是Dedekind有限的.则W≤⊕M.

证明1) 由文献 [9]中的定理1.2.8(3)可知.

2) ⟹ 由virtually正则模的定义可知M的每个有限生成子模N同构于M的直和项,即N是M的同态像.

⟸ 已知对M的任意有限生成子模N,均有满态射f:M→N→0.由N是M投射的可知f是可裂的,即N同构于M的直和项.

3) 由Morita等价保持有限生成,单态射以及直和项可知.

4) 由M是virtually正则模,W是M的有限生成子模可知W≅K≤⊕M.又K⊆W,则K≤⊕W.类似地,对任意有限生成的N≤W≤M均有N≅V≤⊕M.又V≅N⊆W.则V⊆W,V≤⊕W.故W是virtually正则模,若W是Dedekind有限的,则W=K⊕K′≅W⊕K′,K′=0,则W=K≤⊕M.

命题3设R是环,M是左R-模.则以下两条成立.

1) 若M是virtually正则的,Z(M)是有限生成戴德金有限的,则M=W⊕L,其中W是奇异virtually正则模,L是非奇异virtually正则模.

2) 若Soc(M)是有限生成模,则M是有限生成的virtually正则模当且仅当M≅W⊕L,其中W是有限生成半单模,L是有限生成的virtually正则模且Soc(L)=0.

证明1) 对任意N≤M,若有单射f:N→Z(M),则N≅Imf≤Z(M).由Imf是奇异的可知N是奇异的,则N≤Z(M).由命题2中4)可知M=Z(M)⊕L.其中L是M的非奇异子模,Z(M)是virtually正则的.若W≅Z(M),则M≅W⊕L,Hom(W,L)=0.由命题1知L是virtually正则模.

2) ⟹ 对任意N≤M,若有单射f:N→Soc(M),则N≅Imf≤Soc(M).由Imf是半单的可知N是半单的,则N≤Soc(M).由Soc(M)是有限生成的半单模知Soc(M)的每个其次分量是有限生成的.根据文献[2]中的命题2.5知Soc(M)是戴德金有限的.由命题2中4)可知M=Soc(M)⊕L且Hom(Soc(M),L)=0.由命题1与有限生成模的直和项是有限生成的知L是有限生成的virtually正则模且Soc(L)=0(若Soc(L)≠0,则有极小子模K≤L≤M,因此K是M的极小子模,这与M=Soc(M)⊕L矛盾).

命题4诺特模M是virtually正则的当且仅当M是virtually半单的.

证明⟹ 由文献[10]中的命题1.5知，诺特模的每个子模是有限生成的,又因为M是virtually正则的,所以M的每个子模同构于M的直和项,即M是virtually半单的.

⟸ 由定义可知.

命题5设M是模.则下列两条等价：

1)M是virtually正则模.

2) 对于每个有限生成子模N≤M,均有M的幂等自同态f使得f(M)≅N.

证明由文献[11]中的推论5.8知，M的每个直和项是M的幂等自同态像,M的每个幂等自同态像是M的直和项,根据virtually正则模的定义即证.

命题6有限直内射模M是virtually正则模当且仅当M是正则的.

证明根据定义可知正则模显然是virtually正则模.由M是virtually正则模知,对M的任意有限生成子模N均同构于M的直和项.因为M是有限直内射模,所以N是M的直和项,即M是正则的.

推论3满足C2条件的模M是virtually正则模当且仅当M是正则的.

定义2称环R是左virtually正则环,如果RR是virtually正则模.称环R是左强virtually正则环,如果RR的每个有限生成子模是virtually正则模.

注1左强virtually正则环是左virtually正则环,但是左virtually正则环不一定是左强virtually正则环.

定理1设R为环.则下列条件等价：

1)R是左强virtually正则环.

2) 每个有限生成的自由左R-模是左半完全virtually正则的.

3) 每个自由左R-模是左半完全virtually正则的.

4) 每个投射左R-模是左半完全virtually正则的.

3)⟹4) 对任意投射左R-模的有限生成子模P,由投射模是自由模的直和项知P必是某个自由模的子模,又每个自由左R-模是左半完全virtually正则的,则P是virtually正则的,即每个投射左R-模是左半完全virtually正则的.

4)⟹1) 由环R作为左R-模是投射模可知,RR是左半完全virtually正则的,即R是左强virtually正则环.

推论4环R是左virtually正则的当且仅当每个(有限生成)自由左R-模是virtually正则的.

证明⟸ 由R作为左R-模是自由模可知R作为左R-模是virtually正则的,即环R是左virtually正则的.

命题71) 设环R与S是Morita等价的.则R是左强virtually正则环当且仅当S是左强virtually正则环.

2) 左virtually正则环关于有限直积是封闭的.

证明1) 因为投射模,有限生成子模,virtually正则模均具有Morita不变性,则由推论4可证.

2) 推论2中取Ri=R,Mi=R(1≤i≤n)可知.