探究线段和最小值问题的一般解法

广东省广州市广东广雅中学(510800)林碧珠

1 预备知识

1.1 线段公理

两点之间,线段最短.

1.2 垂线段最短

过直线外一点与直线上各点连接的所有线段中,垂线段最短.

2 模型原型

2.1 异侧两点

如图1,点A,B分别是直线l异侧的两个点,如何在l上找到一个点C,使得点C到点A、点B的距离的和最短?

图1

根据线段公理,不难得出,如图2,连接AB,与直线l交于点C,点C即为所求.

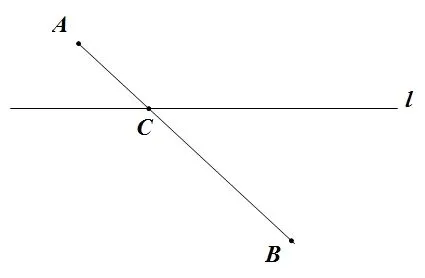
图2

2.2 同侧两点(将军饮马)

如图3,牧马人从A地出发,到一条笔直的河边l 饮马,然后到B地.牧马人到河边什么地方饮马,可使所走的路径最短?

图3

【分析】如图4,作出点B关于l的对称点B′,将同侧两点转为异侧,利用轴对称的性质,可以得到CB′=CB.这样,问题转化为: 当C在l的什么位置时,AC与CB′的和最小?

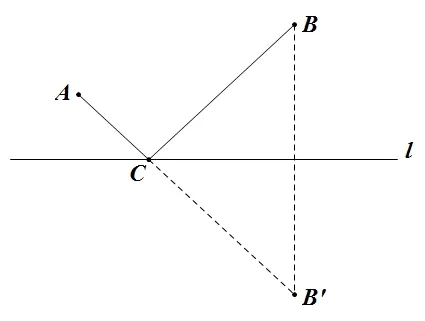
图4

在连接A,B′两定点的路径中,由线段公理可得,线段AB′最短.因此,线段AB′与直线l的交点C的位置即为所求.

【思路】

①找出定点: 点A,点B;动点: 点C(在直线l上运动,则l为对称轴).

②找出求和中的特殊线段(指由一个定点和一个动点组成的线段):CA,CB.

③求和中含有同一个动点(点C)的两条线段CA和CB在对称轴l的同侧.

④作特殊线段中定点关于动点所在直线(即对称轴)的对称点,如: 作点B关于l的对称点B′,将CB转为CB′,此时AC,CB′在对称轴的异侧,再连接AB′,由线段公理,AB′的长度即为AC+CB的最小值,且AB′与l的交点即为所求的点C.

3 模型使用的难点与关键点

模型的原型对学生而言,难度不大,但只要稍加变式、复杂化,多几个点或多几条线,学生就分不清应该作哪个点关于哪条线的对称点,不知道如何化折为直,确定最短路径.

4 通过特例,找出一般规律

对求和中的线段所包含的点分为定点和动点,下面分别探究“两定一动”型、“两定两动”型和“一定两动”型,并总结出解决此类问题的一般规律.

4.1 “两定一动”型

如图5,在菱形ABCD中,AB=2a,E在BC上,BE=a,∠BAD=120°,点P在BD上,求线段PE+PC的最小值.

图5

【分析】

①定点:C,E;动点:P(在BD上).

②特殊线段:PE,PC.

③PE,PC在对称轴BD同侧,如图6,由菱形的性质可知,点C关于BD的对称点为点A,则PE+PC=PE+PA,即求点P在BD上运动的过程中,PE+PA的最小值.由线段公理,显然,在连接A,E两定点的路径中,线段AE最短,为.

图6

4.2 “两定两动”型

如图7,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA上,求MP+PQ+QN的最小值.

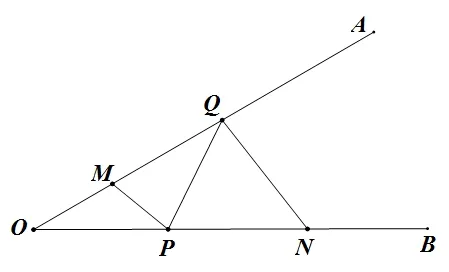
图7

【分析】

①定点:M,N;动点:P(在OB上),Q(在OA上).

②特殊线段:MP,QN.

③MP,PQ在对称轴OB同侧,如图8,作特殊线段MP中定点M关于OB的对称点M′;QN,PQ在对称轴OA同侧,作特殊线段QN中定点N关于OA的对称点N′.

图8

④MP+PQ+QN=M′P+PQ+QN′,即求连接M′,N′两定点的路径长的最小值,由线段公理,显然连接M′N′,M′N′的长度即为最小值,通过计算,为.

4.3 “一定两动”型

如图9,点P在∠AOB内部,试在OA、OB上分别找出两点E、F,使ΔPEF周长最短.

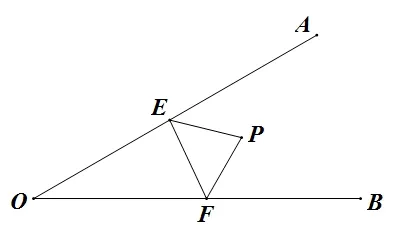
图9

【分析】ΔPEF的周长为:PE+EF+PF

①定点:P;动点:E(在OA上),F(在OB上).

②特殊线段:PE,PF.

③PE,EF在对称轴OA同侧,如图10,作特殊线段PE中定点P关于OA的对称点P′;EF,PF在对称轴OB同侧,作特殊线段PF中定点P关于OB的对称点P′′

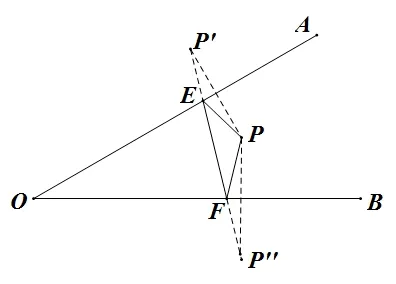
图10

④PE+EF+PF=P′E+EF+P′′F,即要使连接P′,P′′两定点的路径长取得最小值,由线段公理,显然连接P′P′′,分别与OA、OB交于点E、F,此时,ΔPEF周长最短.

4.4 规律总结

①找出定点,动点和对称轴(即动点运动所在直线)

②找出求和中的特殊线段(指由一个定点和一个动点组成的线段)

③判断求和中所有含有同一个动点的两条线段在对称轴的同侧还是异侧.若异侧,则直接连接线段;若同侧,则作特殊线段中定点关于动点所在直线(即对称轴)的对称点,将所有的同侧转为异侧,再连接对称点

④由线段公理,连接对称点的线段的长度即为求和的最小值,且该线段与对称轴的交点即为所求的动点的位置.

5 链接中考

【2020年广州中考第24 题】 如图11,⊙O为等边ΔABC的外接圆,半径为2,点D在劣弧AB上运动(不与点A,B重合),连接DA,DB,DC.若点M,N分别在线段CA,CB上运动(不含端点),经过探究发现,点D运动到每一个确定的位置,ΔDMN的周长有最小值t,随着点D的运动,t的值会发生变化,求所有t值中的最大值.

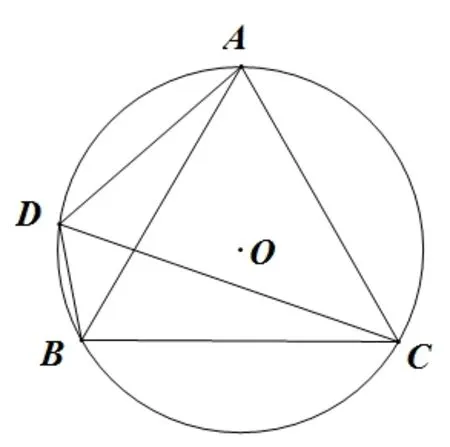
图11

【分析】ΔDMN的周长为:DM+MN+DN

①定点:D(每一个确定的位置);动点:M(在CA上),N(在CB上).

②特殊线段:DM,DN.

③DM,MN在对称轴CA同侧,如图12,作特殊线段DM中定点D关于CA的对称点D′;MN,DN在对称轴CB同侧,作特殊线段DN中定点D关于CB的对称点D′′

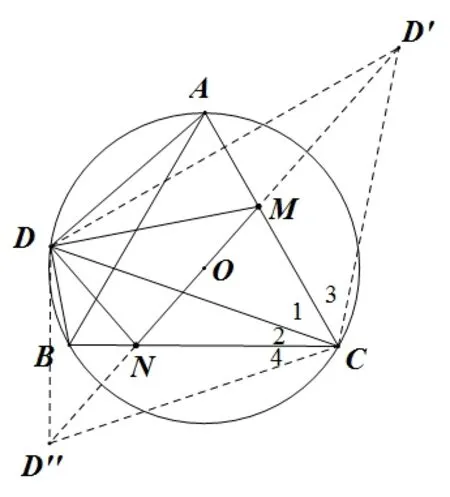
图12

④DM+MN+DN=D′M+MN+D′′N,即要使连接D′,D′′两定点的路径取得最小值,由线段公理,显然连接D′D′′,分别与CA、CB交于点M、N,此时,ΔDMN周长最短,为D′D′′的长度.

由轴对称的性质可得,CD′=CD,CD′′=CD,∠1=∠3,∠2=∠4,又因为∠1+∠2=60°,所以∠D′CD′′=120°,因此D′D′′是顶角为120°的等腰ΔD′CD′′的底边,不难计算.随着点D的运动,CD的长度也会发生改变,当CD的长度取得最大值时,t取得最大值,不难发现当CD为直径时,CD取得最大值,为4,因此t的最大值为.

2.【2018年广州中考第23 题】如图13,在四边形ABCD中,∠B=∠C=90°,AB ＞CD,AD=AB+CD.

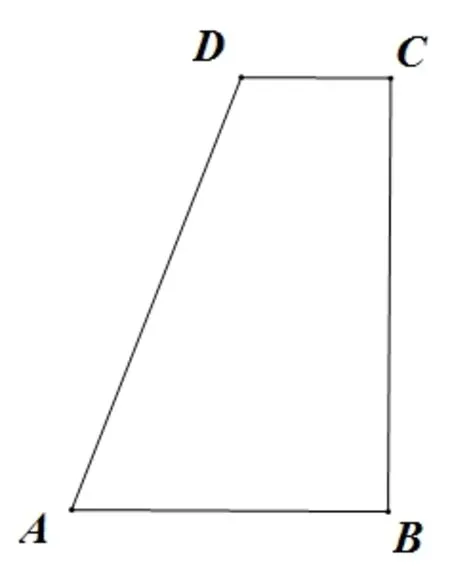
图13

(1)利用尺规作∠ADC的平分线DE,交BC于点E,连接AE(保留作图痕迹,不写作法)

(2)在(1)的条件下,

①证明:AE⊥DE;

②若CD=2,AB=4,点M,N分别是AE,AB上的动点,求BM+MN的最小值.

【分析】第(1)问略,第(2)问中的①略.

(2)②

1°定点:B;动点:M(在AE上),N(在AB上).

2°特殊线段:BM.

3° BM,MN在对称轴AE同侧,由①知,AE平分∠DAB,则如图14,作特殊线段BM中定点B关于AE的对称点B′落在AD上.

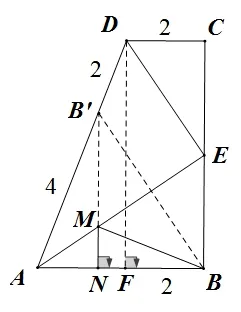
图14

4° BM+MN=B′M+MN,即要使连接定点B′和动点N的路径取得最小值,由线段公理和垂线段最短可知,过点B′作AB的垂线段,垂线段即为最短路径,设垂足为N,此时,BM+MN有最小值,为B′N的长度.

过点D作DF⊥AB于点F,则B′N//DF.由①可知,BF=DC=DB′=2,AB=AB′=4.因为AB′:B′D=AN:NF,所以4 : 2=AN:(2-AN),解得的最小值为.由勾股定理得,,即BM+MN

3.【2021年天津中考第25 题】已知抛物线y=ax2-2ax+c(a,c为常数,a ／=0)经过点C(0,-1),顶点为D.

(Ⅰ)当a=1 时,求该抛物线的顶点坐标;

(ⅠⅠ)当a ＞0 时,点E(0,1+a),若,求该抛物线的解析式;

(ⅠⅠⅠ)当a ＜-1 时,点F(0,1-a),过点C作直线l平行于x轴,M(m,0)是x轴上的动点,N(m+3,-1)是直线l上的动点.当a为何值时,FM+DN的最小值为并求此时点M,N的坐标.

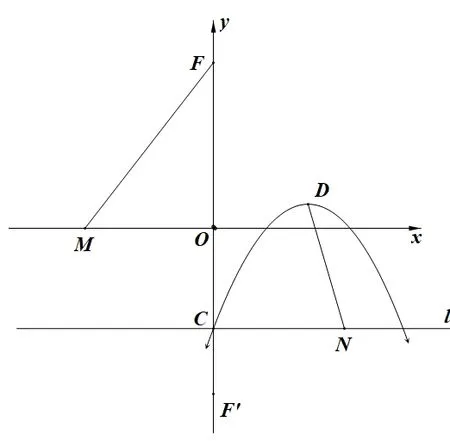
图15

【分析】第(Ⅰ),(ⅠⅠ)问略.

(ⅠⅠⅠ)FM和DN是两条没有公共交点的线段,M点和N点都是动点,但这两个动点之间有关联,只要确定了其中一个点的坐标,另一个点就确定了,因为N点的横坐标比M点的横坐标多3,N点的纵坐标比M点的纵坐标少1.要使FM和DN这两条求和线段有公共交点,不难发现,如图16,只要将N点向左平移3 个单位长度,再向上平移1 个单位长度,得到的N′点就与M点重合.将D点作同样的操作,得到D′点,连接D′M,此时DN就被平移到了D′M的位置,FM+DN=FM+D′M.下面分析怎么找到FM+D′M的最小值(将军饮马模型).

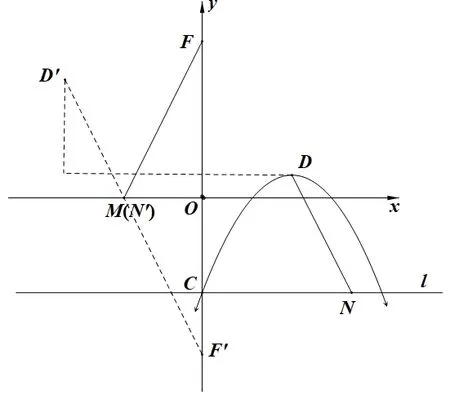
图16

①定点:D′(-2,-a)和F(0,1-a);动点:M(m,0)(在x轴上).

②特殊线段:FM,D′M.

③FM,D′M在对称轴x轴同侧,作特殊线段FM中定点F关于x轴的对称点F′(0,a-1).FM+D′M=F′M+D′M,即要使连接定点F′和定点D′的路径长取得最小值,由线段公理可知,连接D′F′,线段D′F′即为最短路径,设D′F′与x轴交于点M,此时的点M刚好能使FM+DN取得最小值,FM+DN=FM+D′M=F′M+D′M=D′F′.