探求特殊四边形中线段和的最小值

左效平 崔成进

探求线段和的最小值问题是中考的重要考点. 这类问题背景丰富，现举例说明.

正方形背景下探求线段和的最小值

【构建模型】 在正方形中，一动点 + 两定点，对称点在形上，探求线段和的最小值.

【解答要领】 确定对称点：根据正方形的对称性，对称点就是对角线的两个顶点;确定线段和取最小值时动点的位置：对称点和另一定点的连线与动点所在直线的交点;确定与线段和相等的最短线段：对称点与另一定点构成的线段.

例1 如图1，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD + PE的和最小，则这个最小值为（ ）.

A.  2[3] B.  2[6] C.  3 D.  [6]

解析：如图2，∵正方形ABCD是轴对称图形，且点B，D是对称点，

设AC与BE交于点P，连接PD，此时PD + PE最小，∴PD + PE = PB + PE = BE，

∵正方形ABCD的面积为12，∴AB = [23]，∴BE = AB = [23]. 故应选A.

【同步演练】 如图3，正方形ABCD的边长是4，M在DC上，且DM = 1，N是AC边上一动点，则△DMN周长的最小值是 .

菱形背景下探求線段和的最小值

【构建模型】 在菱形中，一动点 + 两定点，对称点在形上，探求线段和的最小值.

【解答要领】 确定对称点：根据菱形的对称性，对称点就是对角线的两个顶点;确定线段和的值时，动点的位置：对称点与另一定点的连线与动点所在直线的交点;确定与线段和相等的最短线段：对称点与另一定点构成的线段.

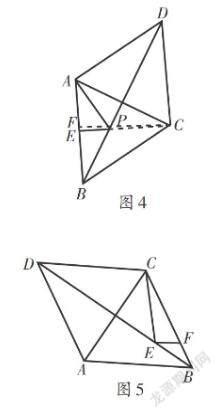
例2 已知菱形ABCD的周长为16，面积为8[3]， E为AB的中点，若P为对角线BD上一动点，则EP + AP的最小值为 .

解析：如图4，菱形ABCD是轴对称图形，且点A，C是对称点，

连接CE，交BD于点P，此时EP + AP最小，

EP + AP = EP + PC = EC，

∵菱形ABCD的周长为16，∴其边长为4，

过C作CF⊥AB，垂足为F，

∵菱形ABCD的面积为8[3]，∴CF = 2[3]，∴BF = [42-（23）2] = 2，

∴点E为AB的中点，∴点F与点E重合，

∴CE = 2[3]，∴EP + AP的最小值为2[3]. 故应填2[3].

【同步演练】 如图5，在边长为6的菱形ABCD中，∠ABC = 60°，E，F分别是BD，BC上的动点，则CE + EF的最小值为 .

矩形背景下探求线段和的最小值

【构建模型】 在矩形中，一动点 + 两定点，对称点在形外，探求线段和的最小值.

【解答要领】 确定对称轴：动点所在直线;构造对称点;构造与所求线段和相等的最短线段：对称点与另一定点构成的线段.

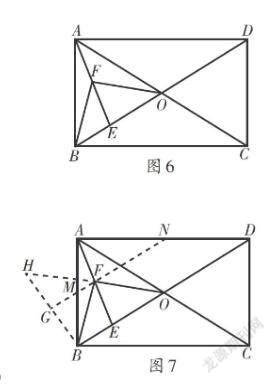
例3 如图6，在矩形ABCD中，AB = 4，对角线AC，BD交于点O，∠AOD = 120°，E为BD上任意点，F为AE的中点，则FO + FB的最小值为（ ）.

A. 2[7]       B. 2 + [3]     C. 5     D. 3[3]

解析：如图7，过AB的中点M和AD的中点N作线段MN，

∵F为AE的中点，∴MF[⫽]BE，FN[⫽]ED，

∴M，F，N三点共线，即点F在线段MN上，

作点B关于MN的对称点H，连接BH，与NM的延长线交于点G，

连接FH，则BH⊥NG，FB = HF，∴FB + FO = HF + FO，

其最小值应为OH的长，即点F为OH与MN的交点.

∵∠AOD = 120°，∴∠AOB = 60°，

∵四边形ABCD为矩形，∴OA = OB，∴△OAB为等边三角形，

∴OB = AB = 4，∠ABO = 60°，∵NG[⫽]BD，∴∠HBO = ∠HGF = 90°，

∴∠MBG = 30°，MB = 2，∴MG = 1，∴GB = [3]，∴HB = 2GB = 2[3]，

在Rt△HBO中，HO = [BO2+HB2] = [42+（23）2] = 2[7]. 故选A.

【同步演练】 在矩形ABCD中，AB = 2，AD = 3，E，F分别是AD，CD上的动点，EF = 2，Q是EF的中点，P为BC上的动点，连接AP，PQ，则AP + PQ的最小值等于（ ）.

A. 2 B. 3 C. 4 D. 5

同步演练答案：1. 6（提示：连接BM交AC于N'.） 2. 过点A作AF⊥CB，垂足为F，交BD于E，CE + EF最小值为3[3]. 3. C（提示：作点A关于BC的对称点A'，连接A'P，DQ，当A'，P，Q，D在同一直线上时，AP + PQ的最小值等于A'D - DQ的长.）