联结历史与现实,沟通数学与人文*——以初中“函数的概念”教学为例

上海市新杨中学(200331)李德虎

华东师范大学数学科学学院(200241)余庆纯

1 引言

基于数学史的数学文化,是指基于数学史阐释数学的思想、精神、语言、方法、观点及其演进过程,还包括数学在人类生活、科学技术、社会发展等方面的贡献与意义;其主要分为知识源流、学科联系、社会角色、审美娱乐与多元文化五个维度[1].研究表明,基于数学史的数学文化课例教学,沟通了历史与现实、数学与人文两座桥梁,有效地改善HPM 实践中“高评价、低运用”的教学困境.

函数概念是数学学科大概念(big ideas)之一,其指向培育数学学科核心素养的关键内容知识与思想方法,贯穿初、高中数学课程的学习,是描述客观世界中变量关系与变化规律的数学语言与工具.初中“函数的概念”是沪教版数学教科书八年级上册第18 章第1 节的内容,主要通过实例学习变量、常量、函数等相关概念,领会函数的意义,初步感知函数的表示方法[2].《上海市中小学数学课程标准》指出: 通过身边事例与生活实例,具体认识变量以及变量之间的相依关系,展示函数概念的形成过程,体会函数的意义[3].可见,初中“函数的概念”是从常量过渡到变量、初步建构函数概念的启蒙课,引导学生形成动态的数学观,为后续学习正比例函数、反比例函数、一次函数、二次函数等内容以及高中阶段不同类型的函数、数列、导数等内容打下认知的基础.

教材方面,通过对现行的沪教版、人教版、北师大版教科书的比较,发现三个版本的教科书对“函数概念”的内涵界定、引例内容等方面存在异同(见表1)[2][4-5].首先,不同版本的教科书对于“函数概念”的内涵界定存在差异: 沪教版教科书介绍“变量依赖关系”的函数概念,而人教版、北师大版的教科书则阐述“变量对应关系”的函数概念.其次,在“函数概念”的引例内容上,普遍引用实际生活实例,突出“数学来源于生活,服务于生活”的本质.其中,沪教版的教科书基于问题情境,引出学习长度、面积、体积、质量、温度、时间、速度等常见的数量;再通过“环绕地球飞行的同心圆”问题,引入常量、变量的概念;

表1 “函数的概念”在不同版本教科书中的比较

接着以“汽车行驶的路程x(千米)与油箱里剩余的油量y(升)之间的变化关系”引出函数的概念.人教版教科书则通过圆的面积、人口统计图等实例,解析函数的概念.北师大版教科书通过高度与时间、层数与总数等实例引入函数的概念.

函数是培育数学抽象、逻辑推理、数学建模等数学核心素养的必要抓手.一线教学实践发现,三版教科书的引例内容普遍没有回答清楚学习函数概念的必要性,且依据前期调查,学生对函数概念的理解存在一定的认知困难.

鉴于此,本研究通过梳理“函数概念”相关的数学史,分析其蕴含的数学文化内涵维度并运用于课堂教学中,旨在追寻数学家们的火热思考,建构历史与现实、数学与人文两座桥梁,引导学生突破函数概念学习的认知障碍,加深对函数概念本质的理解,回答清楚函数概念学习的必要性,进一步揭示数学史的教育价值,感悟数学文化之魅.因此,拟定初中“函数的概念”教学目标如下:

(1)通过“滴滴打车”计费、“嫦娥一号”飞行等现实问题,初步理解变量、常量的概念; 基于“石子计数”、“鸡兔同笼”、“炮弹轨迹”等数学史料的问题情境,初步感知、抽象出函数的概念;通过回顾函数概念的历史演变过程,感悟变化过程中两个变量之间存在的确定关系,理解“变量依赖关系”的函数定义,了解“变量对应关系”的函数定义,培养动态的数学观;

(2)通过微视频、趣味漫画和交流讨论等形式,了解欧拉、狄利克雷等数学家在不同时期的函数定义,感悟函数演变的数学本质,理解“函数”中文译名的来源,体会在函数概念演变中呈现的多元数学文化,培育批判求实的理性精神.

2 史料运用

在历史长河中,人类对“函数”的感知由来已久.早在古希腊时期,毕达哥拉斯学派常常借助小石子来计数或演示不同类型的“形数”,建立了一种事物计数的有效方式.曾经在一场古代战争中,几个部队的士兵不断地聚集前往战场,为了解士兵参战的情况,指挥官要求每位参战的战士兵留下一个石子,这样通过计算石子的数量得到参战的士兵数量.大约在1500年前,我国古代数学典著《孙子算经》中记载了一个历史名题“鸡兔同笼”: 今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何? 这已经渗透了函数的思想.1615年,天文学家、数学家开普勒(Johannes Kepler,1571-1630年)在婚礼上思考酒桶体积算法时,推导出圆的面积计算公式:.17世纪,近代物理学奠基人伽利略(Galileo Galilei,1564-1642年)在研究“抛物线运动的规律”时,证实了以任何角度发射的炮弹,其运动路径都是抛物线[6].

不同时期、不同地域的数学家在“函数的概念”这一主题上做出了许多的贡献,推动函数概念不断演进[7],展现函数概念发展的知识源流与多元文化.

17世纪,德国数学家莱布尼兹(G.W.Leibniz,1646-1716年)提出函数的“幂”定义.1673年,莱布尼茨在其手稿“反切线或函数方法”中创用“functio(英文function)”一词,表示具有特殊作用的某个几何量,如一个图形中的线段.1694年,他在《博学者杂志》中进一步界定“functio”为曲线相关的几何变量,并将其与对应点的横坐标建立关系,由此演变出函数的“幂”定义[7].

18世纪初,瑞士数学家约翰·伯努利(J.Bernoulli Ⅰ,1667-1748年)界定函数的“代数式”定义: 一个变量的函数是由该变量和一些常量,以任何方式组成的量[7].

18世纪中叶至19世纪30年代,教科书普遍采用瑞士数学家欧拉(L.Euler,1707-1783年)给出的“解析式”定义的函数概念: 一个变量的函数是由该变量和一些数或常量以任何方式组成的解析式[7].因“解析式”的函数概念更加易于理解,故广泛受到人们的喜爱.

18世纪40年代后,欧拉进一步更新函数概念的界定,改进为“变量依赖关系”定义,逐渐为人们所接受.1755年,欧拉在《微分基础》更新了函数的定义: 如果某些量依赖于另一些量,当后面这些量变化时,前面这些变量也随之变化,则前面的量称为后面的量的函数[7].

19世纪中叶前,德国数学家狄利克雷(L.Dirichlet,1805-1859年)修正了的函数概念,给出“变量对应关系”定义(1837年),其被公认为经典的“函数现代定义”,简要表述为: 在某区间上,对于每一个确定的值x,都有唯一确定的值y与其对应,使得当x在区间变化时,y也逐渐变化,则称y是该区间上x的一个连续函数.同时,在整个区间上,y不一定按照同一规律依赖于x,也不一定考虑用数学运算来表示两者的关系[7].

20世纪,法国布尔巴基学派提出“集合对应关系”的新定义.综合对1718-1855年45 本西方数学文献、21世纪至今国内现行三版初中教科书的梳理与分析[6],有如下重要的发现.

(1)19世纪中叶前,函数概念的定义基本上以欧拉的“解析式”定义、“变量依赖关系”定义为范本,其主要有两段变化趋势: 19世纪30年代前,欧拉的“解析式”函数概念定义独领群芳; 19世纪40年代后,欧拉改进的“变量依赖关系”的函数定义逐渐受到追捧,呈现后来居上的趋势[7].

(2)国内现行的三版初中教科书中,沪教版教科书与欧拉的“变量依赖关系”定义相近;人教版、北师大版教科书与狄利克雷的“变量对应关系”定义相似,且没有强调该函数为“连续函数”.

在“函数概念”演变历程中,“函数(function)”一词的中文译名蕴含着一段中西方数学家合作交流的奇妙故事,至今在中小学数学教材中仍保留着这一译名.可见,古今中外数学文化是互融互通的.

我国清代数学家李善兰与英国传教士伟烈亚力(A.Wylie,1815-1887年)在翻译《代数学》(1859年)时指出:“凡式中含天,为天之函数”.他们在合译《代微积拾级》(1859年)时写道:“凡此变数中函彼变数,则此为彼之函数”.这两部著作均将“function”翻译为“函数”,因“函”与“含”同义,因此“函数”意思是“含有变数的表达式”,这与函数的“解析式”定义相近[7].

3 教学实践

初中“函数的概念”课例主要围绕“创设情境—讲解新知—交流讨论—课堂小结”的主线展开教学.

3.1 创设情境

创设“滴滴打车”计费、“嫦娥一号”飞行等问题情境,引出教学主题,通过分析多个实例,讲解常量、变量等新知内容.

师: 同学们,在日常生活中使用过“滴滴打车”软件吗?

生: 使用过,外出打车的时候会用到.

师: 假如汽车以一定速度行驶,现以我们学校为出发地,通过软件任意输入上海某一目的地(教师借助希沃投影,展示“滴滴打车”软件,输入东方明珠塔、上海虹桥车站、浦东机场等地址),大家仔细观察,你能发现什么?

生: 目的地不同,打车的车费也发生了变化.

师: 很好! 出发地不变,目的地不同.当汽车速度一定时,随着出发地与目的地之间的距离发生变化,行驶的时间、车费也在发生变化.此时,在速度、两地之间的距离、行驶的时间、车费等量中,哪些量不变,哪些量在变化呢?

生: 速度不变,距离、时间、车费都在变化.

师:“嫦娥一号”是我国首颗绕月飞行的人造卫星.当“嫦娥一号”奔向月球时,在指定轨道飞行的过程中,这个行程与时间(如200 千米、51000 千米、16 小时、48 小时等)会变化吗?

生: 不会变化.

师: 在“嫦娥一号”奔月时,从离开地面那一刻起,时间t和嫦娥一号离地球的距离S会变化吗?

生: 发生变化.

师: 在研究过程中,保持数值不变的量叫做“常量”,可以取不同数值的量叫做“变量”.

3.2 讲解新知

通过“上海市数字教材”平台,借助“插入”、“流转笔记”等功能推送函数的相关数学史料,创设数史情境,帮助学生感知函数,逐步抽象函数的概念.

师: 早在古希腊时期,毕达哥拉斯学派就学会用石子进行计算或推演.例如一个石子用数字1 来表示,两个石子用数字2 来表示,三个石子用数字3 来表示,现在有很多石子,如何表示呢?

生: 用字母n来表示.

师: 这个n是常量还是变量?

生: 变量.

师: 石子的数量与数字之间是否存在确定的关系?

生: 存在确定的关系.

师: 在一场古代战争中,几个部队的士兵不断地聚集前往战场,指挥官想知道有多少士兵参战,于是他要求每位到达的士兵留下一个石子,这样他就可以通过计算石子的数量,得到参战士兵的数量.在这个过程中,士兵的数量与石子的数量是否存在确定的关系?

生: 士兵的数量依赖于石子的数量来确定,他们之间存在确定的关系.

师: 很好! 假设石子数量为x个,士兵数量为y名,能否表示出这种确定的依赖关系?

生:y=x.

师: 17世纪,物理学家在研究地球上抛射物体的路线、射程和所能达到的高度时,发现了如下规律: 炮弹距离地面的高度h(单位: 米)随时间t(单位: 秒)变化的规律为:在这个运动过程中,常量、变量分别是什么?

师:(几何画板演示炮弹运动形成的抛物线,见图2)时间t的取值范围是什么?

生: 0 ≤t≤6.

师: 炮弹距离地面的高度h与时间t之间是否存在确定的依赖关系? 如果存在,怎么表示?

图1

师: 上述问题,都是在一个变化过程中,它们都有哪些共同的特点?

生1: 有两个变量x与y.

生2: 在x特定范围内,y随着x的变化而变化.

生3:y与x之间存在着确定的依赖关系.

师: 很好! 这就是今天要学习的主要内容——函数的概念.在某个变化过程中有两个变量,设为x和y,如果在变量x的允许取值范围内,变量y随着x的变化而变化,它们之间存在确定的依赖关系,那么变量y叫做变量x的函数,x叫做自变量.

3.3 交流讨论

播放微视频,介绍函数概念的演变发展史(见图2),阐述莱布尼茨、约翰·伯努利、欧拉、狄利克雷等数学家对函数概念的定义、“函数(function)”中文翻译的由来,品味数学文化之魅.通过趣味漫画、小组讨论等形式,引发学生对函数概念本质的思考;同时基于常值函数,引导学生从欧拉的“变量依赖关系”的定义过渡到狄利克雷的“变量对应关系”定义,为高中数学学习做好铺垫.此过程中,师生借助“数字教材”平台,通过“流转笔记”等方式进行实时分享,促进跨组之间的交流讨论.

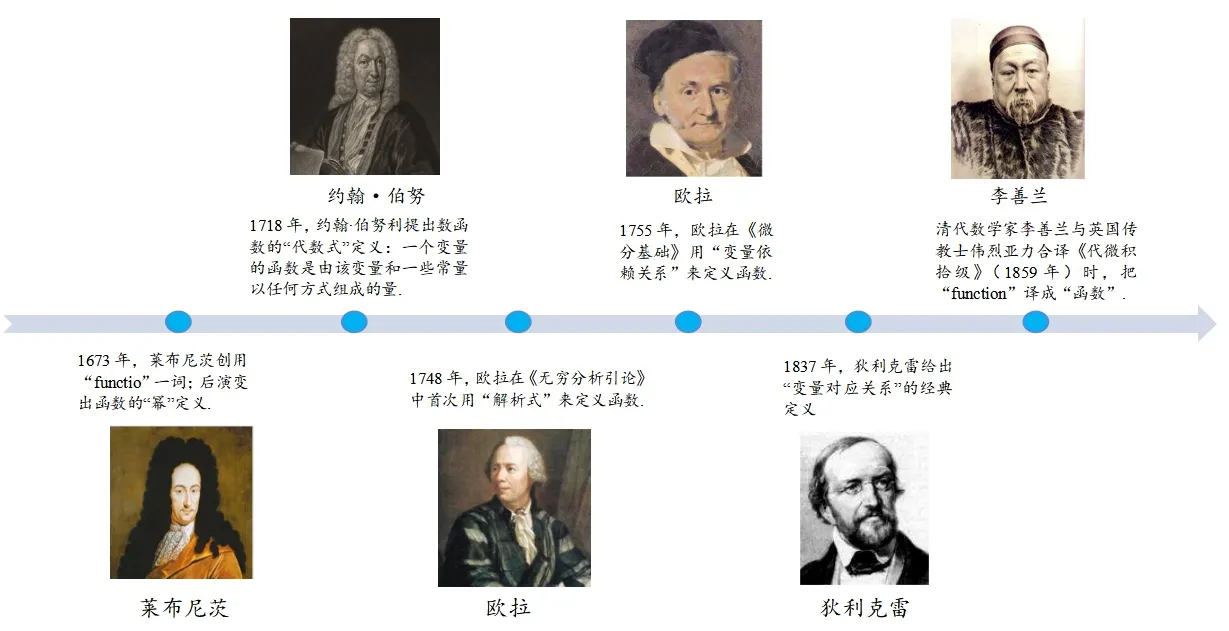
图2

师: 通过微视频,你有什么发现?

生1: 函数概念的演变经历了漫长曲折的发展历程,不同的数学家对函数概念的界定也不一样.

生2: 原来“函数”是“含有变数的表达式”的意思,是数学家李善兰与伟烈亚力翻译时的一种说法.当时,他们采用的是函数的“解析式”定义.

师: 你最喜欢哪位数学家对函数概念的定义? 为什么?

生3: 我最喜欢数学家欧拉的“解析式”函数概念,如y=x等.

生4: 我赞成欧拉“变量依赖关系”的函数定义,因为他提到了两个变量之间存在的依赖关系,容易理解.

生5: 我印象最深刻的是狄利克雷的“变量对应关系”定义,他指明了两个变量之间的对应关系.

师: 接下来,通过这幅“函数机器(function machine)”的趣味漫画(见图3),你又能发现什么?(教师借助平板,实时推送学习材料)

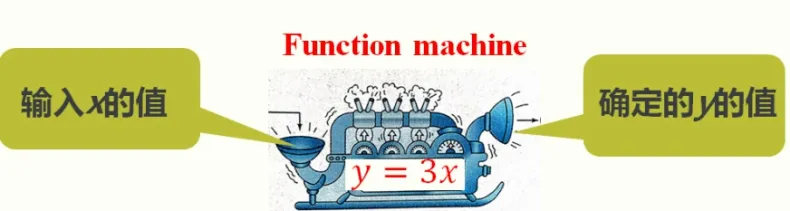
图3

生: 是一个函数,通过输入一个x值,就能得到唯一确定的y值.

师: 很好! 那么y=0 是不是函数?

生6: 不是函数,没有两个变量.

师: 如果把y=0 看作y=0x是不是函数?

生7: 不是函数,两个变量没有确定的依赖关系.

生8: 在欧拉的定义下,y=0 不是函数.但在狄利克雷的定义下,y=0 就是函数.

师: 很好! 在不同的定义下,y=0 是否为函数,均有不同的理解.进一步来看,狄利克雷的“变量对应关系”定义比欧拉的“变量依赖关系”函数定义更加完善,比如常值函数y=0、y=1.

3.4 课堂小结

师: 通过本节课的学习,你有什么收获?

生1: 我学习到了什么是常量、什么是变量,也学习到了函数的概念,它刻画了两个变量之间存在的确定关系.

生2: 函数可以通过解析式法、列表法和图像法三种方式来表达.

生3: 这节课,我了解到在生活、数学史发展中都有函数的影子,数学与我们的生活息息相关.

生4: 通过微视频、趣味漫画,我们交流讨论了欧拉、狄利克雷等数学家对函数概念做出的重要贡献,原来函数概念不是一成不变的,还学习到李善兰与伟烈亚力对“函数(function)”的中文翻译.

4 学生反馈

在“函数的概念”课例教学前、后,对学生的学习情况进行问卷调查与深度访谈.

4.1 教学前

通过问卷前测与访谈,了解到大部分学生对函数概念的了解停留在“解析式”定义上,初步认识到“函数是刻画某个变化过程中两个变量之间的关系”,且对函数概念演变的数学文化知之甚少.

4.2 教学后

通过本节课的学习,几乎全部学生能理解且辨析常量、变量的概念异同.

许多学生对不同数学家界定的“函数概念”有不同的喜好与理解:大部分学生喜欢函数的“变量依赖关系”定义,认为其能够较好地刻画出两个变量之间的变化情况;仅有7.9%的学生支持函数的“变量对应说”,理解常值函数中的变量关系,认为“变量对应关系”的函数定义更加完善、全面.

超过一半的学生表示印象最深的是“函数概念的发展史”的微视频、对不同数学家函数概念界定的交流讨论.

许多学生表示“会通过列举生活例子、数学史例子来讲述两个变量之间的关系,数学与生活息息相关”、“会讲述函数概念的演变历史与数学家界定函数概念的故事”,还有学生谈到“函数”名称的来源,发现古今、中外的数学是相互联系的,表示“原来数学是生动有趣的”.

可见,通过课例教学,学生不仅突破函数学习的认知障碍,加深对函数概念本质的理解,而且对函数的知识源流、社会角色等有更加深刻的认识,对函数发展的多元文化更加感兴趣.这有效地回答了学习函数概念的必要性,为培育学生数学抽象、逻辑推理、数学建模等数学核心素养做好铺垫.

5 结语

实践表明,“函数的概念”课例教学展现数学文化内涵,体现数学史的重要教育价值,彰显信息技术辅助课例教学与评价的有效性、便捷性.

5.1 扎根数史素材,展现数学文化

初中“函数的概念”课例教学扎根数史素材,展现知识源流、社会角色、审美娱乐、多元文化等维度的数学文化内涵,具体如下:

(1)知识源流.借鉴数学史例,展现早期人类对函数的初步感知,帮助辨析常量与变量; 通过历史时间轴,展现函数概念从“幂”定义——“代数式”定义——欧拉的“解析式”定义——欧拉的“变量依赖关系”定义——狄利克雷的“变量对应关系”定义的不断演变,同时介绍我国清代数学家李善兰与英国传教士伟烈亚力对“函数(function)”中文翻译的缘由,追本溯源,展现函数概念发展的知识源流.

(2)社会角色.创设“石子计数”、“鸡兔同笼”和“炮弹轨迹”等历史情境,共同探寻函数的概念及其刻画的变量关系,引导学生感悟“数学来源于生活,应用于生活”的社会角色.

(3)审美娱乐.函数的概念凝结着数学家的智慧结晶,其通过“解析式法”、“图象法”、“列表法”三种方式来表达函数,展现数学的简洁美、统一美;以趣味漫画版“函数机器”来帮助学生理解函数概念,提升数学学习兴趣.

(4)多元文化.不同时空的数学家在“函数的概念”这一主题上做出各自独特的贡献,通过古今对照,中外比较,展现了函数概念演进过程中的丰富人文活动,揭示多元数学文化的相互交融.

5.2 交汇两座桥梁,渗透教育价值

本节课沟通了历史与现实、数学与人文两座桥梁,体现了数学史知识之谐、探究之乐、能力之助、文化之魅、德育之效的重要价值.

(1)知识之谐.本节课基于学生的基本学情,有效地将函数概念的数史文化融入教学中,引导学生以批评性思维来交流讨论,了解欧拉、狄利克雷等数学家在不同时期的函数定义,厘清函数概念不断演进、完善的数学本质,理解函数是刻画变化过程中两个变量之间的确定关系,体现知识之谐.

(2)探究之乐.借助数史情境,引导学生以“概念建构者”的身份,经历不同时代人们对函数的感知与建构的过程,逐渐抽象出函数的概念;接着通过微视频,了解函数概念发展过程中的代表性经典定义,交流讨论函数概念的本质异同,且通过辨析常值函数,体会“变量对应关系”的函数定义是“变量依赖关系”定义的又一次“质的飞跃”.

(3)能力之助.通过生活情境、历史情况,锻炼学生发现问题、分析问题的能力,学会运用函数的眼光来观察、用函数的思维来思考、用函数的语言来表达,为后续培育学生数学抽象、逻辑推理、数学建模等数学学科核心素养做好铺垫.

(4)文化之魅.本节课追寻数学家们的火热思考,展现函数概念建构过程中的数学本质,如欧拉对函数概念的两次修正、李善兰与伟烈亚力对“函数”一词的合作翻译,还原函数概念演进过程中的人文情怀,彰显出数学的文化价值.

(5)德育之效.以“滴滴打车”计费、“嫦娥一号”飞行等生活情境、“鸡兔同笼”、“石子计数”等历史情境,感悟我国科技的蓬勃进步、古人智慧的传承发展.其次,函数概念演变史彰显了数学“以文化人”的教育价值,有效地引导学生“穿越时空,与数学家对话”,帮助学生亲近数学、探究数学、理解数学,了解不同时空下数学家的独特贡献,形成动态的数学观.回顾李善兰对“函数(function)”中文翻译的贡献,增强文化自信.

5.3 融入信息技术,助力教学评价

本节课借助上海市教研室研发的“数字教材”平台,将相关史料插入“数字教材”,借助“插入”、“云笔记”等功能辅助教学,有利于推送每节课相关知识的数学史料、微视频等学习资料,帮助学生了解函数概念的相关历史,理解函数概念的演变动因.同时,借助“反馈练习”、“流转笔记”等功能,在课前、课后及时测评,在课中保障师生交流互动、实时共享.可见,融入信息技术的数学文化课例教学,大大推动了数学“教—学—评”的系统化,助力数学学科“立德树人”的教育实证.