新课程标准视角下新教材第九章“统计”的新变化

广东省佛山市顺德区罗定邦中学 李定平 汤旭红 越勇

现在,各地开始用新教材[1]教学,在教学中逐渐体会到新教材比旧教材[2]更加注重知识的内在逻辑联系,更加重视数学思想方法的产生发展过程,必修第二册第九章“统计”的变化更是很大(见表1),一些概念也发生了一些根本性的变化.然而,不得不说,受惯性思维的影响,就连一些期末统考试题都还停留在旧的认知中.

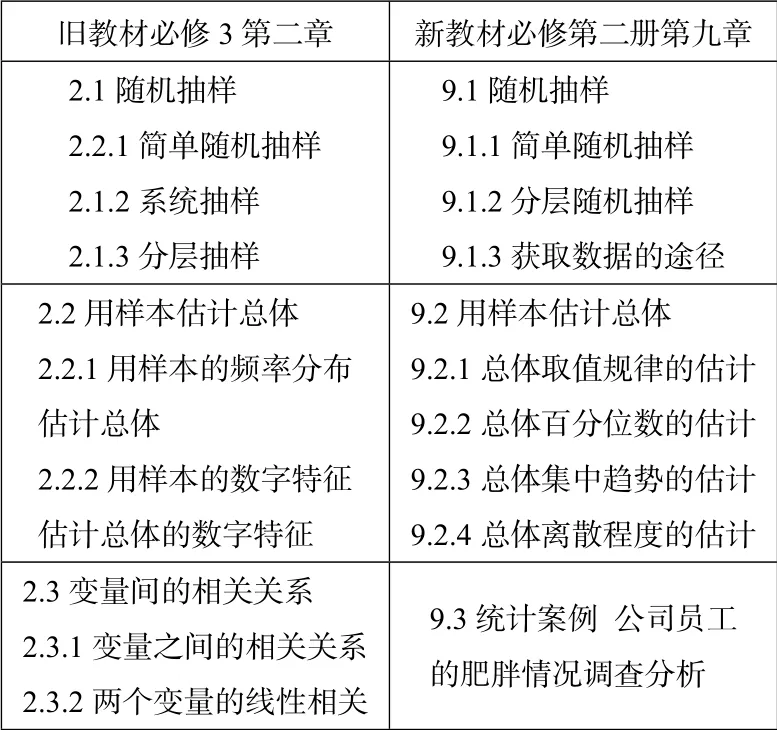
表1 新旧教材目录对比

章建跃博士说“理解数学是教好数学的前提”,作为一线教师就是先要理解教材,课本承载着课程标准,体现国家意志.也只有理解了课本,才能设计出符合出学生认知规律、把握教学内容及其蕴含着数学思想方法、符合数学知识发生发展过程的自然脉络问题,然后学生再根据教师设计的问题的引导下独立自主地开展观察、分析、综合、比较,知识得以自主建构,素养得以自然发展.本文就是根据在使用新教材教学过程中遇到的困惑,通过对新、旧教材进行对比分析所作的思考.

1 增加了相关概念的严谨性定义

开始学习统计时,会对统计的相关概念进行熟悉与了解,常常会遇到以下困惑老师与学生的问题:

题: 为了了解全校240 名学生的身高情况,抽取40 名学生进行测量,下列说法正确的是( )

A.总体是240 名学生

B.个体是每名学生

C.样本是40 名学生

D.样本容量是40

原教材没有明确给出总体、个体的概念,我们均认为研究对象的全体是总体,每一个研究对象是个体,而研究对象是学生的身高,所以答案是 D.

然而进行了新教材的教学后,我们发现新教材对总体、个体进行了非常清晰明确的定义——在一个调查中,我们把调查对象的全体称为总体,组成总体的每一个调查对象称为个体.为了强调调查目的,也可以把调查对象的某些指标的全体作为总体,每一个调查对象的相应指标作为个体.也就是说研究学生的身高情况时,我们可以将某地所有高中生作为总体,每一个高中生作为个体,也可以将某地所有高中生的身高数据作为总体,每一个高中生的身高数据作为个体,因为根据新教材中的定义知道,身高值可以作为调查对象的一个指标值.此题答案就所有选项均可.

2 抽样方法顺应了时代发展

2.1 删除了系统抽样

原教材是这样说“从上所说可知,简单随机抽样有操作简便易行的优点,在总体个数不多的情况下,是行之有效的.但是,如果总体中的个数很多时,对个体编号的工作量太大.即使使用随机数法操作也并不方便快捷.另外,要想“搅拌均匀”也非常困难,这就容易导致样本的代表性差.因此,为了操作上方便快捷,在不降低样本的代表性的前提下,可以采取下面的抽样方法——系统抽样”.

现在除小剪刀锤子布、彩票中奖号由10 个小球的产生,在生活中比较少用抽签法了,取而代之是的电脑派位、电脑摇号,当然也就无需“搅拌均匀”了,由于新技术的出现,操作也简便,人们的意识也逐渐适应了电脑随机抽签,总体中个体数再多都可以用产生随机数的办法进行,而且不需要去剔除不能整除的余数,更方便高效更好理解.根本不再需要做小纸条签了,当然没有“搅拌均匀”困难,适应时代发展删除系统抽样就自然而然了.

2.2 突出了分层的本质

原教材是这样说“一般地,在抽样时,将总体分成互不交叉的层,然后按照一定的比例,从各层独立地球取一定数量的个体,将各层取出的个体合在一起作为样本,这种抽样方法是一种分层抽样”.

新教材如此说“一般地,按一个或多个变量把总体划分成若干个子总体,每个个体属于且仅属于一个子总体,在每个子总体中独立地进行简单随机抽样,再把所有总体中抽取的样本合在一起作为总样本.这样的抽样方法称为分层随机抽样,每一个子总体称为层,在分层随机球样中,如果每层的样本量都与层的大小成比例,那么称这种样本量的分配方式为比例分配”.

分层抽样的本质目的之一是为了防止出现“极端样本”;之二是可以重点研究某些“层”——“在每个子总体中独立地进行简单随机抽样”,这样一来就有下面变化:

新教材中的“分层抽样”不一定按层的大小成比例分配每层的样本量,个别层可以适当多抽样本,当然也可以按每层的样本量都与层的大小按比例分配分配样本量,这就是按比例分配样本量的分层抽样.所以说很多地区还在照搬原来的考查分层抽样的题目的不严谨之处在于没有明确分层抽样是否“按比例分配样本量”,如果不按比例分配样本量,则答案是不确定的.

课本第184 页练习第3 题也例说了各层按比例分配样本和不按比例分配样本的分层抽样.

“在每个子总体中独立地进行简单随机抽样”,由于新技术的应用,可以随意突显某层样本的均值与方差,自然就需要计算出总样本的均值与方差(如课本第216 页第11 题),由于不再是确定的按比例分配样本量的分层抽样,在求总样本的均值时,学生容易错误地将各层样本均值的均值当作总样本的均值.

3 更加突显了统计思想

有人说统计没有对错,只有好坏.统计就是获取数据和分析数据,新教材在抽样后面增加了一节9.1.3 获取数据的途径,让学生知道获取数据的基本途径,除了普查和抽样还有统计报表和年鉴、社会调查、试验设计、互联网等.

在开展“统计”的9.1.1 节的教学时,教材安排的是两个课时——第一课时是简单随机抽样的介绍,第二课时则对总体和样本均值的分析,让学生理解样本均值的统计有或然性,感受统计思维与确定性思维的差异.这也是较旧教材的一个很大的改进.特别是在课本第178-179 页的探究中,对样本量为50 和100 的样本各选取10 个进行观察,分析样本平均数的均值与总体均值的关系并用图形表示,可以让学生体会到样本的随机性,不同的样本的均值是不同的,样本均值也具有随机性,是与总体均值是一个确定的数是不同的.更进一步,虽然样本均值与总体均值不同,我们会发现样本均值都是在总体均值附近波动.而在实际教学中,很多老师都是忽略这一课的.我们还可以注意到整个第九章在使用各个统计量解决问题时,都非常严谨地区分总体的和样本的,比如在介绍方差概念时就给学生介绍了总体方差和样本方差的概念,并强调了我们常常是用样本方差去估计总体方差,而样本方差依赖样本选取,具有随机性.殊不知这一节中对于提高学生对统计思想的认识是很有必要的,让学生理解样本估计总体思想,体会选取有代表性的样本的重要性,知道在条件允许的情况下增加样本量的作用.

4 增加了统计图的选择

“一幅图胜过一千个文字”,用统计图将统计后数据之间的关系用视觉化的图形表示,直观形象便于读取,一目了然.

新教材删除了茎叶图(茎叶图并不是统计图,而是数据的呈现方式),增加了一个典型案例“已知某市2015年全年空气质量等级如表和2016年5月和6月的空气质量指数数据,选择合适的统计图描述数据,并回答下列问题……”,既然要选择,那就需要让学生对各种统计图作系统理解,为此教材作了全面说明:

扇形图主要用于直观描述各类数据占总数的比例,条形图和直方图主要用于直观描述不同类别或分组数据的频数和频率,折线图主要用于描述数据随时间的变化趋势.条形图适用于描述离散型数据,直方图适用于描述连续型数据等.

5 呈现了提取数字特征的过程和拓广了统计特征的刻画方法

新教材在从数的角度分析数据时,在原来的两个角度-——集中趋势与离散趋势的基础上,增加了百分位数.高中系统学习的特征数只有两个,就是百分位数与方差,虽然方差初中已涉及,百分位数也是在中位数的基础上来开展学习的.且新教材对这两个特征数概念的呈现方式也完全一样,也符合一般观念下的数学概念学习方式.

首先是通过问题引入为什么要建立百分位数:

“问题2: 如果该市政府希望是80%的居民用户生活用水费支出不受影响,根据9.2.1 节中100 户居民用户的月均用水量数据,你能给市政府提出明确居民用户月均用水量标准的建议吗?

其次如何建立百分位数:

“把100 个样本数据按从小到大排序,得到第80 个和第81 个数据分别为13.6 和13.8,可以发现,区间(13.6,13.8)内的任意一个数,都能把样本数据分成符合要求的两部分,一般地,我们取这两个数的平均数并称此数为这组数据的第80 百分位数,或80%分位数”.

再次将概念求法一般化并给出严格定义:

“一般地,一组数据的第p百分位数是这样一个字,……”

最后再通过两个例题(离散数据与掩盖真实数据的频率分布直方图)巩固说明百分位数的求法.

新教材如此编写让我们清晰地理解了:

p%分位数(中位数)的应用意义——为决策服务;统计特征——是数据的一种划分、是分界数; 具体求法——中位数求法的一般化.

上述80%分位数的提取过程也展示了统计特征的刻画方法,使学生经历较为系统的数据处理全过程,在此过程中学习数据分析的方法,理解数据分析的思路,运用所学知识和方法解决实际问题,自然地发展了数据分析核心素养.

6 增加了统计变换,提高了数学运算要求

新旧教材都有要求会根据具体数据求平均数、中位数、方差等,根据掩盖了原始数据的频率分布直方图来估计样本的平均数、方差等.这都体现了在统计这一章节去提升学生处理数据的能力以及数学运算能力.

而新教材“有时为了计算方差的方便,我们还把方差写成以下形式读作:“方差=样本数据平方的均值-均值的平方”,这样引入了方差公式的一个变式,自然就有方差定义与变式之间的互化:

另外课本第212 例6 还用了很大的篇幅来介绍根据样本各层的平均数和方差来求总样本的平均数和方差.笔者认为这不仅与前面的分层抽样方法相呼应,同时也是一个基本运算技能,也为后面学习线性回归分析做了铺垫.既然给出两种方差定义式,已知各层的平均数和方差来求总样本的方差也有两种方法:

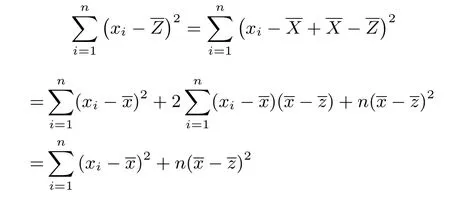
我们又可以得到另一个分层抽样的总样本方差的化简式子.课后习题还让给推广了总体划分为3 层的分层抽样的总样本平均数、方差的求解,学生也可以类比去推导(课本第216 页第11 题).

方差定义与变式的互化、已知各层样本均值与方差求总样本方差的两种方法,这些运算变换是在统计中专门出现的,我们称之为统计变换,是培养学生运算能力的素材,其运算过程让学生感觉的难点是带求和符号,可先通过3 个样本数据的运算扩大到带求和符号的运算,以降低难度.带求和符号的运算对运算想象与运算素养是很有裨益的.

可见“统计”这一章的新旧教材变化确实是很大的,也只有理解了这种变化才能使我们的教学适应这种变化.在教学实践的过程中要善于发现问题,除了自己思考外,还要与同事之间讨论,在讨论中碰出思维的火花,才能让我们的理解更深刻,特别对于已形成思维惯性的老教师尤其如此.时代在发展,历史在进步,新老教师都要努力学习才能与时俱进.

附1:(课本第184 页练习第3 题)高二年级有男性490人,女性是510 人,张华按男生、女生进行分层,通过分层随机抽样的方法,得到男生、女生的平均身高为170.2cm 和160.8cm.

(1)如果张华在各层按比例分配样本,总样品量为100,那么在男生、女生中分别抽取了多少名? 在这种情况下,请估计高二年级全体学生的平均身高.

(2)如果张华从男生、女生中抽取的样本量分别为30 和70,那么在这种情况下,如何估计高二年级全体学生的平均身高更合理?