初中数学建模课程的探究与实践思考*——以商品的价格规律问题为例

北京市十一学校龙樾实验中学(100096)彭芳芳

中国科学院院士李大潜提到“数学建模是数学与工业、数学与创新的最佳结合点”.从当前各国数学课程改革来看,通过数学建模建立数学与外部世界的联系成为共同关注点.如美国课程标准将主要内涵为“认识到并能应用数学于数学之外的情境中”的“数学联系”作为重要目标.《义务教育数学课程标准(2011年版)》指出,“模型思想的建立是学生体会和理解数学与外部世界联系的基本途径”[1].

数学建模是一个从发现问题、分析问题、解决问题到解释、应用、推广、预测、评价的学习全过程,在渗透模型思想的同时,有助于培养学生的应用意识、创新意识,提高综合实践能力.

1 课程现状与可行性分析

近年来,基于社会和课程标准对数学建模核心思想的强调,不少高中开设了数学建模课程,以北京的高中为例,如北京师范大学附属中学的“课内延伸,内外结合”模式,首都师范大学附属中学的“课外活动”模式,北京市第十五中学的“调查报告式”、“论文研读式”,北京市十一学校的“大学先修”模式等.

初中数学建模课程的开展与实践还在探索阶段,初中开设数学建模课程面临的困难主要集中在两个方面: 一是数学工具和方法不够,学生在初中阶段学习到的数学知识和数学工具有限,不具备深度开展数学建模的条件;二是社会支持不够,初中阶段学生开展数学建模课程没有直接的培养出口,导致学校、教师、学生和家长不愿意投入时间和精力开展此项课程.

初中阶段的数学建模课程是否具有可行性? 通过广泛调研,笔者认为是可以的.首先,初中阶段的学生已经具备从现实生活或具体情境中抽象出数学问题的抽象能力;第二,初中阶段的学生已经具备基本的解释现实问题的数学思想和工具,比如利用数学符号建立方程、不等式、函数等模型工具表示数量关系与变化规律;第三,可以通过积极有效的对比实验、专家讲座等多种方式展示数学建模课程的价值,赢得学生、家长等社会相关群体的认可.

2 数学建模的基本过程

以“同种商品不同型号的价格规律问题”为例,笔者从问题背景、模型假设、模型建立、模型的评价与优化、模型的应用、模型的推广等维度谈谈对数学建模的基本过程的思考与实践.

2.1 课题背景

数学与外部世界的联系,是数学发展到今天其在自身的舞台上最精彩的表演[2].美国课程标准中强调,各种水平的数学学习,应包括有机会解决在数学以外的情境中产生的问题,既可与其他学科建立联系,又可与学生的日常生活相联系.《义务教育数学课程标准(2011年版)》在总目标中也明确提出,“体会数学知识之间、数学与其他学科之间、数学与生活之间的联系”[1].因此,在选择课题时,应以生产生活实践、跨学科为背景,特别是学生身边正在发生的事例,或正在学习的跨学科知识为背景,丰富背景的趣味性和多样性,让学生感受数学应用的广泛性,体会数学研究的价值,激发数学学习的兴趣.

下面是“同种商品不同型号的价格规律问题”的问题背景: 在超市中经常看到这样的情况,同种商品有大小不同的型号,比如A 牙膏有50 克、90 克、135 克等规格,对应的价格分别3.1 元、5.1 元、6.8 元.那么同种商品不同型号的价格有没有什么规律呢? 你能否预测规格为210 克的该品牌牙膏的价格?

2.2 模型假设

现实背景的问题大多是非良构问题,在教学过程中,可根据不同年龄阶段学生的学习基础、认知能力以及个别化差异,引导学生进行适当的模型假设,将非良构问题转化为结构性知识.

在“同种商品不同型号的价格规律问题”中,对于八年级的学生,可以假设: 牙膏的价格与对应规格呈线性关系.

2.3 模型建立

在课堂模型建立环节,要给学生留有主动建立模型的时间与空间,启发式教学,以问题串的形式,引导学生逐步抽象问题、分析问题、建立模型、解决问题,积极参与学习过程.

回到“同种商品不同型号的价格规律问题”中,引导学生以表格的方式整理问题背景中的信息,如表1所示.

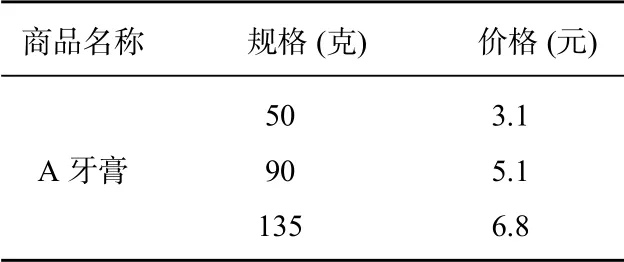
表1 A牙膏不同型号信息表

问题1: 这些价格是如何制定出来的? 其中有什么规律?

问题2: 如果A 牙膏生产出一种新的型号,应该定价多少?

问题3: 我们在选择商品规格时,如何从价格上判断哪种更合算?

【模型建立】设牙膏的规格为x克,对应价格为y元,根据模型假设,牙膏价格与牙膏规格呈一次函数关系,于是建立模型y=kx+b.任意选择牙膏的两组数据,根据待定系数法确定系数k,b,可得如表2所示的线性模型,其图象如图1所示.

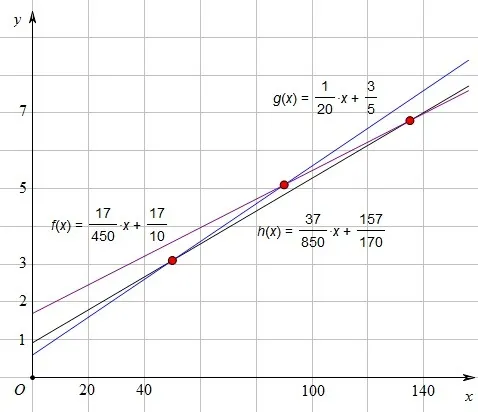
图1

表2 A牙膏的三种线性模型

2.4 模型的评价与优化

如前文所述,实际问题通常比较复杂,为了建模过程的可操作性,需要作一些必要的假设,这可能会导致模型的解与实际情况产生偏差,因此我们需要对模型进行评价和优化.模型的评价与优化需要借助数学工具,多角度地分析、对比、评价,是一个综合考量的过程,有助于发展学生的高阶思维,培养创新能力.

回到“同种商品不同型号的价格规律问题”中,从图1 中可以发现,对于每一条拟合直线,都恰有一个实际点不在该直线上,也就是说,各个模型与实际情况均出现偏差,这是由于模型关系中的线性假设造成的,那么这三条拟合直线,到底哪条的拟合程度更好呢?

为了更真实的反映数据之间的关系,需要尽可能地提高直线的拟合程度.直线的拟合程度由实际值与拟合函数值的偏差决定,偏差越小,拟合程度越高,因此我们可以通过实际值与拟合函数值的偏差来评价拟合程度.对于初中阶段的学生,可以引导其从绝对差、差的完全平方、相对差等角度进行分析评价,并对比发现不同评价法对评价结果的影响.

绝对值评价法: 绝对值评价法根据实际值与拟合函数值的差的绝对值来描述偏差,绝对值评价法认为,在线性拟合的函数中,将各点的函数值与实际值的差的绝对值相加,所得和越小,拟合程度越高.

完全平方评价法: 完全平方评价法根据实际值与拟合函数值的差的平方来描述偏差,完全平方评价法认为,在线性拟合的函数中,将各点的函数值与实际值的差的平方相加,所得和越小,拟合程度越高.

考虑到同样是1 元的偏差,对于价格为10 元的商品与价格为100 元的商品,意义是不同的,当绝对误差不能真实反映线性拟合的优劣程度时,可以考虑相对误差评价法.

相对值评价法: 相对值评价法根据实际值与拟合函数值的差的绝对值与实际值的比值来描述偏差,相对值评价法认为,在线性拟合的函数中,将各点的函数值与实际值的差的绝对值与实际值的比值相加,所得和越小,拟合程度越高.

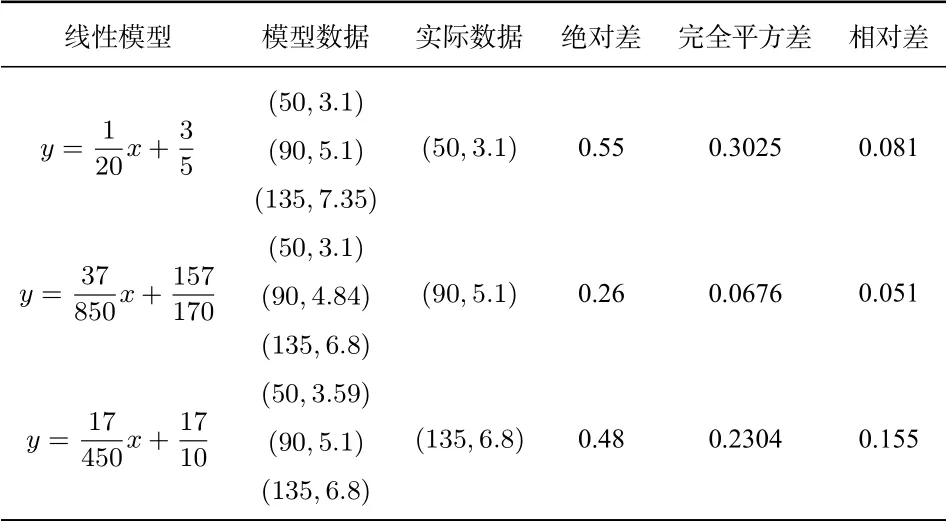
表3 不同评价法对偏差的认识

在教学中,可以引导学生展开以下讨论: ①不同的评价方法对评价结果的影响; ②自主设计评估方法并论证其合理性,应用该评估方法对模型的拟合程度进行分析、评价.

2.5 模型的应用

模型建立后,可以引导学生应用模型预测和解决问题,收获课题成果,体会模型的价值,激发学习内动力.

在“同种商品不同型号的价格规律问题”中,应用模型,可以预测给定规格的A 牙膏的价格,比如预测规格为210g的A 牙膏的价格,如表4所示.

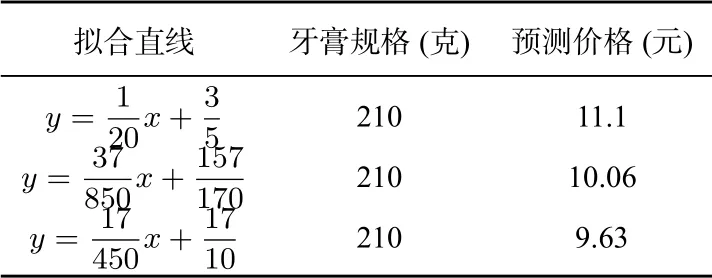
表4 利用拟合直线预测A 牙膏的价格

2.6 模型的推广

模型的推广是从特殊到一般,提炼思想的过程,有助于提高学生的迁移应用能力,培养系统思维和创新意识.

在“同种商品不同型号的价格规律问题”中,课题背景给出了A 牙膏的三种不同型号与对应价格.现实生活中,情况可能会更复杂,对于同一种商品,可能有超过三种不同的型号(如四种,五种甚至十多种),那么同种商品不同型号的价格与规格的关系是否也能进行类似的拟合与评价?

例如,某超市B 品牌的洗发液有50 毫升、200 毫升、400毫升、750 毫升四种规格,对应价格分别为8.5 元、18.5 元、34元、58 元.这些价格是如何制定的? 有什么规律? 如果该品牌的洗发液生产一种新规格,应该如何定价?

3 作业与评价

课程的落地,离不开适切、精准的评价,评价不仅是对学习结果的检验,也是对学习过程的考查.有效地设计、组织和实施评价,不仅可以帮助教师了解学生的学习状况、诊断学习效果、改进教学质量,还可以帮助学生及时有效的认识到自己的学习过程和状态,激发学生的学习兴趣,提高学生学习的信心.

评价的设计主要要关注两个点: 作业的开放性和评价的多元化.开放性作业是多元化评价实施的前提和载体,多元化评价包括多维度的评价内容:“知识与技能”、“过程与方法”、“情感态度价值观”,多样化的评价工具和多元化的评价主体.

还是以“同种商品不同型号的价格规律问题”为例,作业如下.

请你以小组为单位,到附近的超市收集同种商品不同型号的价格,探索其中的价格规律.要求:

1.数据真实有据,附照片为证;

2.建立的模型科学、合理;

3.运用适当的方法评估模型;

4.应用模型解决实际问题;

5.谈谈你的思考.

同时,笔者设计了学习过程自评量表、成果研究报告、成果分享PPT、调查问卷等评价工具.学习过程自评量表基于数学建模各个环节的过程学习而设计,由学生对照各项标准自我评价;成果研究报告,从系统研究、学术规范等角度评价,成果研究报告的书写激励学生及时总结反馈,固化成果,由同伴与教师共同评价;成果分享PPT 的演示,能够实现成果的发布、交流与评价,由同伴与教师共同评价;调查问卷基于自信心、内动力、情感收获等维度设计,由学生自主评价.各项评价工具对应的评价内容、评价主体如表5所示.

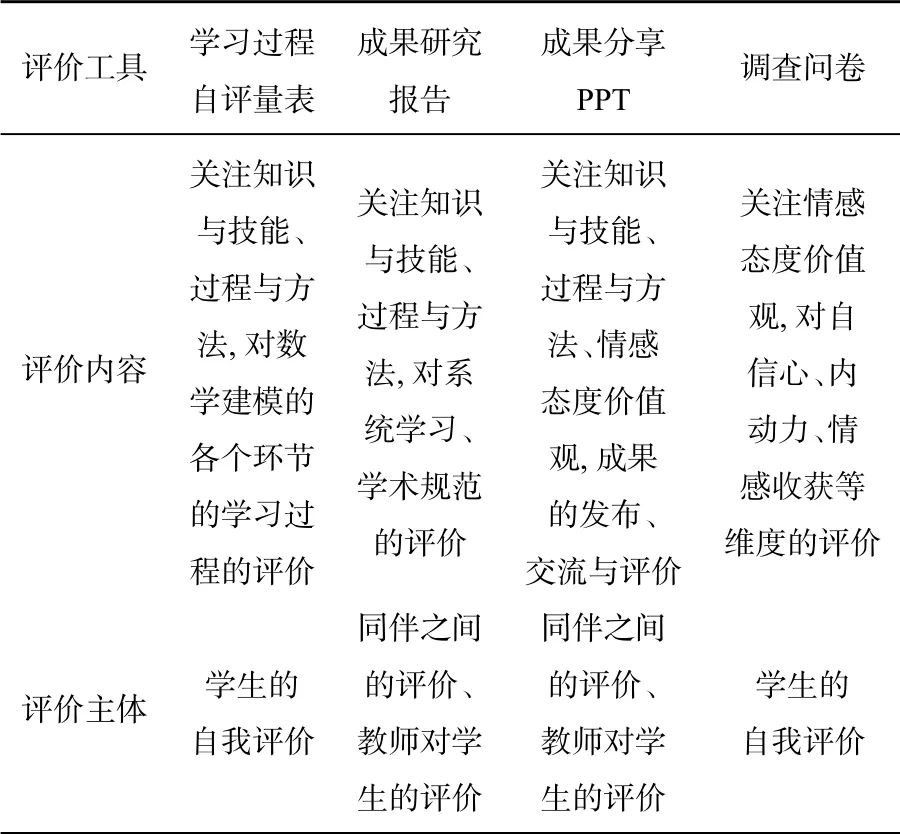
表5 评价工具的多元化评价