基于深度学习的“微专题”教学分析与设计<br/>——以“一次函数与面积问题”为例

基于深度学习的“微专题”教学分析与设计
——以“一次函数与面积问题”为例

2022-04-24广东省佛山市顺德区龙江外国语学校528318白彩云

中学数学研究(广东) 2022年6期

广东省佛山市顺德区龙江外国语学校(528318)白彩云

广东省佛山市顺德区龙江里海学校(528318)陈明炽

1 引言

微专题教学为何会引起教师关注,因为微专题主要针对的是学生在练习中暴露出来的薄弱环节,一般都是学生知识缺失的地方,所以也就更能引起学生的兴趣,激发学生的深度学习.它立足于学情、教情、考情,选择一些切入小、角度新、针对性强的微型专题,力求解决教学中的真问题、小问题和实问题.微专题的“微”,是来自学生学习的难点或疑点,是解析某一种数学问题过程中想不到或不注意的突破口,是容易发生偏差与疏漏的思想方法、思考角度,且这种“突破口”、“思想方法”、“思考角度”在解析其他知识问题或题型时同样会出现,真正的“微”是“突破口”、“方法”、“角度”.微专题的“专”是指解析数学问题或题型过程中影响正确结论的某一点知识、某一种思维方法、某一个思考角度等.这就需要教师立足在“点”、“角度”、“方法”,将相关的各“数学问题”、各类“题型”组织起来,集中“火力”专门解决这类问题“小切口”的教学.

微专题的作用是主要体现在应用变式教学促进深度学习,它整合联系一类问题横向和纵向的深入,引导学生对典型方法进行提炼,深度探究,拓展数学思维.微专题教学的目标指向是: 基础知识、基本技能、基本思想(数形结合、分类讨论),基本数学活动经验.微专题教学的素养指向是: 数学建模、数学运算、数学抽象、逻辑推理、直观想象、数据分析.

微专题提思维,改编教材,分散难点,穿插教学,提分磨尖.微专题虽是“小专题”,却体现“大智慧”.微专题教学应该是什么样的教学? 如何进行微专题教学设计? 本文就“一次函数与面积问题微专题”教学设计案例进行解析探究.

2 研课标

2.1 显性关联的课标: 函数、三角形面积、坐标与图形位置

(1)探索简单实例中的数量关系.(求函数表达式,数学建模和待定系数法)

(2)能确定简单实际问题中函数自变量的取值范围,并会求出函数值.(列、解不等式组,最值,配方法)

(3)能用适当的函数表示法刻画简单实际问题中变量之间的关系.(图像法、解析式法,列表法)

(4)结合对函数关系的分析,能对变量的变化情况进行初步讨论.(变量的取值范围,分类讨论思想)

(5)会写出三角形的顶点坐标,体会可以用坐标刻画一个简单图形.(坐标的意义,直线平行与垂直的直观感知,作辅助线——坐标轴的垂线)

2.2 隐性关联的课标: 方程、不等式、尺规作图、坐标与图形运动

能根据具体问题中的数量关系列出方程,体会方程是刻画现实世界数量关系的有效模型.(函数与方程的思想)

能根据具体问题的实际意义,检验方程的解是否合理.(会做解题后的反思、验证解(多个解时)的合理性)

3 磨考题

3.1 考题集锦

题1(佛山市顺德区2019 学年第一学期期末教学质量检测第22 题)如图,在平面直角坐标系xOy内有一直线对应的一次函数是.

(1)在x轴上画出对应的点A;

(2)若直线l经过点A,求直线l与坐标轴所围的三角形面积.

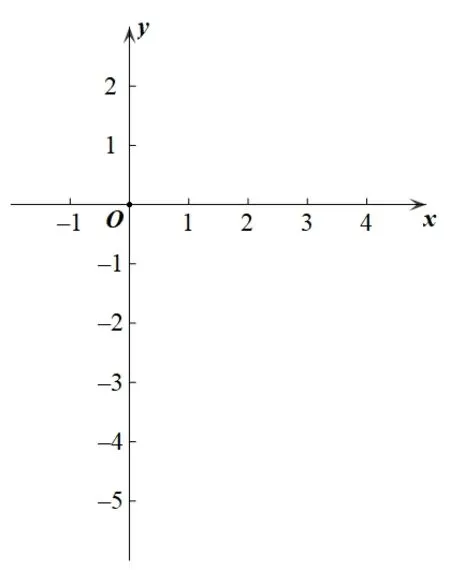
题1 图

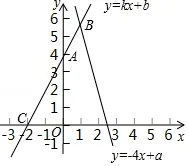
题2 图

题2(佛山市顺德区2018 学年第一学期期末教学质量检测第23 题)已知点A(0,4),C(-2,0)在直线l:y=kx+b上,l和函数y=-4x+a的图像交于点B.

(1)求直线l的表达式;

(2)若点B的横坐标是1,求关于x、y的方程组的解及a的值.

(3)若点A关于x轴的对称点为P,求ΔPBC的面积.

3.2 解题反思

3.2.1 立意解读

(1)考点梳理: 一次函数与平面直角坐标系为情境的综合题,主要考查一次函数的定义(求函数解析式)、一次函数与二元一次方程(组)的关系、利用坐标转化为线段的长度求三角形的面积等知识.

(2)设问方式: 三角形的存在性问题,即由存在三角形求点的坐标,再转化为线段长度.

(3)技能要求: 处理方程和方程组计算的运算能力(先化简后求值的解方程),构造图形面积的几何直观作图(作坐标轴的垂线)、利用割补方法挖掘求三角形面积的数感.

(4)解题思维: 易想难求(解决三角形面积问题的方法容易想得到、如何确定不规则三角形的底和高是思维突破的难点、列出方程后的解方程是运算的难点).

3.2.2 障碍梳理

(1)解方程(组)的运算、复杂方程(无理数系数)的求解.

(2)确定三角形的底和高的方法.

(3)动点问题分类讨论的全面性.

(4)点的坐标与线段的长度的转化.

3.2.3 方法归纳

(1)求一次函数的解析式时用待定系数法.

(2)求点的坐标用解方程(组)法.

(3)作图构造三角形的高辅助数形结合法.

(4)分析动点三角形面积时需要用到对应的思想进行分类讨论法.

(5)探究的思路: 先根据题目条件求出一次函数,再确定所求三角形的底(一般选择落在坐标轴上的线段作为底),然后根据底确定高的情况(一般是解方程得到交点的横坐标或纵坐标作为高).

4 教学设计

(一)教学目标对解决此类问题的几个障碍点形成有效地解决方法,能形成解决一次函数与三角形问题的思维范式和操作程序.

(二)教学关键三角形面积模型的整合与构造、重在关联和生成联系.

(三)教学重点讲审题、讲障碍、讲方法、讲思维、讲联系、讲变化

(四)教学方法问题驱动法、启发讲授法、交流内化法

(五)教学流程

1、障碍点突破讲练

预习稿:

(1)如图 1-1,点A,B,C的坐标分别为(3,2),(1,0),(4,0),则ΔABC的面积为____.

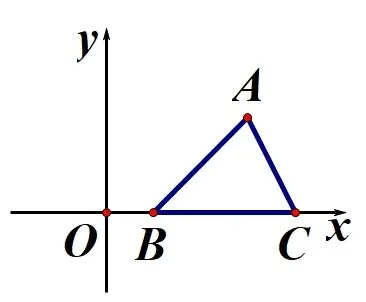
图1-1

(2)如图 1-2,点A,B,C的坐标分别为(-1,3),(-3,0),(2,0),则ΔABC的面积为____.

图1-2

(3)如图1-3,点A,B,C的坐标分别为(-1,3),(-3,-2),(2,-2),则ΔABC的面积为____.

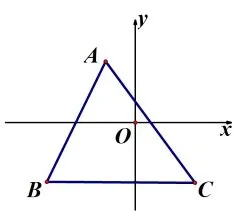
图1-3

(4)如图1-4,已知点A、B的坐标分别为(1,2),(3,0),点C在x轴上,且ΔABC的面积为5,则点C的坐标为____.

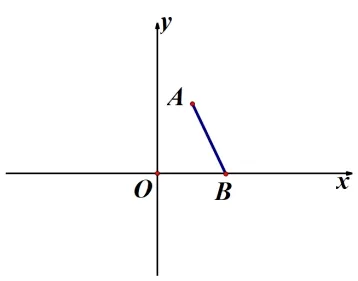
图1-4

(5)点M(3,4)到x轴的距离是____,到y轴的距离是____,到原点的距离是____.

(6)已知点P在坐标轴上,且OP=3,则点P的坐标为____.

(7)已知在平面直角坐标系中有一点P,它到x轴的距离为3,到y轴的距离为5,则点P的坐标为____.

(8)直线y=-x+6 与x轴的交点坐标是____,与y轴的交点坐标是____.

(9)画出直线y=2x+2 与直线y=-x+6 的草图,并求它们的交点坐标.

(10)如图1-5,求直线y=-x+ 6 与坐标轴围成的ΔABC的面积.

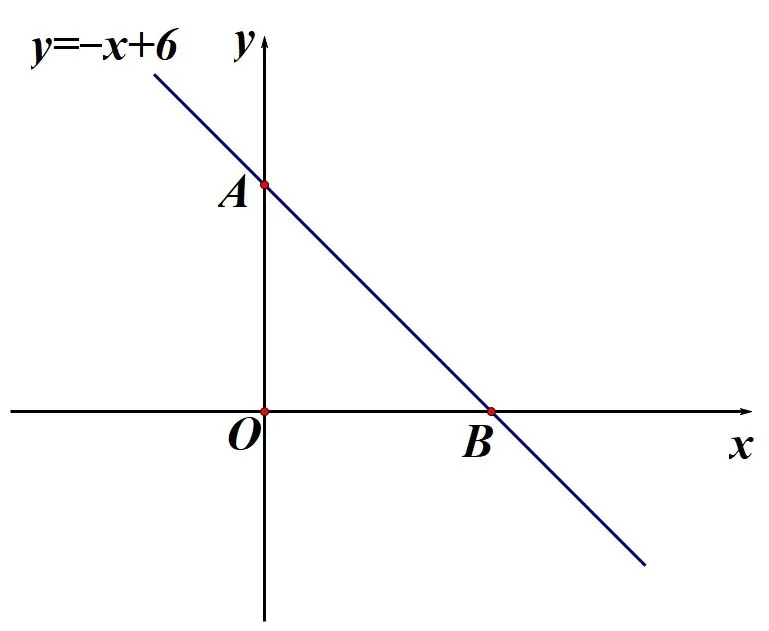
图1-5

设计说明本环节设计目的是解决学生的画图障碍、计算障碍和点坐标转化为线段长的障碍.要求学生课前完成,教师课前5 分钟进行总结求三角形面积的方法以及点评在函数求三角形面积的技巧利用点的坐标转化为底和高.

2、核心问题思维生长

【定点问题】

1.动手探究: 请你在右图上添加一条直线,与原图构成一个封闭图形,并求出这个新图形的面积.要求:(1)添加的直线要标出表达式;(2)交点用大写字母标图;(3)你所选的新图形,要涂上阴影.我添加的直线是____.我提出的问题是: 求____.

我还有另一种方案,添加的直线是____.我提出的问题是: 求____.

设计说明本环节采用让学生构建知识关联,发展学生思维训练,老师通过递进问题驱动学生思考,通过追问引领学生总结与反思,从而让学生自己形成类型1 能直接确定底和高的面积问题解题方法: 交点坐标转化为线段长.

2.如图2-1,在上面的图上,添加直线y=2x+2,与原直线y=-x+6 交于点C,与两坐标轴分别相交于点D,E.求ΔCEB的面积.

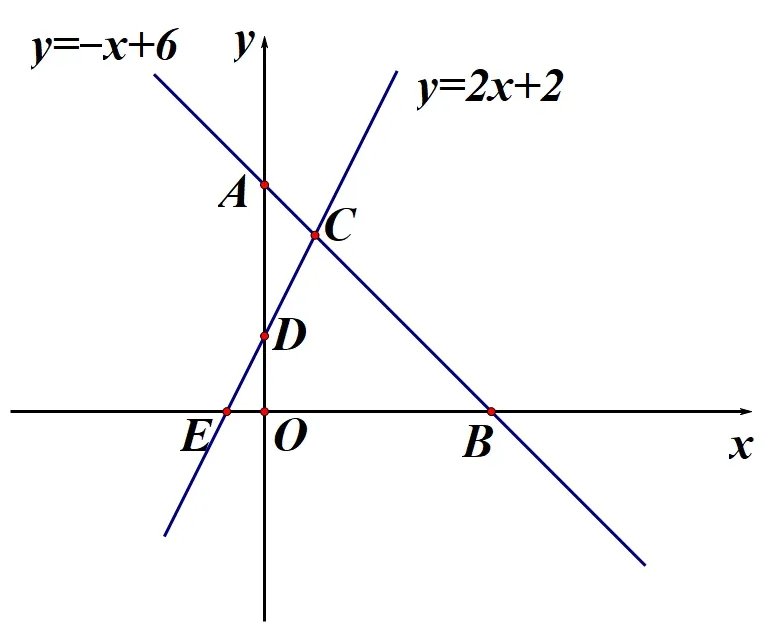
图2-1

设计说明本环节设计这个典型问题能聚焦方法与模型,核心问题驱动,构建知识关联,发展思维训练,形成类型1: 能直接确定底和高的面积问题的解题方法和程序.本环节教师需板书解题过程,并进行解题步骤总结,这是解题规范性的必须,也是“复杂问题简单写”提高解题速度的必须.

变式1 图

3、关联问题思维生长

变式1: 在第2 题的基础上,过点B,再多加一条直线y=-2x+12,与直线DC交于点F,求ΔFCB的面积.

设计说明本环节的变式训练“方法悟于过程,变式指向本质”,聚焦典型问题的变化与拓展,聚焦聚合思维,形成类型2: 不能直接确定底和高的面积问题的解题技能,课堂训练可结束,但深度思考却不停步.

4、解题总结

(1)解题方法总结

(2)解题步骤(程序)总结

①找——交点坐标,②列——方程或方程组,③解——解方程(组),④化——交点坐标转化为线段长度(底和高),⑤求——三角形面积(直接求或割补法).

5、深化拓展

变式2: 阴影部分有何异同?

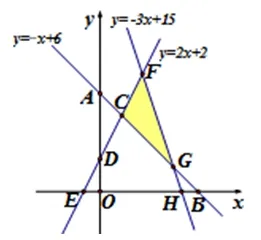
变式3: 如图,动点M在线段OC和射线CA上运动,上否存在点M,使ΔAOM的面积是ΔCOB的? 若存在,求出此时点M的坐标;若不存在,请说明理由.

变式3 图

变式4 图

变式4: 如图,动点P在折线O - C - B上运动,设ΔPOB的面积为S,请用含x的代数式表示S.

设计说明本环节根据给出情境对母题进行改编,做变式教学,由定点的三角形面积问题深化到动点的三角形面积问题,加深对本节课知识的整体理解,围绕三角形面积这个知识点,形成相互关联、思维递进的知识链,让学生从不同角度、不同类型和不同特点出发,在学习训练过程中建构知识体系,考虑如何根据不同类型的实际问题,转化为同类型的图形和数学方法.