高中数学课堂渗透课程思政思想课例分析

范雪敏

摘要：n次方根与分数指数幂这节内容，目标在于掌握根式的性质、根式与分数指数幂间的互化，了解指数幂中指数从整数到有理数的拓展过程，理解有理数指数幂的意义与运算性质.为了在课堂中渗透课程思政的思想，特选取双十一成交额及GDP的指数爆炸型增长、新疆北鲵碳14断代法等实例作为线索，落实立德树人总目标.

关键词：n次方根，分数指数幂，课程思政

一、思政点睛

章前引言通过介绍距今5000多年前就存在的良渚遗址，指出它对研究中华五千年文明的起源具有重要意义，也是弘扬中華文化的宝贝素材.自然地引出考古学家是借助碳14断代法这个指数函数模型来推测其年代的，为学习指数函数提供了实际背景.此外，章前引言还列举了其他背景实例，如细胞分裂、人口增长、放射性物质的衰减等问题，进一步指出本单元需要类比前一单元幂函数的研究方法，研究指数函数与对数函数，这为后面的学习提供了现实背景方向，强调这两种函数模型的现实意义以及重要性，同时渗透数学建模的核心素养.

二、教学构想

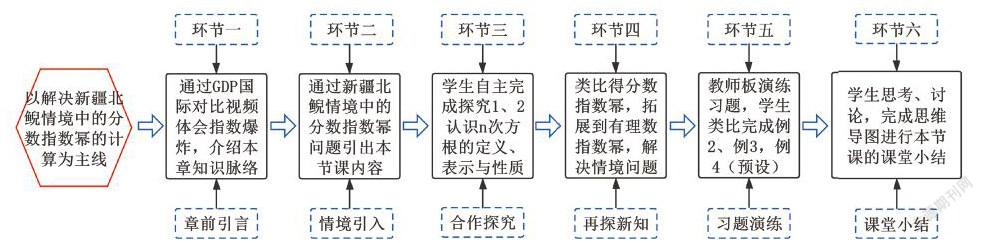
作为本单元的起始课，n次方根与分数指数幂是拓展实数指数幂的基础，具有奠基性作用，更是为研究指数函数做好准备.本课时教学环节设计如下图：

三、教学环节

（一）章前引言

师：双十一余热还在，这个视频反映了历年双十一成交金额的变化情况，请大家直观感受购买力变化！（播放视频）每年双十一成交金额都会远超前一年，呈指数爆炸型增长，这日益强大的购买力背后，是我们稳步走向全面小康的底气！小到我们的购买力，大到国家的GDP，近几十年的变化都反映了中国在以指数爆炸般不断壮大！

这里的指数爆炸其实是本章所要学习的指数函数模型，本章我们将类比幂函数的研究方法，深入研究指数函数和对数函数，学会根据实际情况选择合适的函数类型构建数学模型，从而反映现实问题.

◆思政点睛：

从身边正在发生的问题（双十一）出发，借助视频直观感受指数爆炸增长，引出指数函数模型，为介绍本章知识脉络做铺垫，反映数学在现实生活中的重要作用;引导学生关注强大购买力背后的真相——中国日益强大，全面进入小康社会，培养学生的爱国情怀和国家认同感、自豪感.

（二）情境引入

学生观看新疆北鲵图片，猜是什么动物.

师：它叫做新疆北鲵，它的祖先生活在2亿5千万年前，和恐龙一起生活过，但后面随着地壳的运动，大部分新疆北鲵灭绝了，还有一小部分极幸运地活下来了，可以说是活化石了！它们目前就生活在博乐温泉县，大家有机会可以去温泉县北鲵基地看看！你知道考古学家是怎么判断出来它生活在2亿5千万年前的呢？

生：碳14法.

师：碳14断代法，人们发现生物体内的碳14含量P，会随着死亡时间t的变化而变化，得到了这个关系式.它说明，当死亡时间为5730年，碳14含量P= ，当死亡时间为6001年，碳14含量P= ，当指数幂中的指数从整数变成分数时，这个式子的意义和运算性质究竟是什么？带着这些问题，我们一起走进今天的内容.

◆思政点睛：

通过我们新疆本地的“活化石”北鲵，一方面引出考古学家是怎样断定新疆北鲵生活的年份问题，从而介绍碳14断代法，自然地引出分数指数幂的意义和运算问题，引出本节课的主题;另一方面向学生科普我们身边的“活化石”，培养学生保护濒危动物的决心，以及对故乡的认同感和自豪感.

◆设计意图：

n次方根的第一个性质比较简单，可以直接通过其意义得到，故直接由学生口答即可，但第2个性质对于学生来说稍微复杂些，涉及到分类讨论思想，故交给学生小组探究完成;借助探究2中的众多例子，将难度降低，由浅及深，帮助学生从具体到一般归纳性质.

通过例1巩固n次方根的概念与性质，教材中没有第4问，但从第3题直接跨度到第5题对学生来说稍难，故设置了第4题进行过渡，由易到难，将难点拆解.

（四）再探新知

问题3：根据n次方根的定义和数的运算（a>0）： ， ，这是被开方数的指数能被根指数整除时的情况，当不能整除时，根式是否也可以表示为分数指数幂的形式（a，b，c>0）？试完成下列式子的化简：

师：我们希望整数指数幂的运算性质，如（ak）n=akn，对分数指数幂仍然适用.因此作出规定，正数的正分数指数幂的意义是 .

◆设计意图：

通过被开方数的指数能被根指数整除的情况实例，类比给出不能被整除的情况，并自然地给出正数的正分数指数幂意义的规定，由于教材上略去了规定合理性的说明，考虑到学生的实际学情，此处不展开探究;此外小练习是以讲练结合的形式，帮助学生从特殊到一般，再从一般到特殊进一步理解结论.

追问1：类比负整数指数幂的意义，正数的负分数指数幂的意义是什么？

教师引导学生类比初中学过的负整数指数幂的意义，不难得到正数的负分数指数幂的意义 ，讲练结合，学生口答负分数指数幂化根式的练习

追问2：类比0的整数指数幂的意义，0的正分数指数幂和负分数指数幂的意义是什么？

教师引导学生类比初中学过的0的整数指数幂的意义，不难得到0的正分数指数幂是0，0的负分数指数幂没有意义.教师引导学生发现，规定了分数指数幂的意义以后，幂ax中指数x的取值范围就从整数拓展到了有理数.

解决刚才的问题：考古学家正是利用了有理数指数幂的知识，计算出生物死亡6001年后体内碳14含量P的值为 即生物死亡6001年后体内碳14含量P约为原来的48.4%.

◆思政点睛：

类比初中学过的负整数指数幂的意义、0的整数指数幂的意义，学生能够得出正数的负分数指数幂的意义以及0的正分数、负分数指数幂的意义，引导学生体会类比思想在数学学习中的重要性.

学生在得到结论后仍难以发现幂中指数已从整数拓展到有理数，这里教师要加强引导，让学生感受到指数范围的扩充，体会到数学知识间的联系性和整体性.再前后呼应回到之前的问题，解决了碳14断代法中分数指数幂的意义和计算问题，能够帮助学生加深对分数指数幂的理解，并体会到数学的实际应用意义.

（五）习题演练

◆设计意图：

将整数指数幂的运算性质拓展到有理数指数幂后，有理数指数幂的功能就更加强大了，此处的练习旨在帮助学生体会运算性质的综合应用，同时能够引导学生将底数换成合适的幂形式，简化问题，为学生独立完成例2、例3做铺垫.

（六）课堂小结

小结：回顾这节课，你有什么收获呢？请以小组为单位，从知识和思想方法的角度展开讨论，完成思维导图.

结语：数学史上最早将指数的范围从整数扩充至有理数的，是数学家John Wallis，有了这个基础，我们才能在下节课将指数的范围继续扩充到实数，这样就给我们将来研究指数函数奠定了坚实的基础！

希望大家这两节课打好基础，将来去研究生活中更多的指数爆炸模型，来感受中国各个方面的飞速发展！

◆思政点睛：

为更好地帮助引导学生梳理本节知识脉络，以思维导图的方式让学生小组合作完成，帮助学生养成梳理知识点的学习方法.

通过结语部分：为了亲自感受到中国方方面面的高速发展，我们要打好指数运算的基础，以此再次激发起学生认真学习指数这一节的兴趣，这其中渗透学科育人环节，在课堂中贯彻落实立德树人的根本任务.

参考文献：

[1]汪晓勤，邹佳晨.高中数学教学中实施课程思政的路径[J].数学教学，2021（08）：1-6.