基于转矩估计与磁链补偿的SRM转矩脉动控制*
2022-03-04党选举
党选举,张 超
(桂林电子科技大学电子工程与自动化学院,桂林 541004)
0 引言
近年来,开关磁阻电机(switched reluctance motor,SRM)因具有结构简单、制造成本低、系统可靠性高及调速范围广等特点,成为新能源汽车、航天航空等领域驱动装置的首选[1]。由于SRM双凸极结构、磁路高度饱和、磁滞效应和强非线性等原因,导致建立精确数学模型较为困难,从而造成SRM 在低速运行中产生较大的转矩脉动,严重制约了SRM的发展与应用[2-4]。因此,针对SRM转矩脉动抑制控制策略的研究,具有重要理论与工程价值。
在SRM传统的控制中,电流斩波控制是将电流作为被控量对SRM进行控制,虽然控制简单但并不能达到理想的效果。王勉华等[5]对比了CCC控制和DTFC控制策略,DTFC对转矩脉动抑制具有更好的效果。CHEOK等[6]将转矩和磁链作为被控量对SRM进行控制,但磁链模型是利用磁链特性表对磁链进行查询,会造成较大的误差。并且实际过程中转矩并不可测,在SRM驱动应用中,精确的电磁转矩模型对于SRM转矩控制至关重要,利用力矩传感器会带来较高的成本。为了构建准确的转矩模型,ZHANG等[7]改进了高斯函数拟合方法,利用转矩观测器进行转矩估计,通过拟合5个固定位置磁链表达式推导了电磁转矩模型。此方法虽然得到了电磁转矩,但是只考虑到5个特殊位置,局部误差较大不可避免。EVANGELINE等[8]通过二维有限元方法利用LSSVM设计SRM转矩参数回归模型,实现对转矩脉动进行抑制。但因为未知量过多,计算较为复杂,也很难推广到工程应用中。李孟秋等[9]利用BP神经网络构建了SRM的转矩观测器,但并未充分考虑到SRM的转矩特性,网络结构较为复杂。
本文根据SRM的机理特性设计了神经网络对转矩进行估计,解决转矩获取问题,将转矩脉动引入到磁链控制中,对磁链实时补偿,获得准确磁链信息,在磁链滞环的配合下对SRM转矩脉动进行抑制控制。
1 SRM数学模型
SRM内部电磁特性极其复杂,忽略磁路饱和影响以及磁通边缘效应,SRM电磁转矩表达式为:
(1)
系统磁共能为:
(2)
将式(2)带入式(1),可得系统转矩-电流模型为:
(3)
式中,L为绕组电感;i为绕组电流;T为电磁转矩;W′为系统磁共能;θ为转子位置角;ψ为绕组磁链。
由文献[10]可知,SRM实际转矩可表示为:
(4)
由式(4)可知,SRM输出转矩和磁链相关,可以通过控制磁链对SRM的转矩脉动进行抑制控制进行控制。
2 传统SRM磁链控制
基于TSF传统磁链控制系统[11]如图1所示,转速 PI调节根据转速偏差输出转矩控制量Tref,利用转矩分配函数根据转子位置角θ将转矩控制量合理地分配到各相,通过转矩逆模型将相转矩Tk转换为相参考电流ψk,利用滞环比较器对磁链进行控制,实现SRM转矩控制。

图1 传统SRM磁链控制系统
SRM换相时转矩应该满足下式:
(5)
式中,Tk为第K相参考转矩;fk(θ)为第K相转矩分配函数。GAN等[12]对比分析了常用的4种TSF:立方型、指数型、线性型、余弦型,其中立方型TSF具有更好的性能,其表达式如下:
(6)
式中,θon为转矩增大时开通角;θoff为转矩减小时关断角;θov为换相重叠角。
3 基于转矩估计SRM磁链补偿控制
基于TSF传统磁链控制,并没有考虑将转矩脉动信息反馈到控制过程中,导致转矩脉动过大。本文通过构建转矩估计器将瞬时转矩引入到控制系统中,在磁链模型基础上,利用转矩偏差经过PD控制器对磁链进行实时补偿,从而得到更为准确的磁链信息,在磁链滞环配合下对SRM进行控制。基于转矩估计和磁链补偿的SRM转矩脉动抑制控制如图2所示。

图2 基于转矩估计和磁链补偿的SRM转矩脉动抑制控制
3.1 SRM转矩估计器设计
实际运行过程中,SRM的转矩模型并不可知,根据式(3)可利用神经网络构建SRM的转矩-电流模型,根据SRM的机理特性设计了激活函数和预处理解析表达式,神经网络拓扑结构如图3所示。

图3 SRM转矩特性神经网络结构
网络结构输入层为X=[i,θ,F(i,θ)],预处理函数F(i,θ),隐含层激励函数为fj=[f1,f2,…,fn],隐含层权值向量为wj=[w1,w2,…,wn],网络输出为T=wTh+ε。
3.1.1 神经网络输入预处理函数的设计
本文采用电磁转矩预处理函数为:
(7)
式中,Lq为定子凸极和转子凹槽中心对应饱和电感;Ldast为定转子凸极中心完全对齐位置的电感;A、B为拟合系数;f(θ)为位置角函数。A、B、f(θ)表达式分别为:
A=ψm-LdastIm
(8)
(9)
(10)
式中,Nr为转子极数;Ld为定子凸极与转子凹槽中对应的饱和电感;ψm为最大磁链值;Im为最大磁链下的电流值。
考虑SRM的转矩特性具有较强的非线性特性,因此引入LE等[13]提出的转矩非线性解析表达式作为神经网络的预处理函数,通过对输入样本数据预处理优化了神经网络,使得在固定网络结构下提高精度和训练速度。
3.1.2 神经网络激励函数的设计
党选举等[14]根据输入信号的先验知识设计隐含层元激励函数,与Sigmoid函数、径向基函数等通用激励函数相比,能够简化网络结构并提升网络性能,更有效率的解决问题。受该文启发,本文根据SRM转矩基本变化规律设计神经网络隐含层激励函数为:
(11)
式中,I′是由电流进过CSF电流分配得到的值用来调节函数形状;bj代表隐含层的基宽向量值;k决定函数凹陷宽度;cj代表隐含层的中心坐标向量值,c与当前的导通相有关,当参数选取得当即可使得激活函数曲线近似于SRM转矩特性。本文取b=0.2,k=0.05,根据SRM三相周期性导通规则,该文令c遵守以下约束。
(12)
式中,c的取值应该在当前导通相θon与θoff之间,使激励函数类似于SRM的电磁转矩特性,取值范围较宽,该文c1=[10,0]T,c2=[40,1]T,c3=[70,0]T,隐含层激励函数的设计目的是为了能够更好的描述SRM的转矩特性。SRM的转矩特性和激励函数图形如图4所示。
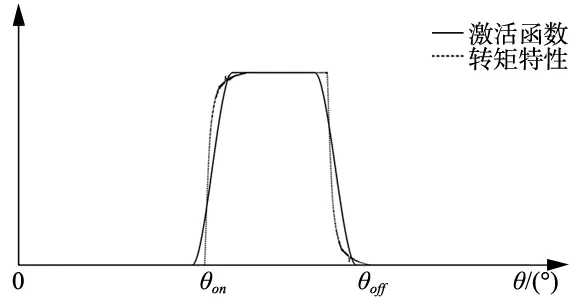
图4 SRM的转矩特性和激励函数图形如图
由图得知,激励函数形状和SRM的转矩特性类似,所设计的激励函数可以表达SRM转矩的基本变化趋势。
3.1.3 神经网络训练过程
神经网络通过误差反向传播算法进行在线学习训练。选取性能指标函数为:
(13)
式中,ut是网络逼近误差;Te是神经网络实际输出;Tref是参考转矩。通过训练使ut趋近于0,进而使得输出转矩Te能更好地跟踪参考转矩Tref。转矩模型中Te更接近Tref,系统的动态性能就更好。
自适应学习率就是让学习率的大小适应网络的训练。当损失函数曲面较为平缓时,加大学习速率,损失函数曲面振荡较为剧烈时,减小学习速率,提升网络收敛性。
假设L(k)、L(k-1)分别是批次k和k-1批次的损失函数,β(k)为损失函数的变化率[15]。
(14)
则k+1批次的学习率δ(k+1)为:
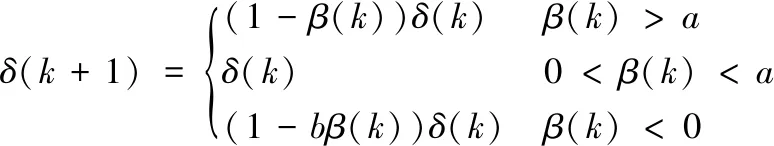
(15)
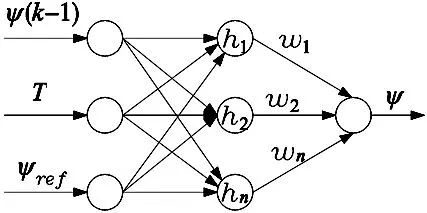
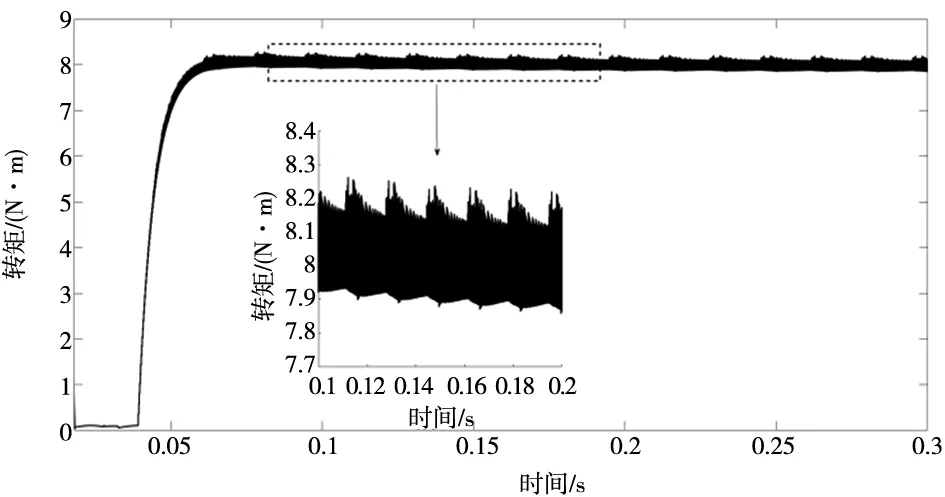
式中,阈值0 学习过程中按照误差负梯度方向调整[16]。具体训练步骤如下: 步骤1:随机初始化网络参数,为简单计算,这里将神经网络初始权值wj的初始值设为随机值,学习速率η初始值设为0.5。性能指标ε为0.000 1。 步骤2:根据当前参数值计算神经网络输出值,代入式(15)。计算经过n-1次调整后性能指标函数为E(k),若E(k)≤ε则算法结束,否则跳至步骤3。 步骤3:根据梯度法调节神经网络中参数公式如下: (16) 式中,α∈(0,1)为动量因子,其中取α=0.4。a=0.25,b=0.05,且a值的越大,学习速率调节越快。 步骤4:设n=n+1,返回步骤2。 本文该神经网络使用的是3-5-1的结构,该网络结构隐含层激励函数根据SRM的转矩特性设计,并且加入可以初步反应非线性的解析表达式作为网络的预处理函数,充分利用了SRM的机理特性,使得神经网络可以在减少节点的条件下增强神经网络的泛化能力和系统的鲁棒性。 传统的电压模型中定子磁链是通过直流脉冲法获取得到[17]。为了获得准确的磁链模型,本文通过动态RBF映射转矩磁链关系,并利用转矩模型得到的磁链偏差,对磁链进行前馈补偿,从而得到更为准确的磁链信息。 RBF神经网络描述非线性映射时采用多层前向网络,但是这种网络不能反映系统的动态特性,因此,为了能够正确估计出定子磁链,使RBF神经网络具有良好的动态特性,采用将输出反馈到输入的动态神经网络结构。基于动态RBF神经网络磁链辨识拓扑结构如图5所示。 图5 动态RBF神经网络结构 网络结构输入层为X=[ψ(k-1),T,ψref]T,隐含层激励函数为hj=[h1,h2,…,hn],隐含层权值向量为wj=[w1,w2,…,wn]T,网络输出为ψ=wjThj,隐含层激励函数为高斯函数为: (17) 则误差性能指标为: (18) 转矩偏差Δt经过PD控制器处理输出uf作为神经网络的误差信号进行在线自学习。在控制初期或出现较大误差时,由通过转矩估计的反馈控制,系统能够保持稳定。在磁链模型通过一段时间自学习后得到SRM的转矩-磁链模型,系统由反馈控制过渡到磁链模型的控制。 采用梯度下降法,则RBF神经网络调整算法为: (19) 式中,η∈(0,1)为学习速率;α∈(0,1)为动量因子。 本文采用的神经网络结构为3输入1输出的三层网络结构,根据文献[18]可得隐含层神经元个数计算式为: (20) 式中,n,m分别为输入层和输出层神经元个数;a为1~10内的整数。由此计算和实验验证可得隐含层个数为8,最终确定3-8-1的网络结构。 通过动态RBF神经网络可得转矩-磁链逆模型,控制系统单相磁链为ψk,为了能够得到准确的磁链信息,通过PD控制求得磁链补偿量,对磁链进行补偿。 若采样时间足够小,系统在某一个角度处于平衡,可近似认为∂ψ/∂θ≌Δψ/Δθ,则转矩变化量为[19]: Δt=iΔψ/Δθ (21) 采样时间非常小时,可认为采样时间内i保持不变,令kp=i·Δθ,则有: Δt=kpΔψ (22) 根据上式通过常规PD控制器可将转矩偏差转化成磁链偏差转化成磁链补偿量。补偿后得磁链则为: (23) 补偿后的磁链近似于SRM实际输出磁链,通过磁链滞环比较器对SRM进行实时控制。 为验证该文所提出控制策略的有效性,在MATLAB/Simulink中搭建三相6-4极SRM控制系统仿真模型,主要仿真参数设置如表1所示。 表1 SRM主要参数 利用转矩脉动系数衡量转矩脉动大小,定义如下[20]: (24) 式中,Kt为稳态时SRM转矩脉动系数;Tmax为稳态时最大瞬时转矩;Tmin为稳态时最小瞬时转矩;Tav为稳态时平均转矩。 在MATLAB/Simulink的控制仿真中设SRM给定负载转矩为Tt=8 N·m恒定不变,给定转速wref=300 r/min,分别对基于TSF的传统磁链控制仿真、基于RBF动态神经网络的磁链控制的仿真和基于转矩特性神经网络瞬时转矩估计的SRM磁链补偿与控制仿真。 基于TSF的传统磁链控制如图6所示,其中图6a~图6c分别表示SRM相磁链、相电流以及相转矩波形;图7为SRM输出总转矩波形,其中包含波形的局部放大。当系统进入稳定状态,对应转矩脉动系数为4.50%。 图6 基于TSF的传统磁链控制相磁链、相电流及相转矩波形 图7 基于TSF的传统磁链控制输出总转矩波形 基于RBF动态神经网络的磁链控制仿真结果如图8所示,其中图8a~图8c分别表示SRM相磁链、相电流以及相转矩波形;如图9所示为SRM输出总转矩波形,其中包含波形的局部放大。当系统进入稳定状态,对应转矩脉动系数为1.98%。 图8 基于RBF动态神经网络的磁链控制系统相磁链、相电流及相转矩波形 图9 基于RBF动态神经网络的磁链控制系统总转矩波形 基于瞬时转矩估计与磁链非线性补偿控制仿真结果如图10所示,其中图10a~图10c分别表示SRM相磁链、相电流以及相转矩波形;图11为SRM输出总转矩波形,其中包含波形的局部放大。当系统进入稳定状态,对应转矩脉动系数为1.22%。 图10 基于瞬时转矩估计的SRM磁链补偿与控制系统相磁链、相电流及相转矩波形 图11 基于瞬时转矩估计的SRM磁链补偿与控制系统输出总转矩波形 以上三种控制策略仿真结果如表2所示,其中包括最大转矩Tmax、最小转矩Tmin、平均转矩Tav以及转矩脉动系数Kt。 表2 三种控制策略对比 在给定负载8 N·m进行采样,为简化模型复杂度,仅取单相的位置、电流和转矩的数值,通过神经网络训练得到估计转矩值和实际转矩值对比如图12所示。 图12 转矩神经网络瞬时转矩估计和实际参考转矩对比 本文通过得到参考转矩利用动态RBF神经网络得到的估计磁链和补偿后磁链和参考磁链对比分别如图13~图14所示。 图13 估计磁链和参考磁链对比 图14 补偿后磁链和参考磁链对比 如图12所示,基于SRM转矩特性设计的转矩估计器可以很好跟踪实际运行时的参考转矩,如图13和图14所示,利用动态RBF神经网络构建的转矩磁链逆模型可以得到较为准确的磁链模型,通过磁链补偿后可以得到理想的磁链信息。 设定系统在0.2 s时负载由8 N·m降至5 N·m,基于传统BP神经网络转矩估计控制和基于转矩特性神经网络转矩估计控制变负载仿真如图15所示。 图15 传统BP神经网络和转矩特性神经网络变负载控制 由上面仿真结果可知,基于TSF的传统SRM磁链控制,由于并没有考虑到转矩脉动因素,导致转矩脉动过大,不利于SRM恒转矩控制;基于RBF动态神经网控制,构建了较为准确的转矩磁链逆模型,对转矩脉动的控制具有一定的抑制作用;基于SRM转矩特性瞬时转矩估计和磁链辨识控制通过进一步利用SRM 的转矩模型,实现对控制过程中的磁链非线性前馈补偿,改善了系统动态品质,减小系统转矩脉动。同时,在变负载控制过程中,由于转矩特性神经网络转矩估计控制策略更能体现出SRM的机理特性,相较于传统BP神经网络能够对负载变化做出更快反应,使整个控制系统具有良好的动态响应特性。 本文充分考虑到SRM强非线性特性,设计了两种神经网络分别对转矩和磁链进行了估计。根据SRM的转矩特性,设计了神经网络的激励函数和输入预处理函数,建立了较为精确的转矩模型。在构建的磁链模型基础上,利用转矩估计器求得磁链偏差对磁链进行实时补偿,获得理想的磁链信息,从而通过磁链控制抑制SRM的转矩脉动。通过仿真对比表明,相较于传统控制方案,该控制方案在降低控制系统复杂度的同时,能更好抑制转矩脉动和更强的抗干扰能力,对于SRM研究具有一定意义。3.2 基于动态RBF神经网络磁链估计

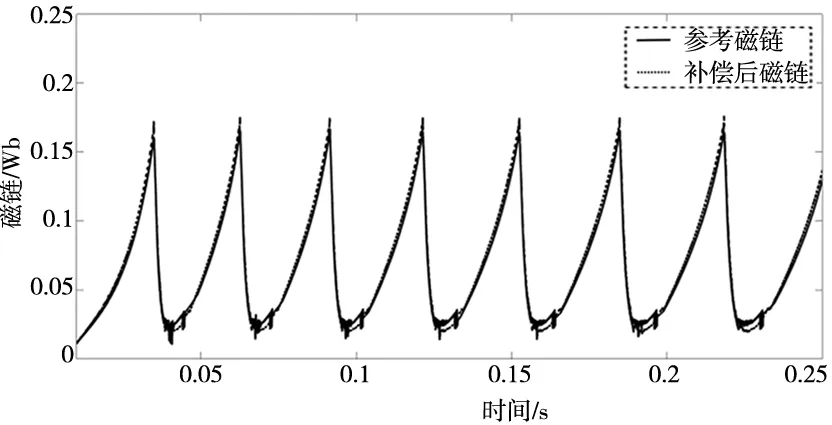
3.3 估计磁链的实时补偿
4 仿真验证

4.1 恒定负载仿真


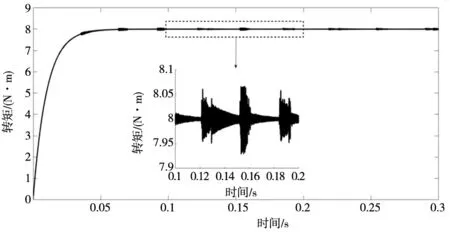
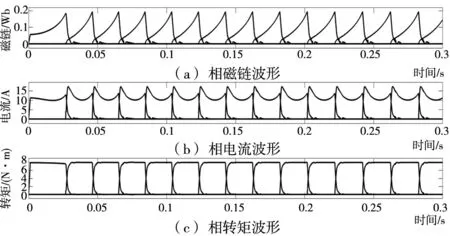

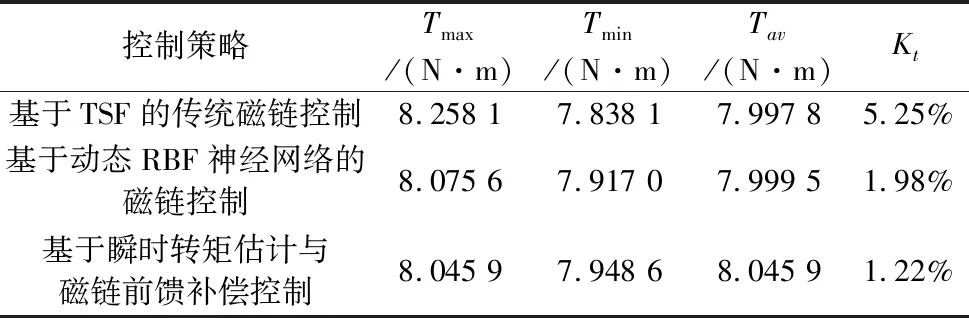
4.2 SRM转矩估计和磁链补偿仿真对比
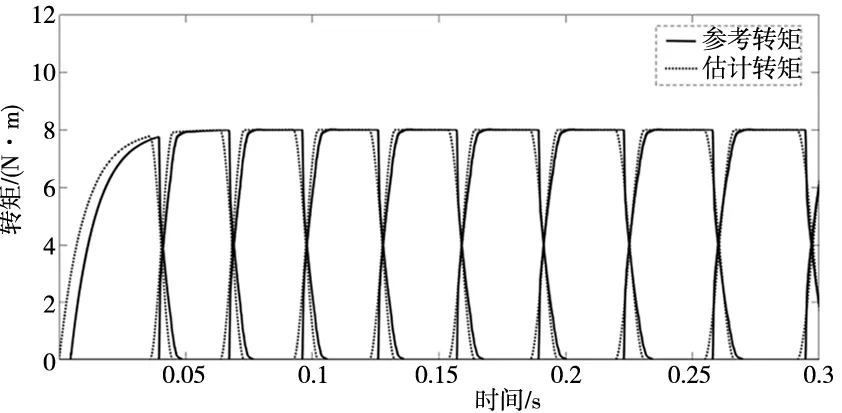

4.3 转矩特性神经网络和BPNN变负载仿真

5 结论
