五轴数控机床非线性误差建模及补偿方法

王艳红，喻伟男，李 冬，崔 悦

(1.沈阳工业大学人工智能学院，沈阳 110870;2.东软医疗系统股份有限公司，沈阳 110167)

0 引言

五轴联动数控机床由刀具和工件的相对运动完成切削动作，适用于加工复杂且高精度的曲面，被广泛应用于装备制造、航空、航天等领域[1]。由于机床在加工过程中需要采用大量的离散直线段逼近工件的轮廓曲线[2]，加之其旋转轴的运动，会造成线性插补与非线性运动之间的不一致而产生非线性误差[3]，从而影响到数控机床的加工精度，因而需要进行有效的补偿和控制。

吴大中等[4]认为非线性误差最大值点位于插补中点处，并根据非线性误差最大值与误差许用值的大小，确定是否在中点处插入新的刀位数据点。该方法需要进行多次判断和选择，算法较为繁琐和耗时。梁全等[5]利用数控系统的RTCP(以刀具旋转中心)和RPCP(以工件旋转中心)功能，根据数控机床类型推导出五轴数控机床的数学模型，并将其应用到五轴数控系统上进行位移的补偿。章永年等[6]利用RTCP编程算法与插补相结合的方式，以减小非线性误差。CUI等[7]通过将刀具刀轴矢量控制在允许的范围内，进而减小非线性误差。该方法优化了数据轨迹，但需要将刀具的最大偏差控制在一定的范围内。

上述研究大多是针对数控机床的特定类型或特殊的编程方式进行处理的，因而应用的门槛较高，且通用性不足。为此，本文提出一种基于误差建模的非线性误差预测和补偿方法，以数控机床的逆运动学模型为基础，通过对插补过程中获得的刀位点误差数据进行辨识，获得误差模型，进而建立误差自适应补偿算法。误差模型辨识和补偿过程具有一定的通用性，有利于提高后置处理算法的精度和使用效率。

1 后置处理及其非线性误差分析

双转台五轴数控机床具有良好的稳定性和加工精度，因而是目前最先进的数控机床。双转台五轴数控机床两个旋转轴都作用在工作台上。机床坐标变换关系如图1所示，OtXtYtZt为与刀具固连的刀具坐标系，OwXwYwZw为与工件固连的加工坐标系，OmXmYmZm为旋转坐标系，在加工坐标系中的位置为rm(mx,my,mz)。

图1 五轴双转台数控机床运动坐标变换关系

数控机床后置处理的主要任务是将CAM 软件生成的刀具轨迹信息转换成机床可执行的程序代码[9]，即根据机床的结构和各轴之间的运动关系，通过逆运动学变换，把图1所示工件坐标系中包含刀具方向矢量和刀具中心位置矢量的刀位数据转化为机床坐标系中数控机床各坐标轴的运动坐标，从而求解出机床三个平动轴X、Y、Z以及两个旋转轴A、C的转动量[9]。

工件加工坐标系中的点坐标值是CAM软件在刀具路径规划阶段根据零件的几何信息进行计算得到的，而机床刀具坐标系中的点坐标值是通过机床各个轴的实际运动解算得到的。由于两种插补方式存在的差异，导致实际刀位运动轨迹会偏离刀位标定的理想轨迹，因而形成了非线性误差。

2 非线性误差建模算法

上述分析可见，后置处理的非线性误差是由数控机床的坐标变换引起的，依赖于数控机床的逆运动学模型和插补运算，因而不易受到异常值扰动的影响，可以运用最小二乘法进行建模。因此，本文提出基于最小二乘法的非线性误差建模算法，其核心思想是，基于模型曲线数据与实际数据之间偏差的平方和为最小的原则，确定拟合非线性误差数据变化趋势的最佳函数。非线性误差建模算法具体包括如下3个步骤。

步骤1：构造非线性误差模型。

设(x,y)为一组观测点，且x=[x1,x2,…,xn]T∈Rn，y=[y1,y2,…,yn]T∈Rn。设所有观测量满足某一拟合曲线函数方程，设为：

y(x)=f(x,ω)

(1)

式中，ω=[ω1,ω2,…,ωn]T为方程的待定参数。为了计算出函数f(x,ω)中参数ω的最优估计值，选取m组观测数据(xi,yi)，(i=1,2,…,m)对该方程进行辨识。m的大小影响拟合曲线的精度，然而若m值过大，会增大计算量。通常可根据实际情况进行选择。

非线性误差是机床旋转轴的运动轨迹与加工路径上直线段之间的偏差，本文通过选取不同的相邻刀位点并对其非线性误差数据进行仿真研究和分析发现，其误差分布呈现先增大后减小的趋势，误差分布形状总体可以用一个二次函数近似，故根据公式(1)建立非线性误差拟合曲线为：

y(x)=ω1x2+ω2x+ω3

(2)

式中，ω=[ω1,ω2,ω3]T，ω1、ω2和ω3为误差拟合函数曲线的待定参数。

步骤2：建立目标函数。

基于最小二乘法的偏差平方和最小原则建立目标函数，使拟合曲线最大化逼近非线性误差的实际变化趋势。为此，选取拟合的目标函数为：

(3)

步骤3：模型参数优化。

设每个非线性误差点位为(xi,yi)，其中i=1,2,…,m。为获得待定参数的最优估计值，建立以下评价函数。

(4)

利用评价函数J*分别对三个参数ω1、ω2和ω3求偏导数，并令其偏导数为零，稍加整理，得到下述三个方程组。

(5)

式中，ai、bi和ci(i=1,2,3)为对J求偏导数时对多项式进行整合得到的数据。对上式求解，便可得到ω=[ω1,ω2,ω3]T，从而得到非线性误差模型的数学表达式。

3 非线性误差补偿算法

误差补偿的目的是通过在非线性误差模型上找到误差最大许用值点所对应的插补点，再进一步得到其它需要重新插入数据点的位置进行误差补偿。将上一节得到的非线性误差模型表达式取为补偿函数，可以方便找到误差的补偿点。

考虑到根据模型计算的误差最大值可以真实地反映出实际加工时工件的精度，而误差最大许用值则表征了加工零件精度的一个最大限制范围，若超出这个范围，可能会使得工件不满足设计要求而不能使用，因此本文给出非线性误差补偿算法的基本规则为：

比较根据模型计算出的误差最大值与误差最大许用值的大小，如果模型的最大值比误差最大许用值大，则进行非线性误差补偿，否则，不进行补偿。

为此，建立非线性误差补偿算法，具体包括如下3个步骤。

步骤1：选取首个插补点。

首先在误差模型曲线上选取任意两相邻数据点X0和X1，并找到非线性误差最大值点，若非线性误差大于所规定的许用值eall，则求出两个与误差许用值对应的插补点位。如图2所示，y(x)为上一节得到误差二次型曲线，为便于描述，取X0为坐标点(0,0)、X1为坐标点(1,0)，emax为误差最大值点。因

emax>eall

(6)

则根据误差模型，计算与误差许用值所对应的两个点xe1和xe2。

由于X0到xe2之间距离较长，为了防止期间在加工时所产生的非线性误差最大值仍大于误差最大许用值，本文沿加工方向，选取靠近X0的xe1作为首个插补点。

图2 误差许用值最大值点位置示意图

步骤2：确定其他待补偿点位。

确定第一个插补点后，通过计算选取其他的插补点进一步进行误差补偿。设补偿点位的个数δ，有：

(7)

按照式(6)，将括号内计算的值进行向下取整得到的δ值。

于是，得到所有需补偿点位xi，即：

xi=X0+(xe1-X0)i(i=1,2…,δ)

(8)

(9)

Pi=Pk+β|Pe-Pk|i(i=1,2,…,δ)

(10)

式中，Pi为相邻两个刀位数据点之间所有需要插入的新的刀位数据点；β为相邻两个刀位数据点的方向矢量；Pk为相邻两个刀位数据点的前一个刀位数据点；Pk+1为相邻两个刀位数据点的后一个刀位数据点；Pe为误差许用值点所处位置的第一个新插入的刀位数据点。

步骤3：完成误差补偿。

将得到的新的插补点Pi通过正向运动学变换计算得到新的刀位数据点插入到两个数据点之间，通过后置处理算法将新的刀位数据点文件转换成NC代码。

通过误差补偿，所产生的非线性误差最大值均小于误差最大许用值，满足工件的加工精度要求。

4 仿真研究与分析

为了验证所提出误差建模与误差补偿算法的有效性，选取文献[10]中实际加工刀位数据点数据进行仿真研究。

4.1 非线性误差建模算例仿真

任意选取两个相邻刀位点X0(P0,U0)和X1(P1,U1)，其中，Pi为其在工件坐标系中的刀具位置；Ui为刀轴矢量，如表1[10]所示。

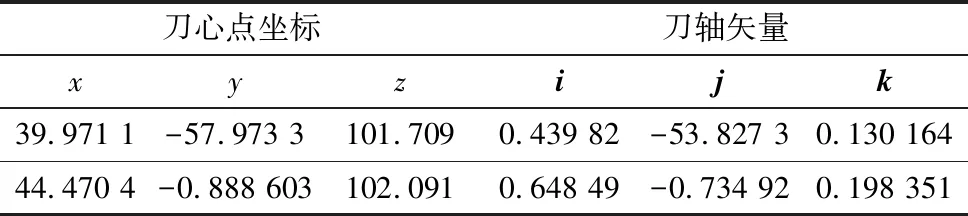
表1 两个相邻刀位点数据

如表2所示，不失一般性，本文将理想轨迹设为一条直线，非线性误差被看作实际的刀位轨迹到直线的误差。

表2 非线性误差 (mm)

根据上述点位得到相应的非线性误差模型的数学表达式。

将上述点位在MATLAB环境下进行仿真如图3所示，给出了经过非线性误差补偿前后以及理想轨迹曲线，其中直线为补偿前轨迹，虚线为理想轨迹，点划线为补偿后的轨迹，如图4所示为两点间进行非线性误差补偿前后的曲线分布图。

图3 三维补偿仿真结果

图4 两点间非线性误差仿真图

上述算例仿真结果表明，本文选择二次函数对非线性误差进行拟合是可行的，并且只需要一次计算就对非线性误差补偿完成，不需要再次对其进行补偿。此外，根据补偿前后的误差比较说明，本文给出的非线性误差补偿方法，能够基于插补算法计算获得的数据建立起误差补偿的模型。

4.2 非线性误差补偿实例仿真

根据加工点位数据，首先通过后置处理以及插补函数计算出每两点之间的插补点位以及所对应的非线性误差，再建立非线性误差模型，进一步采取第3章节非线性误差补偿机制，对非线性误差进行补偿和补偿。补偿前后以及理想轨迹图如图5所示。将图5轨迹图进行局部放大得出图6。其中，直线为通过本文算法补偿后的轨迹，点划线为未补偿的轨迹曲线，虚线为理想轨迹，从中可以看出经过补偿之后的曲线更加接近理想的轨迹曲线。

由仿真结果表明，采用误差补偿机制之后的加工轨迹更加贴合理想轨迹。

图5 刀位数据非线性误差仿真图

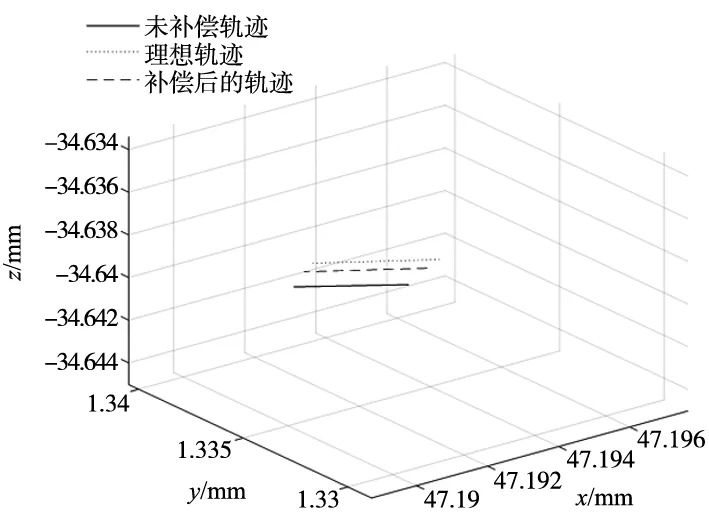
图6 轨迹局部放大图

如表3所示，给出了补偿前后部分非线性误差数据比较，表明所提出的通过对误差模型建模以及对其补偿的方法，能够有效减少非线性误差，提高工件的加工精度。

表3 补偿前后非线性误差数据(部分)

5 结论

针对五轴数控机床所产生的非线性误差，提出基于最小二乘法的非线性误差建模算法，建立的非线性误差补偿机制，并通过仿真验证，表明实际加工出来的轨迹相比于补偿前更加贴合理想的轨迹，验证了所提出非线性误差补偿方法的可行性和有效性。利用本文所提出方法，可以只需要一次计算就对非线性误差补偿完成，不需要多次循环计算。此外，所提出误差建模和补偿算法只与误差数据有关，因而理论上可以适用于任意数控机床非线性误差的建模，经适当变化可应用于其他类型的数控机床，具有较好的可移植性。