巡检机器人机械臂空间变形解析模型分析*
2022-03-04王琬琪张世轩徐志刚尚东阳
王琬琪,张世轩,徐志刚,周 淦,尚东阳
(1.中国科学院沈阳自动化研究所,沈阳 110016;2.中国科学院机器人与智能制造创新研究院,沈阳 110169;3.华北计算机系统工程研究所,北京 100083;4.中国科学院大学,北京 100049;5.东北大学机械工程与自动化学院,沈阳 110819)
0 引言
近年来随着机器人、人工智能、图像识别等技术的不断发展,特种作业机器人取得了长足的进步。输电线路巡检机器人属于特种作业机器人研究的前沿领域[1-2]。在国外,输电线路巡检机器人的研究始于上世界80年代,日本东京电力公司最先开展了巡线机器人的研究,在1988年开发出了第一台样机——光纤复合架空地线(OPGW)巡检移动机器人[3]。近年来,研究单位研制了多种作业工具,不仅能够完成线路的在线检测,还能够对故障进行及时维护[4]。加拿大、美国、英国等西方发达国家也陆续开展对于巡线机器人的研究,已经研发出了具有跃障、爬坡功能的巡线小车。进入21世纪后,随着研究的不断深入,巡检机器人由小车形式逐渐发展为具有移动轮、重心调节箱的关节臂形式。日本关西电力公司和东京工业大学的科研人员联合研制出了Expliner电力机器人[5-6],加拿大魁北克水电研究院研制了带电导线上巡检的机器人-LineScout[7],美国电力研究院(EPRI)通过机器人与输电线路环境的一体化设计研制了一条被动式自主越障巡检机器人TI[8],加州大学圣地亚哥分校(UCSD)雅各布斯工程学院研制了一种悬摆式移动机器人“SkySweeper”[9]。
相比于国外,我国对于线路巡检机器人的研究起步较晚。20世纪90年代末,国内很多大学及研究所相继展开了高压输电线路巡检机器人的研究。1997年武汉大学设计出了具有自动越障功能的高压输电线路巡线小车[10]。在国家“十五”863计划的资助下,中科院沈阳自动化研究所研发的一种变距越障巡检机器人[11],而武汉大学则展开了220 kV的高压输电线路巡检机器人的研究[12]。
目前对于输电线路巡检机器人的研究主要是机器人的结构设计、运动学分析等[13-14],但鲜有进行机器人变形的研究。由于输电线路巡检机器人属于串联关节臂形式,在机器人运动过程中其末端手爪存在变形,该种变形可能会对输电线路造成损伤。因此对机器人进行静力变形的分析显得尤为重要。
本文在完成线路巡检机器人的结构设计基础上,首先通过建立机器人的运动学模型,求得了机器人的雅可比矩阵;进而建立了机器人的柔度矩阵、分析了末端手爪变形量;最后通过仿真得到了4条反解路径与机器人末端最大变形量的曲线图,可选择出最佳反解路径。
1 机器人连杆坐标系的建立
本文将线路巡检机器人双臂运动分解成若干个单臂运动,以单臂为研究对象,根据D-H法建立巡检机器人连杆坐标系。输电线路巡检机器人连杆坐标系如图1所示,相应的连杆参数如表1所示。

图1 输电线路巡检机器人整机结构简图与坐标系

表1 输电线路巡检机器人连杆参数表

这些子变换都是相对于动坐标系描述的,按照“从左到右”的原则可以得到:
(1)
式中,Rot(x,αi-1)表示绕x轴旋转αi-1角;Trans(x,ai-1)表示沿x轴移动ai-1距离;Rot(z,θi)表示绕z轴旋转θi角;Trans(z,di)表示沿z轴移动di距离。
得到连杆变换公式:
(2)

根据变换传递公式:
(3)
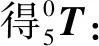
(4)
至此建立了线路巡检机器人连杆坐标系及连杆变换矩阵,通过式(4)可以求得机器人末端执行器的位姿变化。
2 机器人雅可比矩阵的推导
雅可比矩阵既是研究操作空间速度与关节空间速度的线性映射关系,也可以表示操作空间外力与关节空间内力的线性映射关系。在研究机器人变形量前,需要求得机器人操作臂的雅可比矩阵。雅可比矩阵的求解方法主要有微分变化法、矢量积法两种方法。课题组采用微分变化法求得输电线路的雅可比矩阵。

J(q)=[J1(q)J2(q)J3(q)J4(q)J5(q)]
(5)
以J1(q)为例说明雅可比矩阵的组成。
3 机器人变形模型的建立
机器人末端操作臂的终端在外力作用下会产生变形。变形的大小与操作臂的刚度以及作用力的大小有关。因此操作臂的刚度是影响机器人动态性能和定位精度的主要因素。产生变形的部位有连杆本身、连杆支撑和关节驱动装置。
3.1 操作臂刚度矩阵
机器人产生变形的部位有:连杆本身、连杆支撑和关节驱动装置。对于串联关节臂形式的机器人,末端操作臂主要的变形是源自连杆产生的变形。机器人的总变形量取决于各个关节的变形量,并且每个连杆的变形量也各不相同。为研究方便,将整个机器人系统的刚度用操作臂刚度矩阵Kq表示,Kq由各个连杆的刚度kqi表示,如式(6)所示,式中kqi表示连杆i的弹簧刚度系数。
(6)
组成输电线路巡检机器人的各个连杆均是不规则物体,所以按照刚度公式计算刚度比较困难。由刚度概念可知:刚度是指材料或结构在受力时抵抗弹性变形的能力。在宏观弹性范围内,刚度是零件荷载与位移成正比的比例系数,即引起单位位移所需的力。根据柔度定义易知刚度是单位力作用下引起变形位移的倒数。故可得到机器人连杆刚度的表达式为:
(7)
式中,δi为施加单位力后连杆i的变形量。
在有限元分析软件ANSYS中依次对线路巡检机器人的各个连杆沿运动方向施加单位力,利用软件测量其变形量,并取其倒数,进而得到各个连杆的刚度,结果如表2所示。
根据表2得到连杆刚度kqi,将其代入式(6)中可得到操作臂的刚度矩阵。

表2 机器人连杆刚度表
3.2 操作臂末端柔度矩阵
操作臂末端柔度矩阵C(q),用以表示操作空间的力F与变形矩阵D之间的线性联系。C(q)是一个m×m的对称方阵,它与雅可比矩阵有关,表达式如式(8)所示。由于雅可比矩阵随操作臂的形位而变化,因此C(q)也与形位有关。
(8)
将雅可比矩阵J(q)、操作臂的刚度矩阵Kq带入式(8)中,求得线路巡检机器人操作臂末端柔度矩阵C(q)的表达式为:
(9)
式中,以C11的表达式为例,说明机器人操作臂末端柔度矩阵的组成。
3.3 末端变形量求解
根据刚度定义,可以根据连杆刚度和连杆变形量计算连杆间的广义关节力:
τ=Kqdq
(10)
式中,τ是关节力矩;dq是关节变量由于τ产生的变形。
忽略重力和关节摩擦力的影响,根据末端外界作用力F即可得到等效的关节力矩,有:
dq=KqJT(q)F
(11)
式中,J(q)为操作臂的雅可比矩阵(m×n阶);F为m维的操作力(外界作用力)矢量。
变形量与雅可比矩阵的联系由微分运动关系确定:
D=J(q)dq
(12)
式中,D为末端变形量。
联立式(8)、式(10)~式(12)即可求得变形量与外力F的联系:
(13)
式中,建立了变形量D与外力F的表达式。
3.4 最大变形量的求解
输电线路巡检机器人位于某一形位时,单位操作力引起的变形大小与作用力的方向有关。最大变形和最小变形所对应的方向称为变形主轴。变形的模方为:
DTD=FTC(q)TC(q)F
(14)
又因为单位力F满足条件为:
DTD=FTC(q)TC(q)F
(15)
因此最大、最小变形量问题转化为:在单位力满足约束方程的条件下,求解以变形的模方为目标函数的条件极值问题。引入拉格朗日乘子λ,定义拉格朗日函数L。
L=DTD-λ(FTF-1)
(16)
条件极值的必要条件为:
(17)
根据式(17)可知,拉格朗日乘子λ即为平方柔度矩阵CT(q)C(q)的特征值,最大、最小柔度对应方向即为特征向量方向,最大与最小变形量即为:

(18)
式中,κmax为最大特征值,κmin为最小特征值。
4 模型验证及应用
4.1 模型的验证
输电线路巡线机器人各杆长参数与位置参数如表3所示,根据式(9)可求得操作臂末端柔度矩阵C(q),再求出CT(q)C(q)的特征值为:
κ1=4.280 3×10-16、κ2=9.167 6×10-17、
κ3=7.853 7×10-18、κ4=1.574 4×10-10、
κ5=3.036 4×10-10、κ6=1.690 5×10-8
将最大、最小特征值带入式(18)计算最大变形量为1.300 2×10-4mm。

表3 连杆参数表
利用ANSYS软件在机器人末端添加单位力后测得机器人的最大变形量为1.225 5×10-4mm,结果如图2所示。与计算结果基本一致,验证了所建立的机器人变形模型的正确性。

图2 输电线路巡检机器人受力变形图
4.2 基于变形模型的路径选择
通过解逆运动学求得输电线路巡检机器人的反解共有8组,选择其中4组合理的反解,如表4所示。

表4 反解参数表
应用操作臂末端柔度矩阵与机器人单位力作用下最大变形量公式,求解上述4种反解路径的最大变形量,并选择变形量最小的路径。首先将每条路径划分为若干个间距相等的点,并获得巡检机器人末端执行器占据这些点时机器人连杆坐标系的参数。将参数代入式(9)、式(18)中即可得到各个点在单位力作用下的最大变形量。将每条路径各个空间点所对应的最大变形量进行整理,如表5所示。
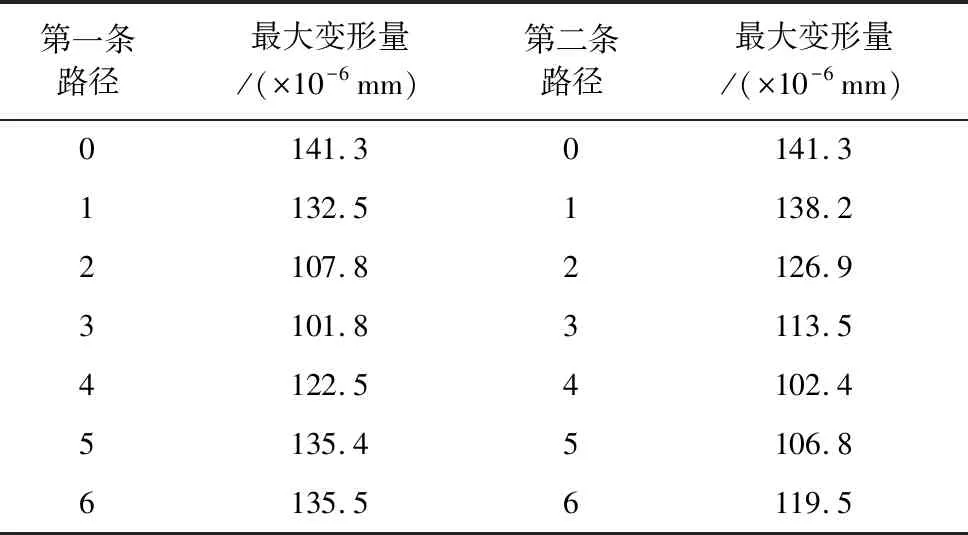
表5 反解路径空间点最大变形量
将4条反解路径中的各个空间点所对应的最大变形量通过多项式插值拟合,得到4条反解路径与机器人末端最大变形量的曲线图,如图3所示。

图3 反解路径最大变形图
对反解路径中最大变形量关系的仿真表明,第2条路径所在空间点在单位力作用下的变形量最小,机器人末端形变量峰值最小,第2条路径抗干扰能力最佳。同时,反解路径差值拟合结果也证明了文章所建立的变形解析模型的正确性。
5 结论
本文一种线路巡检机器人的结构设计基础上,对巡检机器人机械臂空间变形解析模型进行了建立与应用研究。通过相关计算仿真,得到以下结论:
(1)建立了单位力作用下的机械臂末端变形量表达式。文章基于巡检机器人的操作臂刚度矩阵、操作臂末端柔度矩阵,建立了输电线路巡线机器人的变形解析模型。通过ANSYS软件仿真计算出巡检机器人末端执行器在单位力作用下的最大变形量,从而验证了输电线路巡检机器人变形模型的正确性。
(2)通过建立的变形解析模型求解了最佳反解路径。通过对选取的4种反解路径所在空间点的最大变形量进行仿真计算,通过拟合曲线仿真,可见第2条路径变形量最小,对反解路径进行了有效筛选。
(3)建立的机械臂空间变形解析模型具有一般性。文章所建立的机械臂末端形变量模型在后续研究中可应用到其他类型机器人中,可对机器人运动控制过程的干扰力有效分析,提高控制精度。
