基于流固耦合的压气机叶片拓扑优化研究*
2022-03-04罗庆怡胡晓兵李何钰秋
罗庆怡,梅 琦,胡晓兵,李何钰秋
(1.四川大学机械工程学院,成都 610065;2.宜宾四川大学产业技术研究院,宜宾 644000)
0 引言
离心式压气机因其体积小、单级增压比高等优点被广泛运用于航空发动机、船舶燃气轮机等[1]。压气机叶片在高转速工况下不仅受到气流载荷和离心力,同时还要承受气动载荷与其力耦合作用下的振动载荷,进而发生不同程度的颤振现象,导致叶片产生疲劳破坏甚至断裂,严重影响压气机的工作性能[2]。因此,对压气机叶片在各种场耦合作用下的应变及动频研究及优化显得格外重要。
SUBRAMANI等[3]采用了有限元法对叶轮进行应力仿真,结果表明随着旋转速度越高,离心力作用越明显,应力越大,叶轮背面所受应力较大。张磊等[4]总结了流固耦合的基本理论及控制方程,对叶轮机械流固耦合问题进行了研究,完整介绍了流固耦合理论体系。王征等[5]基于计算流体力学与计算结构力学的耦合算法研究了压气机叶片的流固耦合特性及颤振特性,为压气机稳定性的判定提供重要依据。李存程等[2]以整体式轴流压气机叶片为对象,采用流固耦合方法求解得到叶片压力、应变及模态,并对叶片前缘和尾缘采用变半径设计,有效提高了固有频率并同时削减了振动。王佳利等[6]以压气机为对象,通过改变叶片出口段沿旋转的方向的倾斜角度改善了叶轮内流动情况并改善了叶片压力分布。张敏等[7]总结归纳了流体拓扑优化的数学模型、流动控制方程及求解方法,对比传统形状与尺寸设计得到流体拓扑优化一系列的优良特性,为拓扑优化这种优化方式在叶轮机械中的运用打下了基础。
综上所述,国内外大多数研究者对压气机叶片的研究主要集中在叶片流固耦合理论分析以及叶片的部分尺寸参数优化上,没有较为全面地对叶片整体结构进行优化,对于具有更多设计自由度的拓扑优化方法的应用研究较为欠缺。基于ANSYS Workbench与CFX仿真平台运用流固耦合方法,对压气机叶片进行数值模拟,重点采用多目标拓扑分析方法,在不涉及具体结构尺寸情况下对叶片进行研究,提高叶片优化分析效率,为压气机叶片的优化提供了思路。
1 计算流程
采用单向流固耦合方法进行计算。具体流程为:①建立叶片几何模型;②流场网格与叶片网格划分;③流场网格模型导入CFX进行流场计算;④流场结果传递至结构场进行耦合求解;⑤通过GENESIS对耦合结果进行多目标拓扑分析;⑥重建模型进行计算。对离心式压气机叶片分析求解流程如图1所示。
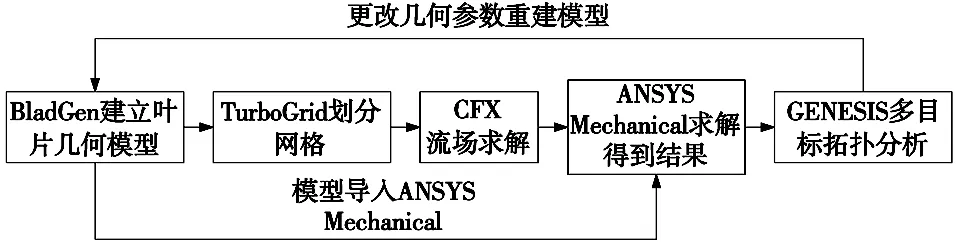
图1 计算流程
2 流固耦合理论
流固耦合方法的基本原理是流体与固体的交界面处满足位移d、应力τ、热流量φ和温度T等变量相等或满足守恒定律[2]。其中流体遵循流动控制方程;固体遵循固体控制方程。
2.1 流动控制方程
叶轮单流道内流体遵循质量、动量与能量方程[8]。
质量守恒方程:

(1)
式中,ρ为流体密度,kg/m3;t为时间,s;u为速度矢量。
动量守恒方程:
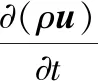
(2)
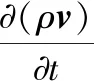
(3)
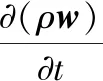
(4)
式中,u、v、w分别为速度矢量在x、y、z方向的分量;μ为动力粘度,Pa·s;Su、Sv、Sw为动量守恒方程的广义源项。
能量守恒方程:
(5)
式中,cρ为流体比定压热容,J/(kg·K);T为流体温度,K;k1为流体传热系数,W/(m·K);ST为粘性耗散项。
2.2 固体控制方程
通过牛顿第二定律得出:
ρsds=·σs+fs
(6)
式中,ρs为固体密度,kg/m3;σs为柯西应力张量;fs为体积力矢量;ds为固体域当地加速度矢量。
2.3 流固耦合方程
流固耦合基本原理亦满足守恒定律,即:
(7)
式中,τ为应力,Pa;d为位移,m;Φ为热流量,W;T为温度,K;下标f表示流体;s表示固体。
3 叶片有限元模型建立
3.1 叶片流场模型建立
利用ANSYS Workbench中的BladeGen模块对压气机叶片进行三维建模,叶片几何参数如表1所示,材料选用钛合金铝。网格设置采用专业网格划分软件TurboGrid完成,TurboGrid对旋转类机械网格划分效率高,速度快[9]。叶片网格划分模型如图2所示。网格节点数为257 812;单元数为233 132。

表1 叶片几何参数

图2 流场网格划分模型
3.2 叶片有限元模型建立
采用六面体单元进行网格划分,网格模型如图3所示。网格节点数为27 543,节点个数为5280。

图3 叶片网格划分模型
4 模型计算
4.1 叶片流场分析
采用ANSYS CFX对叶片流场模型进行计算,将TurboGrid中的网格数据导入到CFX中,定义进口、出口以及壁面。计算模型采用Shear Stress Transport(剪切应力湍流传输模型),壁面和叶轮表面均采用绝热无滑移条件。为能达到收敛精度并提高计算可信度,边界条件采用进口总压与出口平均静压[10]。进口边界总压为101 325 Pa,通过逐渐增大出口背压改变流量来逼近失速点,失速前的最后一个收敛解作为失速边界点[11]。CFX求解器残差控制值设置为0.000 01,最大迭代步数设置为1000,流场模型边界定义如图4所示。

图4 模型边界条件示意
叶片在额定转速条件下的压力分布如图5所示。压力最大位置主要分布在进口处,由于叶片进口处离旋转轴较远,线速度较大,因此压力分布由叶片进口处到叶片出口处呈逐渐减小的趋势。
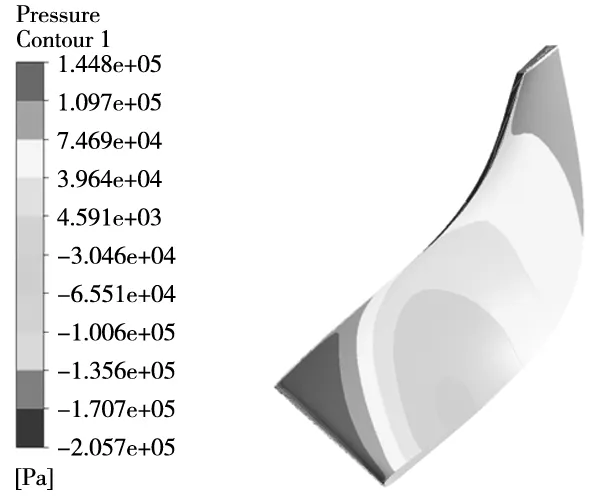
图5 叶片流场压力分布
4.2 叶片耦合场分析
通过对叶片施加流场压力,编辑叶片材料后得到真实的叶片应力与应变。将叶片的流场压力导入ANSYS Workbench中,对叶片根部施加固定约束,定义旋转速度以完成流固耦合设置,并进行计算得到结果。叶片最终应变与应力分别如图6和图7所示。从结果可得到,叶片应变量从叶顶至叶根逐渐减小,进口处叶顶应变量最大为0.209 5 mm;叶片根部的应力较叶顶大,进口处叶根的应力最大为767.81 MPa。由于进口处叶根与叶顶的厚度较小,可认为应力应变对两处的影响较大。

图6 耦合场应变分布 图7 耦合场应力分布
5 叶片拓扑分析
5.1 GENESIS模块介绍
GENESIS是一个将有限元求解器和高级优化算法基于一体的结构优化软件,主要用于结构轻量化和拓扑优化设计。GENESIS优化模型的构建基于高级近似概念方法,可以快速可靠地进行优化迭代,计算效率高,所需优化迭代次数更少。
5.2 基于Genesis的拓扑流程
(1)将以上耦合场分析模型输入到GENESIS模块,GENESIS中约束边界条件将与模态分析中边界条件保持一致;
(2)定义优化设计变量和目标函数。每个单元的材料密度即为设计空间中的设计变量,将叶片设计空间应变与应力最小作为目标函数,并将该目标函数的数值限制在一个区间内。假设叶片需要单元数为m,第i个单元密度表示为ρi(i=1,2,…,m),以ρ={ρ1,ρ2,…,ρm}T为设计变量。叶片的多目标优化函数设为F(ρ),w是其中一个目标函数的权重,本次优化权重w取0.5。C1(ρ)为第1次设计周期后的该目标函数值,Ci(ρ)为第i次设计周期后的该目标函数值,γ1(ρ)为第1次设计周期后的另一目标函数值,Ci(ρ)为第i次设计周期后的该目标函数值。定义约束方程Fj(ρ),j为约束个数,则叶片拓扑模型表示[3]:
(8)
式中,Sj、Qj为约束条件上下限。
(3)定义优化空间。设置叶片整体为待优化区域。
(4)求解叶片拓扑模型并查看结果,其中模型求解目标函数迭代曲线如图8所示,约束波动迭代曲线如图9所示。

图8 目标函数迭代曲线 图9 约束波动迭代曲线
GENESIS默认迭代步数为15步,如图8和图9所示,第10步即完成了优化目标。叶片拓扑优化密度云图如图10所示,同时,GENESIS对拓扑优化后的模型进行重建,如图11所示。其中,颜色偏深蓝色的区域为建议去除部分,颜色偏深红色的区域为建议保留部分,颜色介于两色之间的区域可去除亦可保留。

图10 拓扑优化密度云图 图11 拓扑优化模型效果图
5.3 拓扑优化改进
由图10可知,叶片重建模型的叶顶与叶轮出口后缘减少了部分材料。根据以上拓扑优化结果,在不改变叶轮进出口直径的条件下,主要改进措施为:在不修改叶轮进出口的直径情况下,适当增加叶顶的弧度并降低叶片出口的高度。通过BladeGen对叶片子午面参数进行修改,如图12所示。依次将叶片出口高度减小1 mm和2 mm,并同时增加了叶顶的弧度;特别地,在叶片进口高度减小1 mm的基础上,再增加一组对照,增加一定量的弧度,并与未增加前进行对比。
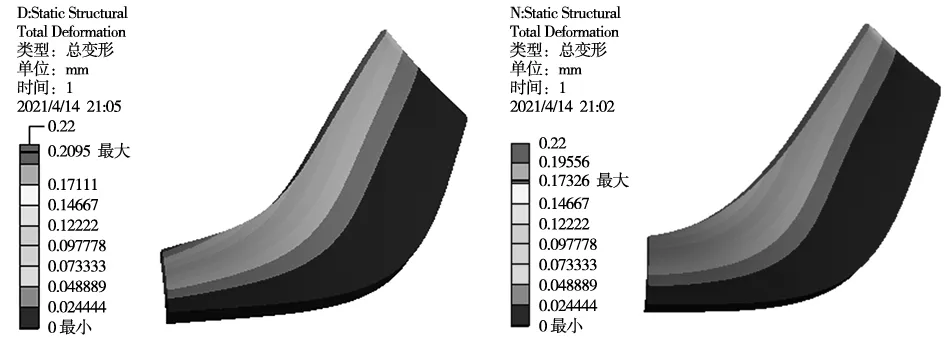
(a) 出口叶片高度10 mm时应变 (b) 出口叶片高度9 mm时应变

(c) 出口叶片高度8 mm时应变 (d) 出口叶片高度9 mm同时增加弧度时应变图12 优化后叶片耦合场应变图
6 重建模型并进行流固耦合分析
通过多目标拓扑优化,重新建立叶片模型并重复以上的流固耦合分析流程,优化后应变如图13所示。随着叶片出口高度降低,叶片的应力应变明显降低,应变主要集中在叶顶中间厚度较厚部分,应力集中在叶根出口,在叶片出口高度同为9 mm的情况下,适当增加叶顶弧度后,应变下降率从17.1%增至25.5%;应力下降率从13.9%增至25%。可以看到优化后的叶片模型性能明显提升,验证了拓扑分析的正确性。拓扑优化结果如表2所示。
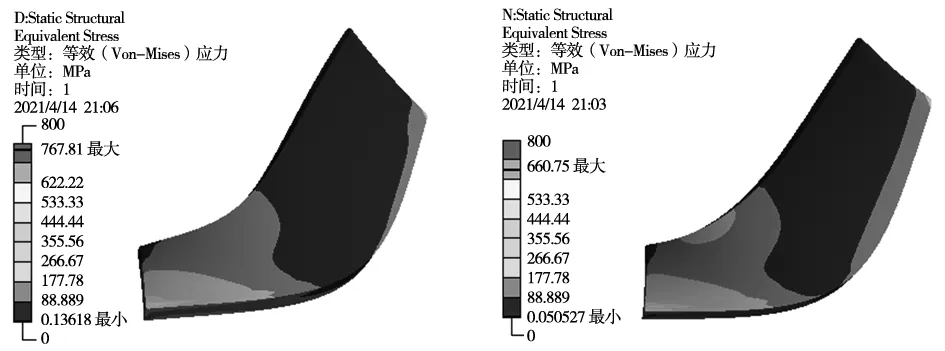
(a) 出口叶片高度10 mm时应力 (b) 出口叶片高度9 mm时应力
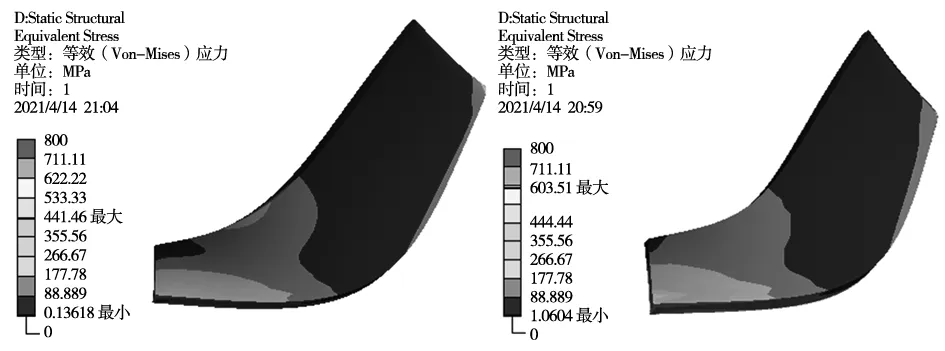
(c) 出口叶片高度8 mm时应力 (d) 出口叶片高度9 mm同时增加弧度时应力图13 优化后叶片耦合场应力图

表2 拓扑优化前后参数对比
7 结论
通过ANSYS Workbench仿真平台对离心式压气机叶片进行单向流固耦合仿真分析,并在GENESIS模块下进行多目标拓扑优化,得到以下结论:
(1)使用拓扑优化方法对叶片结构的应力和应变进行多目标优化。优化结果和重建模型后的有限元验证结果表明,降低叶片出口高度并增加叶顶弧度,应变主要集中在叶顶中间厚度较厚部分,整体应力和应变值得到显著降低。
(2)此外,本研究提出的叶片拓扑优化方法可仅根据已知边界条件与载荷条件,在不涉及结构参数化建模的条件下提供更优的结构设计方案。该特性避免了对复杂形状结构部件的参数化建模的困难,提升了优化设计效率,在叶片结构优化方面具有可行性。
